Sujet de métropole, juin 2019, exercice 6

Énoncé

17 points

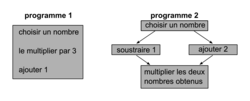
Voici deux programmes de calcul.

Vérifier que si on choisit 5 comme nombre de départ,

• le résultat du programme 1 vaut 16 ;

• le résultat du programme 2 vaut 28.

Faites attention à détailler vos calculs, et vérifiez vos résultats avec votre calculatrice.

On appelle A(x) le résultat du programme 1 en fonction du nombre x choisi au départ.

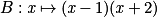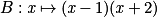La fonction $B:\textit{x} \mapsto (\textit{x}-1)(\textit{x}+2)$ ) donne le résultat du programme 2 en fonction du nombre x choisi au départ.

a) Exprimer A(x) en fonction de x.

Il faut appliquer le programme 1 en choisissant x comme nombre de départ au lieu de choisir un nombre donné.

b) Déterminer le nombre que l'on doit choisir au départ pour obtenir 0 comme résultat du programme 1.

Il faut remonter le programme 1 à l'envers, car on a le résultat final. On fait les opérations du programme à l'envers ou alors on trouve le nombre x initial en faisant une équation.

Développer et réduire l'expression : B(x) = (x − 1)(x + 2).

Vous devez faire un double développement, donc il faut penser à bien effectuer les quatre opérations. Et ensuite pour réduire, vous devez regrouper les termes qui se ressemblent.

a) Montrer que B(x) − A(x) = (x + 1)(x − 3).

À partir des expressions B(x) et A(x), il faut réduire B(x) − A(x). L'expression obtenue est difficile à factoriser donc il est préférable de développer le membre de droite et de le comparer avec l'expression obtenue précédemment.

b) Quels nombres doit-on choisir au départ pour que le programme 1 et le programme 2 donnent le même résultat ? Expliquer la démarche.

Il faut trouver le nombre x du départ pour que les expressions des deux programmes soient égales. Pensez à utiliser la question 4. a) pour votre résolution.

Corrigé

Avec le programme 1 : on choisit 5 ; on multiplie par 3 : 5 × 3 = 15 ; on ajoute 1 : 15 + 1 = 16. Donc avec le programme 1, on obtient bien 16 en prenant 5 au départ.Avec le programme 2 : on choisit 5 ; on soustrait 1 : 5 − 1 = 4 et en même temps on ajoute 2 : 5 + 2 = 7 ; on multiplie les deux résultats obtenus 4 × 7 = 28. Donc avec le programme 2, on obtient bien 28 en prenant 5 au départ.

a) En prenant x comme nombre de départ, on le multiplie par 3, puis on ajoute 1, on obtient alors : A(x) = 3x + 1.

b) On veut que le résultat du programme 1 soit égal à 0. Le programme 1 correspond à la formule A(x) = 3x + 1. On cherche donc x pour que : A(x) = 3x + 1 = 0.
On résout l'équation 3x + 1 = 0.
On soustrait 1 dans chaque membre de l'équation : 3x = − 1.
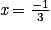On divise par 3 dans chaque membre : $\textit{x}= \frac{-1}{3}$ .
Donc pour obtenir 0 avec le programme 1, il faut choisir au départ le nombre $\frac{-1}{3}$ .

B(x) = (x − 1)(x + 2)
B(x) = x × x + x × 2 − 1 × x − 1 × 2
B(x) = x² + 2x −1x − 2
B(x) = x² + 1x − 2.

a) B(x) − A(x) = x²+ 1x − 2 − (3x + 1)
B(x) − A(x) = x²+ 1x − 2 − 3x − 1
B(x) − A(x) = x² − 2x − 3
et (x + 1)(x − 3) = x × x − 3 × x + 1 × x −3 × 1
(x + 1)(x − 3) = x² − 3x + 1x − 3 = x² − 2x − 3.
Donc : B(x) − A(x) = (x + 1)(x− 3).

b) Si on veut que les deux programmes donnent le même résultat pour un nombre de départ, cela signifie qu'on cherche x pour que : B(x) = A(x), c'est-à-dire pour que : B(x) − A(x )= 0.
On doit donc résoudre : (x + 1)(x − 3) = 0, c'est une équation produit nul.
Il y a deux solutions possibles : x + 1 = 0 ou x − 3 = 0.
On obtient donc : x = −1 ou x = 3.
Les deux nombres possibles à choisir pour que les programmes donnent le même résultat sont −1 et 3.

Sujet de métropole, juin 2019, exercice 6

Énoncé

Annexes

Corrigé