Énoncé
18 points
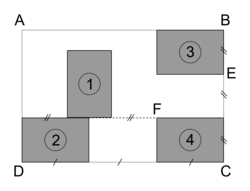
Olivia s'est acheté un tableau pour décorer le mur de son salon. Ce tableau, représenté ci-après, est constitué de quatre rectangles identiques nommés (1), (2), (3) et (4) dessinés à l'intérieur d'un grand rectangle ABCD d'aire égale à 1,215 m2. Le ratio longueur : largeur est égal à 3 : 2 pour chacun des cinq rectangles.
 |
1. Recopier, en les complétant, les phrases suivantes. Aucune justification n'est demandée.
a) Le rectangle … est l'image du rectangle … par la translation qui transforme C en E.
b) Le rectangle (3) est l'image du rectangle … par la rotation de centre F et d'angle 90° dans le sens des aiguilles d'une montre.
c) Le rectangle ABCD est l'image du rectangle … par l'homothétie de centre … et de rapport 3.
Il faut connaître les idées les plus importantes pour chacune des transformations.
La translation, c'est faire glisser une figure dans une certaine direction.
La rotation, c'est faire tourner une figure autour d'un point, avec un certain angle.
L'homothétie, c'est reproduire la figure initiale avec un coefficient d'agrandissement ou de réduction et en éloignant ou en rapprochant la figure par rapport au centre donné.
La translation, c'est faire glisser une figure dans une certaine direction.
La rotation, c'est faire tourner une figure autour d'un point, avec un certain angle.
L'homothétie, c'est reproduire la figure initiale avec un coefficient d'agrandissement ou de réduction et en éloignant ou en rapprochant la figure par rapport au centre donné.
2. Quelle est l'aire d'un petit rectangle ?
Pensez à utiliser le coefficient d'agrandissement entre le rectangle ABCD et les petits rectangles que vous avez trouvé à la première question. Attention : lorsque le coefficient des longueurs est k, le coefficient d'agrandissement des aires est k2.
3.
Quelles sont la longueur et la largeur du rectangle ABCD ?
Utilisez le ratio entre la longueur et la largeur pour ne pas avoir deux mesures inconnues, mais une seule et l'autre qui en dépend.
À partir de ce lien, et en utilisant le résultat de l'aire du rectangle ABCD, vous pouvez obtenir une équation qui vous permettra de trouver la valeur de la largeur du rectangle.
Enfin, il faut en déduire la longueur du rectangle à partir du ratio initial.
À partir de ce lien, et en utilisant le résultat de l'aire du rectangle ABCD, vous pouvez obtenir une équation qui vous permettra de trouver la valeur de la largeur du rectangle.
Enfin, il faut en déduire la longueur du rectangle à partir du ratio initial.
Corrigé
1.
a) Le rectangle (3) est l'image du rectangle (4) par la translation qui transforme C en E.
b) Le rectangle (3) est l'image du rectangle (1) par la rotation de centre F et d'angle 90° dans le sens des aiguilles d'une montre.
c) Le rectangle ABCD est l'image du rectangle (2) par l'homothétie de centre (D) et de rapport 3.
Ou : Le rectangle ABCD est l'image du rectangle (4) par l'homothétie de centre (C) et de rapport 3.
Ou : Le rectangle ABCD est l'image du rectangle (3) par l'homothétie de centre (B) et de rapport 3.
Ou : Le rectangle ABCD est l'image du rectangle (4) par l'homothétie de centre (C) et de rapport 3.
Ou : Le rectangle ABCD est l'image du rectangle (3) par l'homothétie de centre (B) et de rapport 3.
2. Comme le rapport de l'homothétie pour passer d'un petit rectangle au rectangle ABCD, cela signifie que les longueurs des petits rectangles sont multipliées par 3 pour obtenir celles du rectangle ABCD. À l'inverse, on doit diviser par 3 les longueurs du rectangle ABCD pour obtenir les longueurs des petits rectangles.
Et donc pour les aires, il faut diviser l'aire du rectangle ABCD par 32 = 9 pour obtenir l'aire d'un petit rectangle.
Apetit rectangle = AABCD ÷ 9 = 1,215 ÷ 9 = 0,135 m2.
L'aire d'un petit rectangle est donc de 0,135 m2.
Et donc pour les aires, il faut diviser l'aire du rectangle ABCD par 32 = 9 pour obtenir l'aire d'un petit rectangle.
Apetit rectangle = AABCD ÷ 9 = 1,215 ÷ 9 = 0,135 m2.
L'aire d'un petit rectangle est donc de 0,135 m2.
3. Comme on sait que le ratio entre la longueur et la largeur est 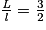 , alors
, alors 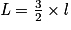 .
.
Avec l'aire du rectangle ABCD, on obtient :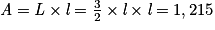 .
.
Donc : 1,5 × l2 = 1,215, soit en divisant par 1,5 : l2 = 0,81.
En prenant la racine carrée, on obtient :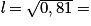 0,9 m.
0,9 m.
Et ensuite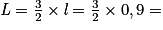 1,35 m.
1,35 m.
Donc la longueur du rectangle ABCD est de 1,35 m et sa largeur est de 0,9 m.
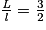 , alors
, alors 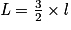 .
.Avec l'aire du rectangle ABCD, on obtient :
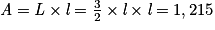 .
.Donc : 1,5 × l2 = 1,215, soit en divisant par 1,5 : l2 = 0,81.
En prenant la racine carrée, on obtient :
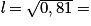 0,9 m.
0,9 m.Et ensuite
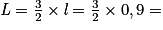 1,35 m.
1,35 m.Donc la longueur du rectangle ABCD est de 1,35 m et sa largeur est de 0,9 m.

