Énoncé
19 points
Dans cet exercice, on donnera, si nécessaire, une valeur approchée des résultats au centième près.
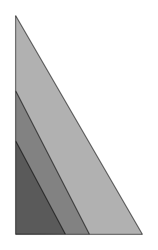
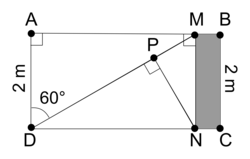
Pour construire le décor d'une pièce de théâtre (figure 1), Joanna dispose d'une plaque rectangulaire ABCD de 4 m sur 2 m dans laquelle elle doit découper les trois triangles du décor avant de les superposer. Elle propose un découpage de la plaque (figure 2).
Pour construire le décor d'une pièce de théâtre (figure 1), Joanna dispose d'une plaque rectangulaire ABCD de 4 m sur 2 m dans laquelle elle doit découper les trois triangles du décor avant de les superposer. Elle propose un découpage de la plaque (figure 2).
 |
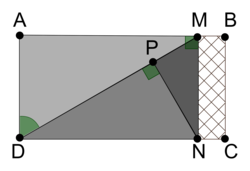 |
Pour cet exercice de géométrie, il est fortement conseillé de noter toutes les mesures données dans l'énoncé sur le schéma du découpage de la figure 2.
Il faut être vigilant et donner tous vos résultats en valeurs approchées au centième, car c'est précisé au début de l'exercice, et il ne faut pas l'oublier.
Il faut être vigilant et donner tous vos résultats en valeurs approchées au centième, car c'est précisé au début de l'exercice, et il ne faut pas l'oublier.
Le triangle ADM respecte les conditions suivantes :
• le triangle ADM est rectangle en A ;
• AD = 2 m ;
• 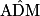 = 60°.
= 60°.
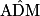 = 60°.
= 60°.1.
Montrer que [AM] mesure environ 3,46 m.
Comme ADM est un triangle rectangle, pour calculer la longueur d'un côté, il faut utiliser le théorème de Pythagore ou les formules de trigonométrie. Ici, vous ne pouvez pas utiliser le théorème de Pythagore, car on ne connaît qu'un côté du triangle.
Vous devez connaître les trois formules de trigonométrie (SOH CAH TOA) et savoir choisir la bonne formule en fonction du côté connu et du côté cherché dans le triangle.
Vous devez connaître les trois formules de trigonométrie (SOH CAH TOA) et savoir choisir la bonne formule en fonction du côté connu et du côté cherché dans le triangle.
2.
La partie de la plaque non utilisée est représentée en quadrillé sur la figure 2. Calculer une valeur approchée au centième de la proportion de la plaque qui n'est pas utilisée.
La plaque non utilisée correspond à une surface donc vous devez faire des calculs de proportion sur des aires.
3.
Pour que la superposition des triangles soit harmonieuse, Joanna veut que les trois triangles AMD, PNM et PDN soient semblables. Démontrer que c'est bien le cas.
Des triangles sont superposables si les triangles sont proportionnels, c'est-à-dire si leurs côtés sont proportionnels ou si leurs angles sont égaux. Les mesures d'angles sont souvent plus faciles à calculer, car les rédactions sont plus simples.
4.
Joanna aimerait que le coefficient d'agrandissement pour passer du triangle PDN au triangle AMD soit plus petit que 1,5. Est-ce le cas ? Justifier.
Pour calculer le coefficient d'agrandissement, vous devez connaître la mesure de deux côtés associés, un dans chacun des deux triangles. Comme ce sont des triangles rectangles, vous pouvez toujours utiliser la trigonométrie ou le théorème de Pythagore.
Corrigé
1.
 |
On sait que : ADM est un triangle rectangle en A ; 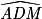 = 60° et AD = 2 m.
= 60° et AD = 2 m.
D'après :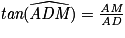
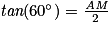 .
.
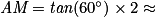 3,46 m.
3,46 m.
Donc [AM] mesure bien environ 3,46 m.
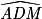 = 60° et AD = 2 m.
= 60° et AD = 2 m.D'après :
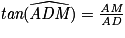
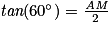 .
.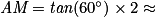 3,46 m.
3,46 m.Donc [AM] mesure bien environ 3,46 m.
2. La plaque ABCD a une forme de rectangle, son aire est : A = L × l = 4 × 2 = 8 m2.
La partie non utilisée de la plaque est le rectangle MBCN.
Comme [AM] mesure environ 3,46 m, et que [AB] mesure 4 m, cela signifie que [MB] mesure environ 0,54 m.
L'aire de la partie non utilisée est donc : A = L × l = 0,54 × 2 = 1,08 m2.
La proportion de la partie non utilisée est donc :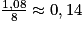 .
.
La partie non utilisée de la plaque est le rectangle MBCN.
Comme [AM] mesure environ 3,46 m, et que [AB] mesure 4 m, cela signifie que [MB] mesure environ 0,54 m.
L'aire de la partie non utilisée est donc : A = L × l = 0,54 × 2 = 1,08 m2.
La proportion de la partie non utilisée est donc :
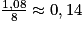 .
.3. Deux triangles sont semblables s'ils ont des côtés proportionnels ou si leurs angles sont de mêmes mesures.
Dans le triangle ADM :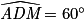 ;
; 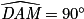 et donc
et donc 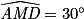 car la somme des angles d'un triangle vaut 180°.
car la somme des angles d'un triangle vaut 180°.
Dans le triangle PDN :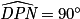 ;
; 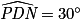 (car
(car 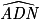 est un angle droit et
est un angle droit et 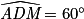 ) et
) et 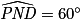 car la somme des angles d'un triangle vaut 180°.
car la somme des angles d'un triangle vaut 180°.
Dans le triangle PMN :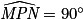 ;
; 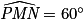 (car
(car 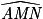 est un angle droit et
est un angle droit et 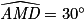 ) et
) et 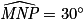 car la somme des angles d'un triangle vaut 180°.
car la somme des angles d'un triangle vaut 180°.
Donc les trois triangles ont trois angles de mêmes mesures, donc ils sont semblables.
Dans le triangle ADM :
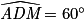 ;
; 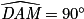 et donc
et donc 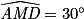 car la somme des angles d'un triangle vaut 180°.
car la somme des angles d'un triangle vaut 180°.Dans le triangle PDN :
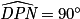 ;
; 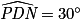 (car
(car 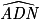 est un angle droit et
est un angle droit et 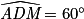 ) et
) et 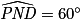 car la somme des angles d'un triangle vaut 180°.
car la somme des angles d'un triangle vaut 180°.Dans le triangle PMN :
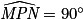 ;
; 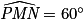 (car
(car 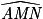 est un angle droit et
est un angle droit et 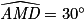 ) et
) et 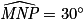 car la somme des angles d'un triangle vaut 180°.
car la somme des angles d'un triangle vaut 180°.Donc les trois triangles ont trois angles de mêmes mesures, donc ils sont semblables.
4. Comme les triangles PND et AMD sont semblables, on a donc les côtés [DM] et [DN] qui sont associés. (On a également les côtés [AM] et [DP] qui sont associés et les côtés [AD] et [PN] qui sont associés.)
Pour calculer le coefficient d'agrandissement, on calcule la longueur DM en utilisant le théorème de Pythagore (on peut aussi calculer la longueur DP ou la longueur PN avec les formules de trigonométrie).
On sait que : ADM est un triangle rectangle en A ; AM = 3,46 m ; AD = 2 m.
D'après le théorème de Pythagore :
DM2 = AM2 + AD2
DM2 = 3,462 + 22
DM2 = 11,9716 + 4
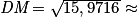 4 m.
4 m.
Pour calculer le coefficient d'agrandissement, on fait :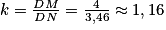 .
.
Le coefficient d'agrandissement pour passer du triangle PDN au triangle AMD est donc de 1,16 donc il est plus petit que 1,5.
Pour calculer le coefficient d'agrandissement, on calcule la longueur DM en utilisant le théorème de Pythagore (on peut aussi calculer la longueur DP ou la longueur PN avec les formules de trigonométrie).
On sait que : ADM est un triangle rectangle en A ; AM = 3,46 m ; AD = 2 m.
D'après le théorème de Pythagore :
DM2 = AM2 + AD2
DM2 = 3,462 + 22
DM2 = 11,9716 + 4
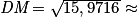 4 m.
4 m.Pour calculer le coefficient d'agrandissement, on fait :
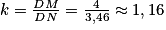 .
.Le coefficient d'agrandissement pour passer du triangle PDN au triangle AMD est donc de 1,16 donc il est plus petit que 1,5.

