Sujet de métropole, juin 2018, exercice 7
Énoncé
17 points
Le hand-spinner est une sorte de toupie plate qui tourne sur elle-même.
 |
On donne au hand-spinner une vitesse de rotation initiale au temps t = 0, puis, au cours du temps, sa vitesse de rotation diminue jusqu'à l'arrêt complet du hand-spinner. Sa vitesse de rotation est alors égale à 0.
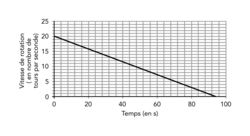
Grâce à un appareil de mesure, on a relevé la vitesse de rotation exprimée en nombre de tours par seconde.
Sur le graphique ci-dessous, on a représenté cette vitesse en fonction du temps exprimé en seconde :
Grâce à un appareil de mesure, on a relevé la vitesse de rotation exprimée en nombre de tours par seconde.
Sur le graphique ci-dessous, on a représenté cette vitesse en fonction du temps exprimé en seconde :
 |
1.
Le temps et la vitesse de rotation du hand-spinner sont-ils proportionnels ? Justifier.
Rappelez-vous du lien qui existe entre situation de proportionnalité et représentation graphique.
2.
Par lecture graphique, répondre aux questions suivantes :
a)
Quelle est la vitesse de rotation initiale du hand-spinner (en nombre de tours par seconde) ?
Remarquez qu'il s'agit de déterminer l'ordonnée y du point de la droite qui a pour abscisse t = 0.
b)
Quelle est la vitesse de rotation du hand-spinner (en nombre de tours par seconde) au bout de 1 minute et 20 secondes ?
Remarquez que 1 min 20 s= 80 s.
c)
Au bout de combien de temps, le hand-spinner va-t-il s'arrêter ?
Remarquez qu'il s'agit de déterminer l'abscisse t du point de la droite qui a pour ordonnée y = 0.
3.
Pour calculer la vitesse de rotation du hand-spinner en fonction du temps t, notée V(t), on utilise la fonction suivante :
V(t) = −0,214 × t + Vinitiale
V(t) = −0,214 × t + Vinitiale
- t est le temps (exprimé en seconde) qui s'est écoulé depuis le début de la rotation du hand-spinner.
- Vinitiale est la vitesse de rotation à laquelle on a lancé le hand-spinner au départ.
a)
On lance le hand-spinner à une vitesse initiale de 20 tours par seconde. Sa vitesse de rotation est donc donnée par la formule : V(t) = −0,214 × t + 20. Calculer sa vitesse de rotation au bout de 30 s.
Il s'agit de calculer V(30).
b)
Au bout de combien de temps le hand-spinner va-t-il s'arrêter ? Justifier par un calcul.
Remarquez qu'il s'agit de déterminer, par le calcul, le temps t tel que V(t) = 0.
c)
Est-il vrai que, d'une manière générale, si l'on fait tourner le hand-spinner deux fois plus vite au départ, il tournera deux fois plus longtemps ? Justifier.
Modifiez l'expression V(t) et résolvez la nouvelle équation V(t) = 0.
Annexes
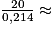93,5 s au dixième près.
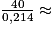186,9 s au dixième près.
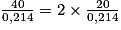. © 2000-2024, rue des écoles