Sujet de métropole, juin 2017, exercice 6
Énoncé
8 points
Document 1
Le surpoids est devenu un problème majeur de santé, celui-ci prédispose à beaucoup de maladies et diminue l'espérance de vie.
L'indice le plus couramment utilisé est celui de masse corporelle (IMC).
Le surpoids est devenu un problème majeur de santé, celui-ci prédispose à beaucoup de maladies et diminue l'espérance de vie.
L'indice le plus couramment utilisé est celui de masse corporelle (IMC).
Document 2
L'IMC est une grandeur internationale permettant de déterminer la corpulence d'une personne adulte entre 18 ans et 65 ans.
Il se calcule avec la formule suivante :
IMC =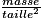
avec « masse » en kg et « taille » en m.
Normes :
L'IMC est une grandeur internationale permettant de déterminer la corpulence d'une personne adulte entre 18 ans et 65 ans.
Il se calcule avec la formule suivante :
IMC =
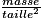
avec « masse » en kg et « taille » en m.
Normes :
- 18,5
 IMC < 25 : corpulence normale ;
IMC < 25 : corpulence normale ; - 25
 IMC < 30 : surpoids ;
IMC < 30 : surpoids ; - IMC
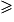 30 : obésité.
30 : obésité.
1.
Dans une entreprise, lors d'une visite médicale, un médecin calcule l'IMC de six des employés. Il utilise pour cela une feuille de tableur dont voici un extrait :
 |
a)
Combien d'employés sont en situation de surpoids ou d'obésité dans cette entreprise ?
Rappelez-vous qu'une personne est en situation de surpoids ou d'obésité lorsque son IMC est supérieur ou égal à 25.
b)
Laquelle de ces formules a-t-on écrite dans la cellule B3, puis recopiée à droite, pour calculer l'IMC ?
Recopier la formule correcte sur la copie.
Recopier la formule correcte sur la copie.
 |
Observez la formule de l'IMC et les cases où sont situées les masses et les tailles.
2.
Le médecin a fait le bilan de l'IMC de chacun des 41 employés de cette entreprise. Il a reporté les informations recueillies dans le tableau suivant dans lequel les IMC ont été arrondis à l'unité près.
| IMC | 20 | 22 | 23 | 24 | 25 | 29 | 30 | 33 | Total |
| Effectif | 9 | 12 | 6 | 8 | 2 | 1 | 1 | 2 | 41 |
a)
Calculer une valeur approchée, arrondie à l'entier près, de l'IMC moyen des employés de cette entreprise.
N'oubliez pas de pondérer chaque valeur de l'IMC par son effectif.
b)
Quel est l'IMC médian ? Interpréter ce résultat.
Rappelle-toi que la médiane d'une série statistique est une valeur qui partage cette série en deux groupes d'effectifs égaux : 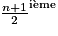 des valeurs classées par ordre croissant.
des valeurs classées par ordre croissant.
- un groupe constitué de valeurs inférieures ou égales à la médiane ;
- un groupe constitué de valeurs supérieures ou égales à la médiane.
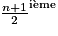 des valeurs classées par ordre croissant.
des valeurs classées par ordre croissant.c)
On lit sur certains magazines : « On estime qu'au moins 5 % de la population mondiale est en surpoids ou est obèse. » Est-ce le cas pour les employés de cette entreprise ?
Rappelez-vous qu'une personne est en situation de surpoids ou d'obésité lorsque son IMC est supérieur ou égal à 25.
Annexes
© 2000-2025, Miscellane
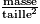 .
.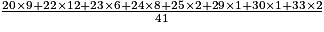
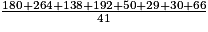
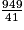
 23 à l'entier près.
23 à l'entier près.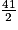 = 20,5 donc la médiane de cette série statistique est la 21e des valeurs classées par ordre croissant.
= 20,5 donc la médiane de cette série statistique est la 21e des valeurs classées par ordre croissant.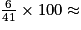 14,6 % au dixième près.
14,6 % au dixième près.