Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2017, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2017, exercice 1
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2017, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2017, exercice 1
Énoncé
4 points
Dans une urne contenant des boules vertes et des boules bleues, on tire au hasard une boule et on regarde sa couleur. On replace ensuite la boule dans l'urne et on mélange les boules.
La probabilité d'obtenir une boule verte est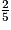 .
.
La probabilité d'obtenir une boule verte est
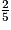 .
.1.
Expliquer pourquoi la probabilité d'obtenir une boule bleue est égale à 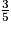 .
.
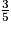 .
.Pensez à l'événement contraire.
2.
Paul a effectué 6 tirages et a obtenu une boule verte à chaque fois.
Au 7e tirage, aura-t-il plus de chances d'obtenir une boule bleue qu'une boule verte ?
Au 7e tirage, aura-t-il plus de chances d'obtenir une boule bleue qu'une boule verte ?
Rappelez-vous qu'après chaque tirage, la boule est remise dans l'urne.
3.
Déterminer le nombre de boules bleues dans cette urne sachant qu'il y a 8 boules vertes.
Notez x le nombre de boules bleues, mettez en équation le problème et résolvez cette équation.
Vous pouvez aussi utiliser la proportionnalité et les valeurs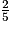 ,
, 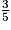 et 8.
et 8.
Vous pouvez aussi utiliser la proportionnalité et les valeurs
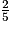 ,
, 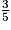 et 8.
et 8.Corrigé
1. L'urne contient des boules vertes et des boules bleues. L'événement « obtenir une boule bleue » est donc l'événement contraire de l'événement « obtenir une boule verte ».
La probabilité d'obtenir une boule bleue est donc égale à 1 −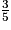 =
= 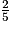 .
.
La probabilité d'obtenir une boule bleue est donc égale à 1 −
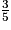 =
= 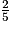 .
.2. D'après l'énoncé, la boule est remise dans l'urne après chaque tirage.
Au 7e tirage, la probabilité d'obtenir une boule verte sera toujours de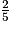 et celle d'obtenir une boule bleue de
et celle d'obtenir une boule bleue de 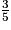 .
.
Paul aura donc plus de chances d'obtenir une boule bleue qu'une boule verte.
Au 7e tirage, la probabilité d'obtenir une boule verte sera toujours de
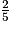 et celle d'obtenir une boule bleue de
et celle d'obtenir une boule bleue de 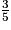 .
.Paul aura donc plus de chances d'obtenir une boule bleue qu'une boule verte.
3. Notons x le nombre de boules bleues.
L'urne contient x boules bleues parmi x + 8 boules, donc la probabilité d'obtenir une boule bleue est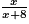 .
.
Sachant que la probabilité d'obtenir une boule bleue est de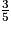 , on a :
, on a :
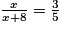 ;
;
soit 5 × x = 3 × (x + 8) en utilisant l'égalité des produits en croix ;
et 5x = 3x + 3 × 8 en développant l'expression ;
5x − 3x = 24 ;
2x = 24 ;
x =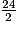 ;
;
x = 12.
Sachant qu'il y a 8 boules vertes dans cette urne, il y a 12 boules bleues.
Remarque : plus rapidement, en utilisant la proportionnalité,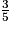 = 1,5 ×
= 1,5 × 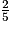 donc il y a 1,5 × 8 = 12 boules bleues dans cette urne.
donc il y a 1,5 × 8 = 12 boules bleues dans cette urne.
L'urne contient x boules bleues parmi x + 8 boules, donc la probabilité d'obtenir une boule bleue est
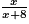 .
.Sachant que la probabilité d'obtenir une boule bleue est de
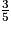 , on a :
, on a :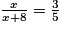 ;
;soit 5 × x = 3 × (x + 8) en utilisant l'égalité des produits en croix ;
et 5x = 3x + 3 × 8 en développant l'expression ;
5x − 3x = 24 ;
2x = 24 ;
x =
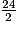 ;
;x = 12.
Sachant qu'il y a 8 boules vertes dans cette urne, il y a 12 boules bleues.
Remarque : plus rapidement, en utilisant la proportionnalité,
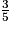 = 1,5 ×
= 1,5 × 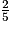 donc il y a 1,5 × 8 = 12 boules bleues dans cette urne.
donc il y a 1,5 × 8 = 12 boules bleues dans cette urne.Corrigé
1. L'urne contient des boules vertes et des boules bleues. L'événement « obtenir une boule bleue » est donc l'événement contraire de l'événement « obtenir une boule verte ».
La probabilité d'obtenir une boule bleue est donc égale à 1 −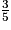 =
= 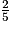 .
.
La probabilité d'obtenir une boule bleue est donc égale à 1 −
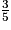 =
= 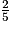 .
.2. D'après l'énoncé, la boule est remise dans l'urne après chaque tirage.
Au 7e tirage, la probabilité d'obtenir une boule verte sera toujours de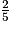 et celle d'obtenir une boule bleue de
et celle d'obtenir une boule bleue de 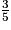 .
.
Paul aura donc plus de chances d'obtenir une boule bleue qu'une boule verte.
Au 7e tirage, la probabilité d'obtenir une boule verte sera toujours de
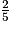 et celle d'obtenir une boule bleue de
et celle d'obtenir une boule bleue de 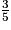 .
.Paul aura donc plus de chances d'obtenir une boule bleue qu'une boule verte.
3. Notons x le nombre de boules bleues.
L'urne contient x boules bleues parmi x + 8 boules, donc la probabilité d'obtenir une boule bleue est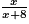 .
.
Sachant que la probabilité d'obtenir une boule bleue est de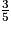 , on a :
, on a :
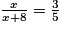 ;
;
soit 5 × x = 3 × (x + 8) en utilisant l'égalité des produits en croix ;
et 5x = 3x + 3 × 8 en développant l'expression ;
5x − 3x = 24 ;
2x = 24 ;
x =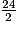 ;
;
x = 12.
Sachant qu'il y a 8 boules vertes dans cette urne, il y a 12 boules bleues.
Remarque : plus rapidement, en utilisant la proportionnalité,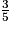 = 1,5 ×
= 1,5 × 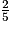 donc il y a 1,5 × 8 = 12 boules bleues dans cette urne.
donc il y a 1,5 × 8 = 12 boules bleues dans cette urne.
L'urne contient x boules bleues parmi x + 8 boules, donc la probabilité d'obtenir une boule bleue est
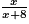 .
.Sachant que la probabilité d'obtenir une boule bleue est de
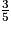 , on a :
, on a :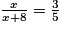 ;
;soit 5 × x = 3 × (x + 8) en utilisant l'égalité des produits en croix ;
et 5x = 3x + 3 × 8 en développant l'expression ;
5x − 3x = 24 ;
2x = 24 ;
x =
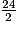 ;
;x = 12.
Sachant qu'il y a 8 boules vertes dans cette urne, il y a 12 boules bleues.
Remarque : plus rapidement, en utilisant la proportionnalité,
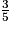 = 1,5 ×
= 1,5 × 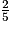 donc il y a 1,5 × 8 = 12 boules bleues dans cette urne.
donc il y a 1,5 × 8 = 12 boules bleues dans cette urne.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2017, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2017, exercice 1
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2017, exercice 1
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2017, exercice 1

