Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet zéro du ministère, 2017, exercice 5
Mathématiques - Travailler sur des sujets de brevet
Sujet zéro du ministère, 2017, exercice 5
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet zéro du ministère, 2017, exercice 5
Mathématiques - Travailler sur des sujets de brevet
Sujet zéro du ministère, 2017, exercice 5
Énoncé
Pour régler les feux de croisement d'une automobile, on la place face à un mur vertical. Le phare, identifié au point P, émet un faisceau lumineux dirigé vers le sol.
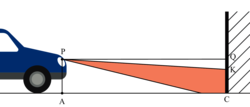 |
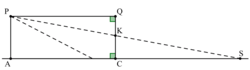
On relève les mesures suivantes : PA = 0,7 m, AC = QP = 5 m et CK = 0,61 m.
Sur le schéma ci-dessous, qui n'est pas à l'échelle, le point S représente l'endroit où le rayon supérieur du faisceau rencontrerait le sol en l'absence du mur.
 |
On considère que les feux de croisement sont bien réglés si le rapport 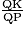 est compris entre 0,015 et 0,02.
est compris entre 0,015 et 0,02.
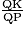 est compris entre 0,015 et 0,02.
est compris entre 0,015 et 0,02.1.
Vérifier que les feux de croisement de la voiture sont bien réglés.
Remarquez que QK = QC − CK.
2.
À quelle distance maximale de la voiture un obstacle se trouvant sur la route est-il éclairé par les feux de croisement ?
Remarquez qu'il s'agit de calculer la longueur AS et pensez à utiliser le théorème de Thalès ou la trigonométrie.
Corrigé
1.
D'après les illustrations, on a : QK = QC − CK = PA − CK = 0,7 − 0,61 = 0,09.
On a donc :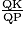 =
= 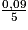 = 0,18.
= 0,18.
On a donc :
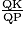 =
= 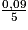 = 0,18.
= 0,18. Les feux de croisement de la voiture sont réglés avec une inclinaison de 0,018.
0,015 < 0,018 < 0,02 donc ils sont bien réglés.
0,015 < 0,018 < 0,02 donc ils sont bien réglés.
2.  =
= 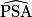 donc tan (
donc tan (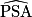 ) = tan (
) = tan ( ), puis
), puis 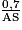 = 0,018 et AS =
= 0,018 et AS = 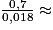 38,89 m au centimètre près.
38,89 m au centimètre près.
La distance maximale de la voiture qu'éclairent les feux de croisement sur la route est la longueur AS.
Calculons-la par trois méthodes différentes.
Calculons-la par trois méthodes différentes.
Méthode 1 : à l'aide de l'angle 

Les droites (PQ) et (AS) sont parallèles.
Les angles =
=  et
et 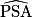 sont donc alternes internes et égaux.
sont donc alternes internes et égaux.
Les angles
 =
=  et
et 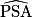 sont donc alternes internes et égaux.
sont donc alternes internes et égaux.Dans le triangle PAS rectangle en A, on a :
tan (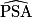 ) =
) = 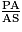 =
= 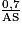 .
.
tan (
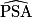 ) =
) = 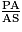 =
= 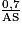 .
.Dans le triangle PQK rectangle en Q, on a :
tan ( ) =
) = 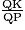 = 0,018 d'après la question 1.
= 0,018 d'après la question 1.
tan (
 ) =
) = 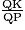 = 0,018 d'après la question 1.
= 0,018 d'après la question 1. =
= 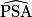 donc tan (
donc tan (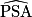 ) = tan (
) = tan ( ), puis
), puis 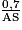 = 0,018 et AS =
= 0,018 et AS = 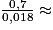 38,89 m au centimètre près.
38,89 m au centimètre près.Méthode 2 : à l'aide du théorème de Thalès (configuration n° 1)
Dans le triangle PAS, K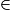 [PS], C
[PS], C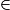 [AS] et les droites (KC) et (PA) sont parallèles, donc d'après le théorème de Thalès :
[AS] et les droites (KC) et (PA) sont parallèles, donc d'après le théorème de Thalès :
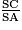 =
= 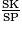 =
= 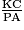 , donc en particulier
, donc en particulier 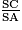 =
= 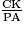 .
.
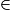 [PS], C
[PS], C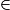 [AS] et les droites (KC) et (PA) sont parallèles, donc d'après le théorème de Thalès :
[AS] et les droites (KC) et (PA) sont parallèles, donc d'après le théorème de Thalès :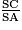 =
= 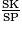 =
= 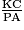 , donc en particulier
, donc en particulier 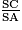 =
= 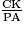 .
.CK = 0,61, PA = 0,7 et, en notant SC = x, on a AS = x + 5.
On a donc :
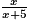 =
= 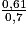
0,7x = 0,61(x + 5)
0,7x − 0,61x = 0,61 × 5 = 3,05
0,09x = 3,05
x =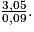
AS = x + 5 =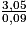 + 5
+ 5  38,89 m au centimètre près.
38,89 m au centimètre près.
On a donc :
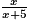 =
= 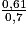
0,7x = 0,61(x + 5)
0,7x − 0,61x = 0,61 × 5 = 3,05
0,09x = 3,05
x =
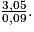
AS = x + 5 =
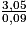 + 5
+ 5  38,89 m au centimètre près.
38,89 m au centimètre près.Méthode 3 : à l'aide du théorème de Thalès (configuration n° 2 dite « en papillon »)
K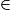 [PS], K
[PS], K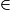 [QC] et les droites (PQ) et (CS) sont parallèles, donc d'après le théorème de Thalès :
[QC] et les droites (PQ) et (CS) sont parallèles, donc d'après le théorème de Thalès :
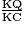 =
= 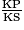 =
= 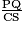 , donc en particulier
, donc en particulier 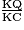 =
= 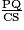 .
.
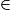 [PS], K
[PS], K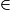 [QC] et les droites (PQ) et (CS) sont parallèles, donc d'après le théorème de Thalès :
[QC] et les droites (PQ) et (CS) sont parallèles, donc d'après le théorème de Thalès :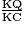 =
= 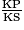 =
= 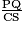 , donc en particulier
, donc en particulier 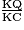 =
= 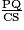 .
.KQ = 0,09, KC = 0,61, PQ = 5, donc :
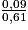 =
= 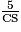 ;
;
CS =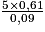 =
= 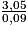 puis :
puis :
AS = AC + CS =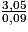 + 5
+ 5  38,89 m au centimètre près.
38,89 m au centimètre près.
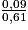 =
= 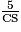 ;
;CS =
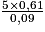 =
= 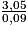 puis :
puis :AS = AC + CS =
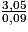 + 5
+ 5  38,89 m au centimètre près.
38,89 m au centimètre près.Corrigé
1.
D'après les illustrations, on a : QK = QC − CK = PA − CK = 0,7 − 0,61 = 0,09.
On a donc :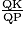 =
= 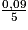 = 0,18.
= 0,18.
On a donc :
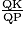 =
= 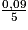 = 0,18.
= 0,18. Les feux de croisement de la voiture sont réglés avec une inclinaison de 0,018.
0,015 < 0,018 < 0,02 donc ils sont bien réglés.
0,015 < 0,018 < 0,02 donc ils sont bien réglés.
2.  =
= 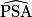 donc tan (
donc tan (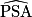 ) = tan (
) = tan ( ), puis
), puis 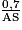 = 0,018 et AS =
= 0,018 et AS = 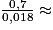 38,89 m au centimètre près.
38,89 m au centimètre près.
La distance maximale de la voiture qu'éclairent les feux de croisement sur la route est la longueur AS.
Calculons-la par trois méthodes différentes.
Calculons-la par trois méthodes différentes.
Méthode 1 : à l'aide de l'angle 

Les droites (PQ) et (AS) sont parallèles.
Les angles =
=  et
et 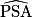 sont donc alternes internes et égaux.
sont donc alternes internes et égaux.
Les angles
 =
=  et
et 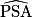 sont donc alternes internes et égaux.
sont donc alternes internes et égaux.Dans le triangle PAS rectangle en A, on a :
tan (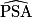 ) =
) = 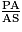 =
= 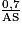 .
.
tan (
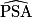 ) =
) = 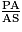 =
= 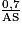 .
.Dans le triangle PQK rectangle en Q, on a :
tan ( ) =
) = 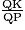 = 0,018 d'après la question 1.
= 0,018 d'après la question 1.
tan (
 ) =
) = 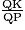 = 0,018 d'après la question 1.
= 0,018 d'après la question 1. =
= 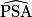 donc tan (
donc tan (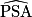 ) = tan (
) = tan ( ), puis
), puis 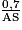 = 0,018 et AS =
= 0,018 et AS = 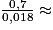 38,89 m au centimètre près.
38,89 m au centimètre près.Méthode 2 : à l'aide du théorème de Thalès (configuration n° 1)
Dans le triangle PAS, K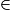 [PS], C
[PS], C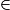 [AS] et les droites (KC) et (PA) sont parallèles, donc d'après le théorème de Thalès :
[AS] et les droites (KC) et (PA) sont parallèles, donc d'après le théorème de Thalès :
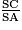 =
= 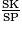 =
= 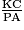 , donc en particulier
, donc en particulier 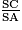 =
= 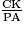 .
.
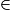 [PS], C
[PS], C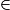 [AS] et les droites (KC) et (PA) sont parallèles, donc d'après le théorème de Thalès :
[AS] et les droites (KC) et (PA) sont parallèles, donc d'après le théorème de Thalès :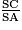 =
= 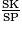 =
= 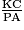 , donc en particulier
, donc en particulier 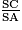 =
= 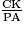 .
.CK = 0,61, PA = 0,7 et, en notant SC = x, on a AS = x + 5.
On a donc :
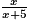 =
= 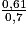
0,7x = 0,61(x + 5)
0,7x − 0,61x = 0,61 × 5 = 3,05
0,09x = 3,05
x =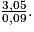
AS = x + 5 =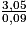 + 5
+ 5  38,89 m au centimètre près.
38,89 m au centimètre près.
On a donc :
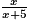 =
= 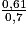
0,7x = 0,61(x + 5)
0,7x − 0,61x = 0,61 × 5 = 3,05
0,09x = 3,05
x =
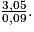
AS = x + 5 =
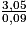 + 5
+ 5  38,89 m au centimètre près.
38,89 m au centimètre près.Méthode 3 : à l'aide du théorème de Thalès (configuration n° 2 dite « en papillon »)
K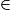 [PS], K
[PS], K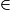 [QC] et les droites (PQ) et (CS) sont parallèles, donc d'après le théorème de Thalès :
[QC] et les droites (PQ) et (CS) sont parallèles, donc d'après le théorème de Thalès :
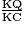 =
= 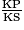 =
= 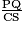 , donc en particulier
, donc en particulier 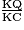 =
= 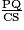 .
.
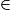 [PS], K
[PS], K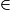 [QC] et les droites (PQ) et (CS) sont parallèles, donc d'après le théorème de Thalès :
[QC] et les droites (PQ) et (CS) sont parallèles, donc d'après le théorème de Thalès :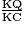 =
= 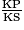 =
= 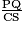 , donc en particulier
, donc en particulier 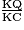 =
= 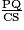 .
.KQ = 0,09, KC = 0,61, PQ = 5, donc :
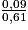 =
= 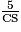 ;
;
CS =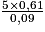 =
= 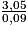 puis :
puis :
AS = AC + CS =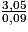 + 5
+ 5  38,89 m au centimètre près.
38,89 m au centimètre près.
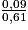 =
= 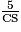 ;
;CS =
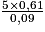 =
= 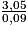 puis :
puis :AS = AC + CS =
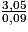 + 5
+ 5  38,89 m au centimètre près.
38,89 m au centimètre près.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet zéro du ministère, 2017, exercice 5
Mathématiques - Travailler sur des sujets de brevet
Sujet zéro du ministère, 2017, exercice 5
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet zéro du ministère, 2017, exercice 5
Mathématiques - Travailler sur des sujets de brevet
Sujet zéro du ministère, 2017, exercice 5

