Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2014, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2014, exercice 4
Énoncé
3 points
Un sac contient 20 jetons qui sont soit jaunes, soit verts, soit rouges, soit bleus. On considère l'expérience suivante : tirer au hasard un jeton, noter sa couleur et remettre le jeton dans le sac. Chaque jeton a la même probabilité d'être tiré.
1.
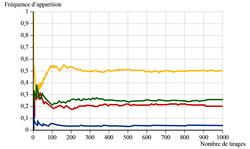
Le professeur, qui connaît la composition du sac, a simulé un grand nombre de fois l'expérience avec un tableur. Il a représenté ci-dessous la fréquence d'apparition des différentes couleurs en fonction du nombre de tirages.
 |
a)
Quelle couleur est la plus présente dans le sac ? Aucune justification n'est attendue.
Pour répondre, observez le graphique.
b)
Le professeur a construit la feuille de calcul ci-après. Quelle formule a-t-il saisie dans la cellule C2 avant de la recopier vers le bas ?
| | A | B | C |
|---|---|---|---|
| 1 | Nombre de tirages | Nombre de fois où un jeton rouge est apparu | Fréquence d'apparition de la couleur rouge |
| 2 | 1 | 0 | 0 |
| 3 | 2 | 0 | 0 |
| 4 | 3 | 0 | 0 |
| 5 | 4 | 0 | 0 |
| 6 | 5 | 0 | 0 |
| 7 | 6 | 1 | 0,166666667 |
| 8 | 7 | 1 | 0,142857143 |
| 9 | 8 | 1 | 0,125 |
| 10 | 9 | 1 | 0,111111111 |
| 11 | 10 | 1 | 0,1 |
La formule de la fréquence est f = 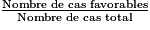 .
.
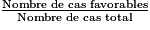 .
.2.
On sait que la probabilité de tirer un jeton rouge est de 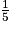 .
.
Combien y a-t-il de jetons rouges dans ce sac ?
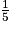 .
.Combien y a-t-il de jetons rouges dans ce sac ?
La probabilité de tirer un jeton rouge est P = 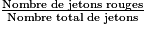 .
.
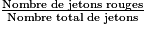 .
.Corrigé
1.
a) La couleur la plus présente dans le sac est le jaune, car c'est la couleur pour laquelle la fréquence d'apparition est la plus élevée.
b) Le nombre de la cellule C2 est le quotient du nombre de la cellule B2 par celui de la cellule A2.
Dans la cellule C2, on a donc saisi la formule « = B2/A2 » et on l'a recopié vers le bas.
Dans la cellule C2, on a donc saisi la formule « = B2/A2 » et on l'a recopié vers le bas.
2.
En notant n le nombre de jetons rouges dans ce sac, on a :
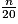 =
= 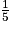 donc 5n = 20, puis n =
donc 5n = 20, puis n = 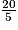 = 4.
= 4.
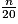 =
= 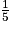 donc 5n = 20, puis n =
donc 5n = 20, puis n = 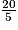 = 4.
= 4.Dans ce sac, si la probabilité de tirer un jeton rouge est de 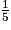 , il y a 4 jetons rouges.
, il y a 4 jetons rouges.
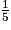 , il y a 4 jetons rouges.
, il y a 4 jetons rouges.Corrigé
1.
a) La couleur la plus présente dans le sac est le jaune, car c'est la couleur pour laquelle la fréquence d'apparition est la plus élevée.
b) Le nombre de la cellule C2 est le quotient du nombre de la cellule B2 par celui de la cellule A2.
Dans la cellule C2, on a donc saisi la formule « = B2/A2 » et on l'a recopié vers le bas.
Dans la cellule C2, on a donc saisi la formule « = B2/A2 » et on l'a recopié vers le bas.
2.
En notant n le nombre de jetons rouges dans ce sac, on a :
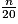 =
= 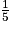 donc 5n = 20, puis n =
donc 5n = 20, puis n = 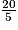 = 4.
= 4.
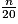 =
= 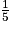 donc 5n = 20, puis n =
donc 5n = 20, puis n = 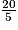 = 4.
= 4.Dans ce sac, si la probabilité de tirer un jeton rouge est de 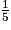 , il y a 4 jetons rouges.
, il y a 4 jetons rouges.
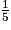 , il y a 4 jetons rouges.
, il y a 4 jetons rouges.
Signaler une erreur
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2014, exercice 4
Imprimer
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2014, exercice 4
Mathématiques - Travailler sur des sujets de brevet
Sujet de métropole, juin 2014, exercice 4

