Utiliser le cosinus d'un angle dans un triangle rectangle

Fiche

Cas d'un triangle AIU rectangle en A

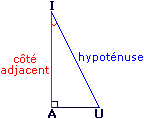Utiliser le cosinus d'un angle dans un triangle rectangle - illustration 1

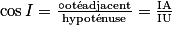
$\cos{I} = \frac{\mathrm{\circ{o}t\acute{e} adjacent}}{\mathrm{hypot\acute{e}nuse}}= \frac{\mathrm{IA}}{\mathrm{IU}}$
d'où IA = IU × cos Î ;
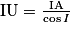
$\mathrm{IU} = \frac{\mathrm{IA}}{\cos{I}}$

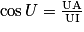
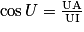
Dans AIU, on a aussi : $\cos{U} = \frac{\mathrm{UA}}{\mathrm{UI}}$

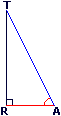
Cas d'un triangle RAT rectangle en R

Dans le triangle RAT, AR = 3 ; RT = 4 ; AT = 5.

Utiliser le cosinus d'un angle dans un triangle rectangle - illustration 2

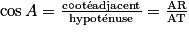
$\cos{A} = \frac{\mathrm{c\circ{o}t\acute{e} adjacent}}{\mathrm{hypot\acute{e}nuse}}= \frac{\mathrm{AR}}{\mathrm{AT}}$
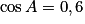
$\cos{A} = 0,6$
d'où 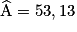$\widehat{\mathrm{A}} = 53,13°$ (valeur approchée).

Attention à bien repérer le côté adjacent à l'angle (celui qui est « à côté de » l'angle).