Il existe 4 façons de définir une fonction.
• Avec une phrase :
Soit f la fonction qui à un nombre associe son carré.
Soit f la fonction qui à un nombre associe son carré.
• Avec une formule :
f : x → x2 ou f(x) = x2
On dit alors que x2 est l'image de x par la fonction f.
f : x → x2 ou f(x) = x2
On dit alors que x2 est l'image de x par la fonction f.
• Avec un tableau :
| x | -3 | -2 | 0 | 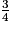 | 1 | 1,3 | 3 |
|---|---|---|---|---|---|---|---|
| f(x) | 9 | 4 | 0 | 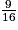 | 1 | 1,69 | 9 |
Pour calculer les valeurs de la seconde ligne, on élève au carré les nombres de la première ligne.
On a f(-3) = (-3)2 = 9, f(-2) = (-2)2 = 4, etc.
On dit que 9 est l'image de -3 par la fonction f.
-3 est un antécédent de 9 par la fonction f.
• Avec un graphique :
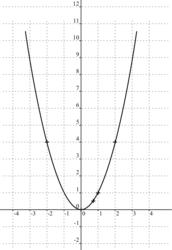
Pour tracer la fonction, on utilise un tableau de valeurs : les valeurs de x en abscisse et celles de f(x) en ordonnée pour chaque point.
Pour tracer la fonction, on utilise un tableau de valeurs : les valeurs de x en abscisse et celles de f(x) en ordonnée pour chaque point.
 |
Exercice n°1
Détermine la fonction qui correspond à la phrase suivante.
Écrivez la réponse dans la zone colorée.
La fonction qui à un nombre associe son double : x → .
Le double d'un nombre x est égal à 2 × x, que l'on écrit 2x.
Exercice n°2
Si x → 4x + 5, alors f(x) = 4x + 5.
Vrai ou faux ?
Vrai ou faux ?
Cochez la bonne réponse.
| ||
|
C'est la définition d'une fonction.
Exercice n°3
Si f(x) = 2x, alors x → 2x − 1.
Vrai ou faux ?
Vrai ou faux ?
Cochez la bonne réponse.
| ||
|
Exercice n°4
On considère la fonction g qui à un nombre associe son carré augmenté de 5.
1. Pour tout réel x, l'expression de g(x) est égale à :
Cochez la bonne réponse.
| ||
| ||
| ||
|
2. La représentation graphique de la fonction g est donnée :
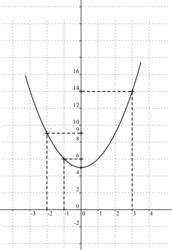 |
Complète les phrases suivantes par les termes l'image ou un antécédent. Pour cela, appuie-toi sur les résultats trouvés à la question 2.
Écrivez les réponses dans les zones colorées.
a. 14 est de 3.
b. 3 est de 14.
c. de 0 est 5.
d. de 6 est -1.
1. Le carré d'un nombre x est égal à x2.
Augmenter de 5 se traduit par + 5.
Donc g(x) = x2 + 5.
Augmenter de 5 se traduit par + 5.
Donc g(x) = x2 + 5.
3.
a. 14 est l'image de 3 car g(3) = 14.
b. 3 est un antécédent de 14 car g(3) = 14.
c. L'image de 0 est 5 car g(0) = 5.
d. Un antécédent de 6 est -1 car g(-1) = 6.

