Déterminer une fonction linéaire d'après un énoncé

Exemple 1

La puissance, P, d'un moteur électrique alimenté par une batterie de 12 V est proportionnelle à l'intensité, I, du courant.
Le coefficient de proportionnalité est égal à la tension.

• Les trois affirmations suivantes sont équivalentes :

la puissance est proportionnelle à l'intensité ;
le coefficient de proportionnalité est égal à la tension ;
P = 12 ×I.

• Cette formule définit une fonction linéaire : P(I) = 12 I.
Si I = 15 A, alors P(15) = 12 × 15 = 180.

Conclusion : la puissance d'un moteur qui utilise une intensité de 15 A est 180 W.

Exemple 2

Le périmètre d'un carré est proportionnel à la longueur de son côté.

• Si x désigne la mesure du côté du carré et si p désigne le périmètre du carré, alors la fonction linéaire associée à ce problème est : p(x) = 4 x.

• Ainsi un carré de 7,5 cm de côté a un périmètre de 30 cm car p(7,5) = 4 × 7,5.

Exercice n°1

Complète les réponses suivantes.

Écrivez les réponses dans les zones colorées.

1. Dans un supermarché, le kg de pommes coûte 1,25 €.
La fonction qui, à la masse m (en kg) de pommes, associe son prix (en €) est la fonction :
m → m.

2. Un commerçant décide d'augmenter tous ses prix de 18 %.
La fonction qui, à chaque prix p (en €), associe le montant (en €) de l'augmentation est la fonction :
p → p.

Exercice n°2

Complète la réponse suivante.

Écrivez les réponses dans les zones colorées.

Une automobile consomme 7,5 l de carburant pour 100 km parcourus à 90 km/h.
La fonction qui, au nombre x de litres de carburant contenus dans le réservoir, associe la distance (en km) que peut parcourir l'automobile à 90 km/h est la fonction :
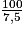→ $\frac{100}{7,5}$ .

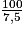Exercice n°3

Une voiture consomme 9 L aux 100 km.
Complète les phrases suivantes.

Écrivez les réponses dans les zones colorées.

a. Exprimer la consommation de la voiture en fonction du nombre de km, c'est définir une fonction linéaire f telle que : f(x) = x.

b. Par conséquent : f(125) = .
Pour faire km, la voiture a consommé litres d'essence.

a. 9 L pour 100 km correspond à 0,09 L par km.

b. Pour x km, la consommation est donc de x fois 0,09 L :
f(x) = 0,09x
f(125) = 0,09 × 125 = 11,25

Exercice n°4

Le livret d'épargne de Jean lui rapporte 4,5 % d'intérêts annuels.
Réponds aux questions.

Écrivez les réponses dans les zones colorées.

a. Jean a placé 50 €. Quels intérêts perçoit-il au bout d'un an ? €.

b. Exprimer le montant des intérêts au bout d'un an en fonction du capital x, c'est définir une fonction linéaire f telle que : f(x) = x.

c. Pauline a placé de l'argent au même taux et a perçu 3,15 € d'intérêt. Quel était son capital ?
Si f(x) = 3,15 alors x = .
Des intérêts de € sont produits par un capital de €.

a. Les intérêts représentent 4,5 % de 50 € soit, en €, 4,5 × 50 ÷ 100.

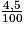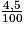b. Les intérêts représentent 4,5 % de x soit $\frac{4,5}{100}$ × x.

c. 3,15 = 0,045 × x donc x = 3,15 ÷ 0,045.