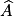Démontrer que tg A = sin A/cos A
Dans un triangle ABC rectangle en B, on a : tg 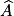 =
= 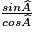 .
.
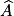 =
= 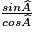 .
.On sait que : tg 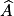 =
= 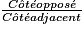 =
= 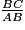 .
.
cos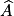 =
= 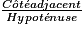 =
= 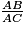
sin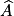 =
= 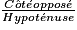 =
= 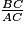
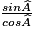 =
= 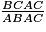 =
= 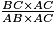 =
= 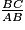 = tg
= tg 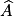
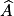 =
= 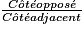 =
= 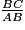 .
.cos
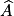 =
= 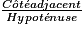 =
= 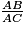
sin
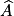 =
= 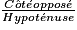 =
= 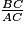
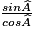 =
= 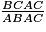 =
= 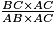 =
= 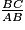 = tg
= tg 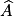
© 2000-2025, Miscellane
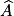 =
= 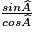 .
.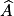 =
= 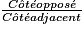 =
= 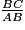 .
.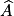 =
= 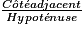 =
= 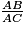
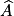 =
= 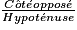 =
= 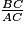
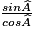 =
= 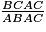 =
= 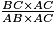 =
= 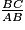 = tg
= tg