Calculer la mesure d'un angle dans un triangle rectangle
Fiche
Si on connaît deux côtés d'un triangle rectangle, on peut calculer la mesure des trois angles.
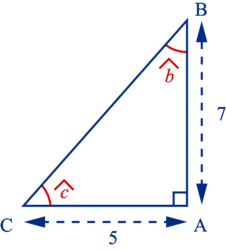
Soit ABC un triangle rectangle en A.
On donne : [AB] = 7 et [AC] = 5.
On veut calculer la mesure des angles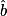
et 
.
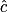Ici, on connaît [AC], le côté opposé à l'angle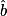
et [AB], le côté adjacent à l'angle 
.
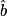On va donc utiliser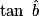
pour calculer 
.
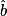On donne : [AB] = 7 et [AC] = 5.
On veut calculer la mesure des angles
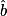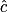et .Ici, on connaît [AC], le côté opposé à l'angle
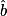et [AB], le côté adjacent à l'angle 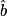.On va donc utiliser
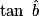pour calculer . |
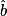• Calcul de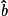 
:
On a :![\mathbf{\tan~\hat{\textit{b}}~=~\frac{[AC]}{[AB]}~=~\frac{5}{7}}](https://static1.assistancescolaire.com/3/images/3mtr07_m8.png)
.
On obtient la valeur de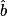
en utilisant la fonction inv tan de la calculatrice.
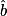= 35° (à un degré près par défaut).
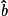:On a :
.On obtient la valeur de
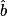en utilisant la fonction inv tan de la calculatrice. 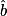= 35° (à un degré près par défaut).• Calcul de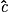 
:
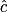= 90° – 35° car la somme des angles d'un triangle est 180°.
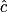= 55°
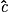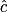: = 90° – 35° car la somme des angles d'un triangle est 180°. 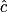= 55°© 2000-2025, Miscellane