Calculer la longueur d'un côté dans un triangle rectangle
Fiche
Si on connaît un angle et un côté d'un triangle rectangle, on peut calculer les autres côtés.
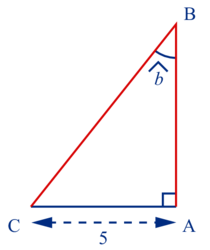
Soit ABC un triangle rectangle en A.
On donne :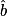 = 30° et AC = 5.
= 30° et AC = 5.
On veut calculer BC et AB.
[AC] étant le côté opposé à l'angle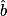 , on peut calculer BC avec
, on peut calculer BC avec 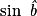 ; puis calculer AB avec
; puis calculer AB avec 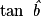
On donne :
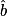 = 30° et AC = 5.
= 30° et AC = 5.On veut calculer BC et AB.
[AC] étant le côté opposé à l'angle
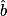 , on peut calculer BC avec
, on peut calculer BC avec 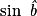 ; puis calculer AB avec
; puis calculer AB avec 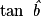
 |
• Calcul de BC :
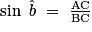 ; donc
; donc 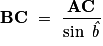
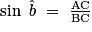 ; donc
; donc 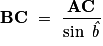
BC = 5 ÷ sin 30° = 5 ÷ 0,5 = 10
• Calcul de AB :
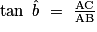 ; donc
; donc 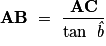
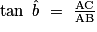 ; donc
; donc 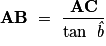
AB = 5 ÷ tan 30° = 8,66
© 2000-2025, Miscellane