Définir une homothétie

Fiche

Définition d'une homothétie

L'image M' du point M du plan par une homothétie de centre O et de rapport k (non nul) est défini par :

OM' = k×OM ;
si k > 0, M' 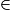$\in$ [OM) (M et M' sont du même côté par rapport à O) ;
si k < 0, M' 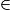$\in$ [MO) (M et M' sont de part et d'autre de O).

Le point M' est l'image du point M par l'homothétie de centre O et de rapport −2.

Propriétés d'une homothétie

L'homothétie de centre O et de rapport −1 est la symétrie de centre O.
Une homothétie conserve l'alignement, le parallélisme et les angles.
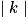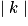Une homothétie multiplie les longueurs par $\mid k\mid$ : si $\mid k\mid$ > 1, l'image d'une figure est un agrandissement de cette figure et, si 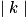$\mid k\mid$ < 1, l'image d'une figure est une réduction de cette figure.
Une homothétie de rapport k transforme un segment [AB] en un segment de longueur 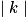$\mid k\mid$ AB.
Une homothétie de rapport k multiplie les aires par k².

Lien avec le théorème de Thalès

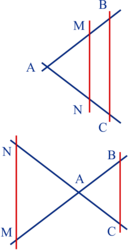
Soit h l'homothétie de centre A et de rapport k et, B et C deux points du plan d'image respective M et N par cette homothétie.
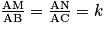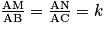Les points A, B, C, M et N forment une configuration de Thalès car $\frac{\mathrm{AM}}{\mathrm{AB}} = \frac{\mathrm{AN}}{\mathrm{AC}} = k$ .

Si k > 0, c'est la configuration de la figure 1 et, si k < 0, c'est la configuration de la figure 2.