Construire un arbre de probabilité
Fiche
On peut visualiser toutes les issues possibles d'une expérience aléatoire à l'aide d'un arbre, appelé arbre des possibles.
Exemples
• On lance une pièce de monnaie et on regarde la face supérieure.
Les issues possibles de cette expérience aléatoire sont : pile, face.
On peut construire un arbre pour visualiser les issues :
Les issues possibles de cette expérience aléatoire sont : pile, face.
On peut construire un arbre pour visualiser les issues :
 |
• Dans une roue équilibrée, la partie verte occupe la moitié du disque et les parties bleue, rouge et beige occupent respectivement 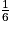 .
.
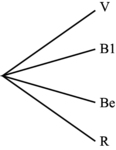
Les issues possibles sont V : verte ; Bl : bleue ; Be : beige et R : rouge.
L'arbre des possibles est donc :
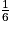 .
.Les issues possibles sont V : verte ; Bl : bleue ; Be : beige et R : rouge.
L'arbre des possibles est donc :
 |
• On peut indiquer sur chaque branche de l'arbre les probabilités des événements, l'arbre est alors un arbre pondéré.
Par exemple, pour la roue, on a :
Par exemple, pour la roue, on a :
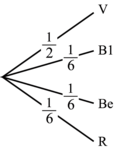 |
Remarque : la somme des probabilités est égale à 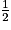 +
+ 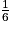 +
+ 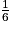 +
+ 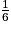 =
= 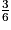 +
+ 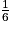 +
+ 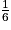 +
+ 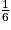 = 1.
= 1.
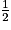 +
+ 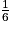 +
+ 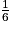 +
+ 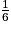 =
= 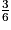 +
+ 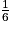 +
+ 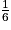 +
+  = 1.
= 1.• En utilisant la roue précédente, on considère l'événement R : « obtenir la couleur rouge ».
L'événement contraire noté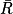 est : « ne pas obtenir la couleur rouge ».
est : « ne pas obtenir la couleur rouge ».
On veut calculer la probabilité de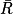 . On a deux méthodes :
. On a deux méthodes :
1. En utilisant l'arbre pondéré, on additionne toutes les probabilités, sauf la probabilité de l'événement R :
p(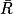 ) =
) = 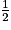 +
+ 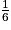 +
+ 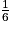 +
+ 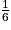 =
= 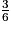 +
+ 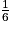 +
+ 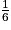 =
= 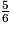 .
.
2. On sait que p(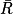 ) = 16 et p(
) = 16 et p(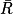 ) + p(
) + p(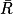 ) = 1
) = 1
Donc p(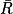 ) = 1 −
) = 1 − 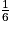 =
= 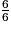 −
− 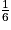 =
= 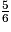 .
.
L'événement contraire noté
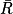 est : « ne pas obtenir la couleur rouge ».
est : « ne pas obtenir la couleur rouge ».On veut calculer la probabilité de
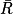 . On a deux méthodes :
. On a deux méthodes :1. En utilisant l'arbre pondéré, on additionne toutes les probabilités, sauf la probabilité de l'événement R :
p(
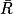 ) =
) = 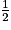 +
+ 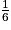 +
+ 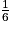 +
+ 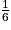 =
= 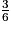 +
+ 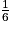 +
+ 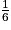 =
= 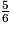 .
.2. On sait que p(
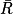 ) = 16 et p(
) = 16 et p(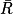 ) + p(
) + p(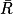 ) = 1
) = 1Donc p(
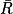 ) = 1 −
) = 1 − 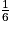 =
= 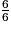 −
− 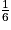 =
= 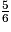 .
.© 2000-2025, Miscellane