Rendre irréductible une fraction

Fiche

Définition

Une fraction est irréductible lorsque son numérateur et son dénominateur n'ont aucun diviseur commun (autre que 1).
Pour rendre irréductible une fraction, on simplifie le numérateur et le dénominateur par leur(s) diviseur(s) commun(s). Pour cela, on peut utiliser la décomposition en produits de facteurs premiers du numérateur et du dénominateur.

Exemples

Exemple 1

Rendre irréductible la fraction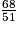 $\frac{68}{51}$ .
On décompose 68 et 51 en produits de facteurs premiers.
68 = 2 × 34 = 2 × 2 × 17 = 2² × 17 et 51 = 3 × 17.
On a donc 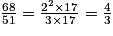$\frac{68}{51}=\frac{2^2\times 17}{3\times 17} =\frac{4}{3}$ , qui est une fraction irréductible.

Exemple 2

La fraction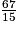 $\frac{67}{15}$ est-elle irréductible ?
15 = 3 × 5 et on remarque que 67 n’est divisible ni par 3, ni par 5.
Les nombres 15 et 67 n'ont donc aucun diviseur commun autre que 1, donc la fraction 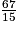$\frac{67}{15}$ est irréductible.

Exemple 3

La fraction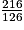 $\frac{216}{126}$ est-elle irréductible ? Si ce n'est pas le cas, la rendre irréductible en détaillant les calculs.
216 et 126 sont divisibles par 2 donc la fraction n'est pas irréductible.
On décompose 216 et 126 en produits de facteurs premiers.
216 = 2 × 108 = 2 × 2 × 54 = 2 × 2 × 2 × 27 = 2 × 2 × 2 × 3 × 9 = 2 × 2 × 2 × 3 × 3 × 3 = 2³ × 3³.
126 = 2 × 63 = 2 × 3 × 21 = 2 × 3 × 3 × 7 = 2 × 3² × 7.
On a donc 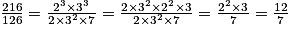$\frac{216}{126}=\frac{2^3 \times 3^3}{2\times 3^2 \times 7}=\frac{2\times 3^2 \times 2^2 \times 3}{2\times 3^2 \times 7}=\frac{2^2 \times 3}{7}=\frac{12}{7}$ qui est une fraction irréductible.