Se ramener à une équation du type (ax + b)(cx+ d) = 0
Fiche
Pour obtenir une équation du type : (ax + b)(cx + d) = 0, on doit :
- passer tous les termes non nuls à gauche du signe égal ;
- factoriser le membre de gauche.
Exemple 1
(E) : 81x2 – (x + 2)2 = 0
• On reconnaît dans le membre de gauche la différence de deux carrés.
On factorise donc en utilisant :
a2 – b2 = (a + b)(a – b).
a2 – b2 = (a + b)(a – b).
(E) : (9x + x + 2)(9x – x – 2) = 0
• On est ramené à une équation produit que l'on sait résoudre.
(E) admet deux solutions :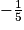 et
et 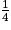 .
.
(E) admet deux solutions :
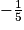 et
et 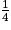 .
.Exemple 2
(E) : x2 – 9 = 2(x + 3)2
• On passe à gauche du signe égal tous les termes non nuls.
(E) : x2 – 9 – 2(x + 3)2 = 0
(E) : x2 – 9 – 2(x + 3)2 = 0
• On factorise la différence de deux carrés x2 – 9 ; on met ainsi en évidence le facteur commun (x + 3).
(E) : (x – 3)(x + 3) – 2(x + 3)2 = 0
(E) : (x + 3) [x – 3 – 2(x + 3)] = 0
(E) admet deux solutions : –3 et –9.
© 2000-2025, Miscellane