Résoudre une équation du type (ax + b)(cx+ d) = 0
Fiche
Règle
Un produit de facteur est nul lorsque l'un des facteurs est nul.(ax + b) (cx + d) est le produit du facteur (ax + b) par le facteur (cx + d).
Ce produit est donc nul lorsque ax + b = 0 ou cx + d = 0.
Exemples
• Résoudre l'équation (E) : 3x(2x + 6) = 0.
3x(2x + 6) est un produit de facteurs : les facteurs sont 3x et (2x + 6).
Donc 3x(2x + 6) = 0 lorsque 3x = 0 ou 2x + 6 = 0.
C'est-à-dire x = 0 ou x = -3.
L'équation (E) admet deux solutions : 0 et -3.
3x(2x + 6) est un produit de facteurs : les facteurs sont 3x et (2x + 6).
Donc 3x(2x + 6) = 0 lorsque 3x = 0 ou 2x + 6 = 0.
C'est-à-dire x = 0 ou x = -3.
L'équation (E) admet deux solutions : 0 et -3.
• Attention, il faut parfois commencer par factoriser.
Ainsi, l'équation 9x2 − 16 = 0 peut s'écrire : (3x − 4)(3x + 4) = 0.
(3x − 4)(3x + 4) est un produit de facteurs : les facteurs sont (3x − 4) et (3x + 4).
Donc 9x2 − 16 = 0 lorsque 3x − 4 = 0 ou 3x + 4 = 0.
C'est-à-dire x =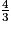 ou x =
ou x = 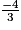 .
.
L'équation 9x2 − 16 = 0 admet deux solutions :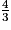 et
et 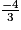 .
.
Ainsi, l'équation 9x2 − 16 = 0 peut s'écrire : (3x − 4)(3x + 4) = 0.
(3x − 4)(3x + 4) est un produit de facteurs : les facteurs sont (3x − 4) et (3x + 4).
Donc 9x2 − 16 = 0 lorsque 3x − 4 = 0 ou 3x + 4 = 0.
C'est-à-dire x =
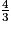 ou x =
ou x = 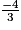 .
.L'équation 9x2 − 16 = 0 admet deux solutions :
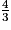 et
et 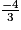 .
.© 2000-2026, Miscellane