Reconnaître un agrandissement ou une réduction

Fiche

Propriété

Lorsqu'on passe d'une figure à une autre par un agrandissement ou une réduction :

les longueurs des côtés sont multipliées par un même nombre k (l'échelle) ;
les angles sont conservés.

Cas d'un triangle

Pour contrôler qu'un triangle est l'agrandissement ou la réduction d'un autre triangle, il suffit de s'assurer que l'une des deux conditions (sur les longueurs ou sur les angles) est vérifiée.

Exemple :
On a (MN) // (BC) ;
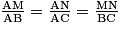
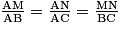
d'où $\frac{\mathrm{AM}}{\mathrm{AB}} = \frac{\mathrm{AN}}{\mathrm{AC}} = \frac{\mathrm{MN}}{\mathrm{BC}}$

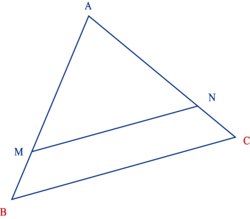Reconnaître un agrandissement ou une réduction - illustration 1

Autrement dit, les longueurs des côtés des triangles AMN et ABC sont proportionnelles.
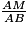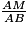On peut donc dire que le triangle AMN est une réduction du triangle ABC ; l'échelle de réduction est égale à $\frac{AM}{AB}$ .