Vision et image
Fiche
Les hommes se sont toujours intéressés à la lumière, en observant le Soleil et le feu qui éclairent et qui chauffent. La lumière est en effet indispensable à la perception du monde qui nous entoure. Son étude a permis d'expliquer les arcs-en-ciel, la couleur des étoiles ou leur composition, mais également de corriger les défauts de l'œil, ou de mesurer la distance Terre-Lune.
I. La propagation de la lumière
• La lumière se propage en ligne droite dans le vide et dans les milieux matériels transparents et homogènes : ce phénomène est appelé la propagation rectiligne de la lumière.
• Le trajet suivi par la lumière n'est pas visible, on modélise ce trajet par un rayon lumineux qui est une droite orientée par une flèche partant de la source de lumière et indiquant la direction et le sens de propagation de la lumière.
• Dans le vide, la vitesse de la lumière, appelée célérité et notée c, est égale à c = 3,00·108 m·s−1. Dans l'air, la vitesse de propagation de la lumière a quasiment la même valeur. Cette valeur est très grande devant celle du son dans l'air v = 343 m·s−1 ou celle d'un TGV qui est d'environ v = 100 m·s−1 ou même celle d'une fusée au décollage dont la vitesse est v = 1 000 m·s−1.
• On appelle indice de réfraction n d'un milieu transparent homogène le rapport entre la célérité de la lumière dans le vide c et la vitesse de propagation dans le milieu considéré : 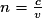 .
.
Exemple pour l'air n = 1,00, pour l'eau n = 1,33.
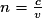 .
.Exemple pour l'air n = 1,00, pour l'eau n = 1,33.
II. La dispersion de la lumière
• Un prisme ou un réseau permettent de décomposer un faisceau de lumière blanche.
• On appelle dispersion d'une lumière la séparation des différentes radiations qui composent la lumière.
• La lumière blanche est composée d'une infinité de couleurs, appelée radiations lumineuses. Chaque radiation lumineuse est caractérisée par sa longueur d'onde λ (lambda) qui s'exprime en mètres (m). La lumière blanche est donc polychromatique alors que chaque radiation lumineuse sera une radiation monochromatique.
• Le prisme dévie davantage les radiations violet/bleu que les radiations orange/rouge. Il dévie davantage les courtes longueurs d'onde.
• Le Soleil est une source de lumière blanche.
III. Spectres du rayonnement émis par un corps chaud et spectres de raies d'émission
• La lumière visible s'étend d'une longueur d'onde égale à 400 nm (violet) jusqu'à 750 nm (rouge). Le nanomètre (nm) correspond à un sous-multiple du mètre : 1 nm = 1  10−9m.
10−9m.
 10−9m.
10−9m.• On appelle spectre l'apparence de la lumière émise par un corps lorsqu'elle est dispersée (séparée) par un prisme.
• Un corps chauffé émet de la lumière. Le spectre de cette lumière est continu et les radiations émises dépendent de la température de surface de ce corps. Plus sa température de surface est grande et plus le spectre émis s'enrichit vers le violet et la couleur de la lumière émise évolue du rouge au blanc, puis au blanc bleuté. La détermination de la couleur émise permet ainsi de déterminer la température de surface des étoiles.
• Un gaz d'atomes excités grâce à des décharges électriques émet de la lumière lors de leur désexcitation. On n'observe qu'un nombre restreint de raies colorées sur fond noir. Ce spectre est appelé spectre de raies d'émission et est caractéristique de l'espèce. On peut ainsi identifier les identités chimiques produisant la lumière.
IV. Réflexion et réfraction
• Lorsqu'un rayon lumineux passe d'un milieu transparent dans un autre, sa direction change à la surface de séparation : ce phénomène est appelé réfraction. Une partie de la lumière est réfléchie : ce phénomène est appelé la réflexion.
• Les lois de Snell-Descartes permettent de rendre comptent de la réflexion et de la réfraction.
La réflexion et la réfraction
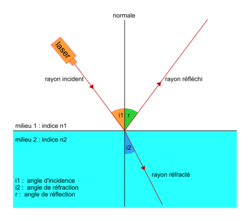 |
1re loi de Snell-Descartes : le rayon réfracté, le rayon incident et la normale appartiennent au même plan.
2e loi de Snell-Descartes sur la réflexion : les angles d'incidence i1 et de réflexion r sont égaux : i1 = r.
3e loi de Snell-Descartes sur la réfraction : les angles d'incidence i1 et de réfraction i2 sont reliés par la relation : n1.sin(i1) = n2.sin(i2) où n1 est l'indice de réfraction du milieu 1 et n2 est l'indice de réfraction du milieu 2.
2e loi de Snell-Descartes sur la réflexion : les angles d'incidence i1 et de réflexion r sont égaux : i1 = r.
3e loi de Snell-Descartes sur la réfraction : les angles d'incidence i1 et de réfraction i2 sont reliés par la relation : n1.sin(i1) = n2.sin(i2) où n1 est l'indice de réfraction du milieu 1 et n2 est l'indice de réfraction du milieu 2.
V. Lentilles convergentes
• Une lentille est constituée d'un milieu transparent possédant au moins une face non plane. On appelle lentilles convergentes celles qui sont minces sur les bords et épaisses au centre.
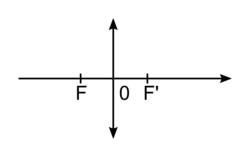
• Dans le cadre du modèle des lentilles minces, les lentilles sont représentées par une double flèche de part et d'autre d'un point O appelé centre optique de la lentille. Chaque lentille est caractérisée par son foyer objet F et son foyer image 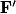 symétrique l'un de l'autre par rapport à O.
symétrique l'un de l'autre par rapport à O.
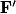 symétrique l'un de l'autre par rapport à O.
symétrique l'un de l'autre par rapport à O.Foyer objet et foyer image
 |
• La distance focale 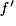 correspond à la distance entre O et
correspond à la distance entre O et 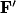 .
.
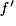 correspond à la distance entre O et
correspond à la distance entre O et 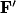 .
.• Pour construire graphiquement l'image d'un objet, on utilise trois rayons particuliers :
- Tout rayon passant par le centre optique O n'est pas dévié.
- Tout rayon passant par le foyer objet F ressort parallèlement à l'axe optique.
- Tout rayon arrivant parallèlement à l'axe optique ressort en passant par le foyer image
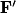 .
.
Construction graphique de l'image d'un objet
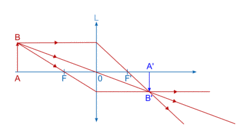 |
• L'image 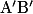 est réelle, car elle est visible sur un écran et renversée.
est réelle, car elle est visible sur un écran et renversée.
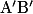 est réelle, car elle est visible sur un écran et renversée.
est réelle, car elle est visible sur un écran et renversée.• La valeur absolue du grandissement γ de la lentille est donnée par le rapport entre la taille de l'image et la taille de l'objet, ou la distance du centre optique à l'image et la distance du centre optique à l'objet.
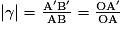
Si |γ| > 1 alors l'image sera plus grande que l'objet et si |γ| < 1 alors l'image sera plus petite que l'objet.
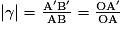
Si |γ| > 1 alors l'image sera plus grande que l'objet et si |γ| < 1 alors l'image sera plus petite que l'objet.
• On peut modéliser l'œil par :
- une lentille convergente pour le cristallin et les milieux transparents ;
- un diaphragme pour l'iris ;
- un écran pour la rétine.
À retenir :
Décrire et expliquer la propagation rectiligne de la lumière.
Savoir citer la valeur de la vitesse de la lumière dans le vide ou dans l'air et savoir la comparer à d'autres valeurs de vitesse couramment rencontrées.
Savoir ce qu'est la lumière blanche et ce qu'est la lumière colorée.
Savoir caractériser le spectre du rayonnement émis par un corps chaud.
Savoir caractériser un rayonnement monochromatique par sa longueur d'onde dans le vide ou dans l'air.
Savoir exploiter un spectre de raies.
Connaître et savoir exploiter les lois de Snell-Descartes pour la réflexion et la réfraction.
Connaître la définition de l'indice optique d'un milieu matériel.
Décrire et expliquer qualitativement le phénomène de dispersion de la lumière par un prisme (ou un réseau).
Décrire et expliquer le modèle de la lentille mince convergente. Connaître les notions de foyer, distance focale, image réelle.
Savoir caractériser les foyers d'une lentille mince convergente à l'aide du modèle du rayon lumineux.
Savoir utiliser le modèle du rayon lumineux pour déterminer graphiquement la position, la taille et le sens de l'image réelle d'un objet-plan réel donnée par une lentille convergente.
Savoir définir et déterminer géométriquement un grandissement.
Savoir modéliser l'œil.
Décrire et expliquer la propagation rectiligne de la lumière.
Savoir citer la valeur de la vitesse de la lumière dans le vide ou dans l'air et savoir la comparer à d'autres valeurs de vitesse couramment rencontrées.
Savoir ce qu'est la lumière blanche et ce qu'est la lumière colorée.
Savoir caractériser le spectre du rayonnement émis par un corps chaud.
Savoir caractériser un rayonnement monochromatique par sa longueur d'onde dans le vide ou dans l'air.
Savoir exploiter un spectre de raies.
Connaître et savoir exploiter les lois de Snell-Descartes pour la réflexion et la réfraction.
Connaître la définition de l'indice optique d'un milieu matériel.
Décrire et expliquer qualitativement le phénomène de dispersion de la lumière par un prisme (ou un réseau).
Décrire et expliquer le modèle de la lentille mince convergente. Connaître les notions de foyer, distance focale, image réelle.
Savoir caractériser les foyers d'une lentille mince convergente à l'aide du modèle du rayon lumineux.
Savoir utiliser le modèle du rayon lumineux pour déterminer graphiquement la position, la taille et le sens de l'image réelle d'un objet-plan réel donnée par une lentille convergente.
Savoir définir et déterminer géométriquement un grandissement.
Savoir modéliser l'œil.
© 2000-2025, Miscellane