La cinématique du point s'intéresse à l'étude des mouvements. Pour décrire un mouvement, il faut être vigilant sur la définition du système étudié et du référentiel d'étude. Plusieurs types de mouvement existent, mais chacun d'eux a ses propres caractéristiques en matière de trajectoire et de vitesse.
I. Le système et le référentiel
• On appelle système l'objet dont on étudie le mouvement. On le note parfois entre accolades { }.
Exemple : pour l'étude du mouvement d'une voiture, le système est la voiture. On peut le noter {voiture}.
Exemple : pour l'étude du mouvement d'une voiture, le système est la voiture. On peut le noter {voiture}.
• Le mouvement de l'objet sera décrit par rapport à un objet de référence : le référentiel. On associe au référentiel, un repère d'espace pour indiquer les positions successives du système et une horloge qui permet d'associer les dates.
- Le mouvement de la Lune sera décrit par rapport au référentiel géocentrique (centré sur la Terre).
- Le mouvement du cycliste sera décrit par rapport au référentiel terrestre (objet fixe à la surface de la Terre).
• Le choix de l'échelle temporelle et de l'échelle spatiale doit être pertinent pour décrire au mieux le mouvement.
Exemple : pour décrire le mouvement de la Lune autour de la Terre, on choisira le mois et le kilomètre. Le choix des millions d'années et du centimètre est non adapté.
Exemple : pour décrire le mouvement de la Lune autour de la Terre, on choisira le mois et le kilomètre. Le choix des millions d'années et du centimètre est non adapté.
II. Relativité du mouvement
• La trajectoire d'un système est l'ensemble des positions prises par le système au cours du temps. Il existe plusieurs types de trajectoires :
- Si la trajectoire est une droite, on dira que le mouvement est rectiligne.
- Si la trajectoire est un cercle, on dira que le mouvement est circulaire.
- Si la trajectoire est quelconque, on dira que le mouvement est curviligne.
• Un solide est animé d'un mouvement de translation lorsque tout segment joignant deux points quelconques de ce solide reste parallèle à lui-même, c'est-à-dire si, à chaque instant, tous ses points ont la même vitesse.
Exemple de mouvement de translation : le mouvement de la nacelle dans la grande roue est un mouvement de translation circulaire.
Exemple de mouvement de translation : le mouvement de la nacelle dans la grande roue est un mouvement de translation circulaire.
• Selon le référentiel choisi, le système peut être mobile ou immobile. Par exemple, un homme assis dans un train qui roule est en mouvement par rapport aux arbres qui bordent les rails, mais est immobile par rapport au train. On dit que le mouvement est relatif.
III. Modélisation du système
• Pour simplifier l'étude du mouvement d'un système, on ramène le système à un point auquel on associe la masse du système. Ce point est appelé point matériel. Le point choisi est le plus souvent le centre de gravité du système. Cette simplification de l'étude entraîne une perte d'informations (la rotation de celui-ci, les frottements…).
Exemple : pour étudier le mouvement d'un ballon de rugby, on le modélise par son centre de gravité, mais on négligera la rotation du ballon sur lui-même.
Exemple : pour étudier le mouvement d'un ballon de rugby, on le modélise par son centre de gravité, mais on négligera la rotation du ballon sur lui-même.
• La trajectoire du point matériel sera représentée par une courbe orientée selon le sens du mouvement. Elle représente les positions successives occupées par ce point au cours du mouvement.
IV. La vitesse
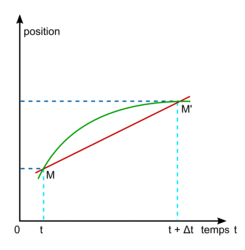
• Entre les instants t et t + Δt, le mobile se déplace de M en 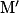 suivant un vecteur déplacement
suivant un vecteur déplacement 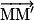 . Ce vecteur a pour caractéristiques :
. Ce vecteur a pour caractéristiques :
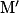 suivant un vecteur déplacement
suivant un vecteur déplacement 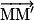 . Ce vecteur a pour caractéristiques :
. Ce vecteur a pour caractéristiques : - direction : selon la droite
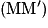 ;
; - sens : de M vers
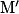 ;
; - intensité : la longueur du segment
![[\mathrm{M{M}}']](https://static1.assistancescolaire.com/2/images/2_ph_06_m5.png) .
.
 |
• On appelle vecteur vitesse moyenne le rapport du vecteur déplacement 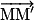 par la durée Δt du parcours :
par la durée Δt du parcours :
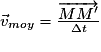 .
.
Exemple : pour un trajet de 100 km durant 2 h, la vitesse moyenne est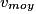 = 50 km
= 50 km h-1.
h-1.
L'unité de la vitesse moyenne dans le système international est le mètre par seconde (m s-1).
s-1).
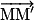 par la durée Δt du parcours :
par la durée Δt du parcours :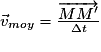 .
.Exemple : pour un trajet de 100 km durant 2 h, la vitesse moyenne est
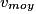 = 50 km
= 50 km h-1.
h-1.L'unité de la vitesse moyenne dans le système international est le mètre par seconde (m
 s-1).
s-1).• Il est parfois nécessaire de convertir les kilomètres par heure en mètres par seconde et inversement. Pour passer de l'un à l'autre, il suffit de multiplier ou diviser par 3,6.
Exemple : ainsi si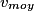 = 50 km
= 50 km  h-1 alors
h-1 alors 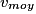 = 50/3,6= 13,9 m
= 50/3,6= 13,9 m  s-1.
s-1.
Exemple : ainsi si
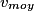 = 50 km
= 50 km  h-1 alors
h-1 alors 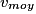 = 50/3,6= 13,9 m
= 50/3,6= 13,9 m  s-1.
s-1.• Si la durée de parcours Δt est extrêmement petite, la vitesse moyenne sera appelée vitesse en un point et sera définie par la relation :
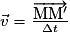 .
.
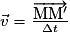 .
.Approximation du vecteur vitesse en un point
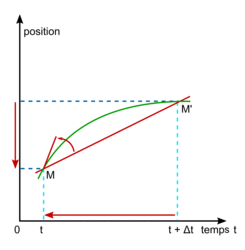 |
Ce vecteur a les caractéristiques suivantes :
- direction : tangent à la trajectoire ;
- sens : le même que celui du mouvement ;
- intensité : celle de la vitesse en m
 s-1 ;
s-1 ; - point d'application : au point considéré.
Représentation de deux vecteurs vitesse
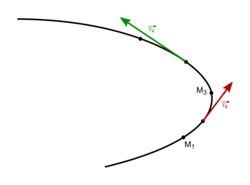 |
• En pratique, pour représenter le vecteur vitesse 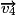 au point M4, avec une échelle de 1 cm pour 1 m
au point M4, avec une échelle de 1 cm pour 1 m  s-1, il faut :
s-1, il faut :
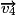 au point M4, avec une échelle de 1 cm pour 1 m
au point M4, avec une échelle de 1 cm pour 1 m  s-1, il faut :
s-1, il faut : - mesurer la distance M4M5 ;
- convertir la distance M4M5 en mètres ;
- calculer
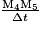 en m
en m  s-1 ;
s-1 ; - faire un segment fléché partant de M4, tangent à la trajectoire, de même sens que le mouvement et de longueur proportionnelle à l'échelle qui sera donnée.
V. Cas du mouvement rectiligne
• Il faut s'intéresser à la variation du vecteur vitesse pour pouvoir qualifier un mouvement rectiligne. Si on appelle 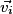 la vitesse à un instant i et
la vitesse à un instant i et 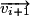 la vitesse à l'instant i+1, alors la variation du vecteur vitesse est donnée par :
la vitesse à l'instant i+1, alors la variation du vecteur vitesse est donnée par : 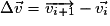 .
.
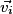 la vitesse à un instant i et
la vitesse à un instant i et 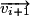 la vitesse à l'instant i+1, alors la variation du vecteur vitesse est donnée par :
la vitesse à l'instant i+1, alors la variation du vecteur vitesse est donnée par : 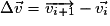 .
.• Si la variation du vecteur vitesse est nulle, alors le vecteur vitesse reste constant (en direction, en sens et en valeur) : le mouvement sera dit rectiligne uniforme.
Exemple de mouvement rectiligne uniforme :
La vitesse reste constante :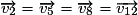 .
.
Exemple de mouvement rectiligne uniforme :
La vitesse reste constante :
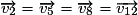 .
.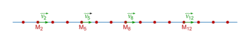 |
• Si la variation du vecteur vitesse diminue, alors la valeur du vecteur vitesse diminue : le mouvement sera dit rectiligne non uniforme (il sera retardé ou ralenti).
Exemple de mouvement rectiligne où la variation du vecteur vitesse diminue : la variation du vecteur vitesse diminue et la valeur du vecteur vitesse diminue.
Exemple de mouvement rectiligne où la variation du vecteur vitesse diminue : la variation du vecteur vitesse diminue et la valeur du vecteur vitesse diminue.
 |
• Si la variation du vecteur vitesse augmente, alors la valeur du vecteur vitesse augmente : le mouvement sera dit rectiligne non uniforme (il sera accéléré).
Exemple de mouvement rectiligne où la variation du vecteur vitesse augmente :la variation du vecteur vitesse augmente et la valeur du vecteur vitesse augmente.
Exemple de mouvement rectiligne où la variation du vecteur vitesse augmente :la variation du vecteur vitesse augmente et la valeur du vecteur vitesse augmente.
 |
À retenir :
Savoir définir et identifier un système.
Savoir identifier les échelles temporelles et spatiales pertinentes de description d'un mouvement.
Savoir définir et choisir un référentiel pour décrire le mouvement d'un système.
Savoir expliquer dans le cas de la translation, l'influence du choix du référentiel sur la description du mouvement d'un système.
Décrire le mouvement d'un système par celui d'un point et caractériser cette modélisation en termes de perte d'informations.
Savoir définir la position et caractériser différentes trajectoires.
Savoir définir le vecteur déplacement d'un point.
Savoir définir le vecteur vitesse moyenne d'un point.
Approcher le vecteur vitesse d'un point à l'aide du vecteur vitesse moyenne d'un point à l'aide du vecteur déplacement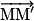 et savoir le représenter.
et savoir le représenter.
Savoir caractériser un mouvement rectiligne uniforme ou non uniforme.
Savoir définir le vecteur variation du vecteur vitesse.
Savoir définir et identifier un système.
Savoir identifier les échelles temporelles et spatiales pertinentes de description d'un mouvement.
Savoir définir et choisir un référentiel pour décrire le mouvement d'un système.
Savoir expliquer dans le cas de la translation, l'influence du choix du référentiel sur la description du mouvement d'un système.
Décrire le mouvement d'un système par celui d'un point et caractériser cette modélisation en termes de perte d'informations.
Savoir définir la position et caractériser différentes trajectoires.
Savoir définir le vecteur déplacement d'un point.
Savoir définir le vecteur vitesse moyenne d'un point.
Approcher le vecteur vitesse d'un point à l'aide du vecteur vitesse moyenne d'un point à l'aide du vecteur déplacement
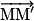 et savoir le représenter.
et savoir le représenter.Savoir caractériser un mouvement rectiligne uniforme ou non uniforme.
Savoir définir le vecteur variation du vecteur vitesse.
Exercice n°1
Dans quelle situation le référentiel donné est-il le plus adapté pour décrire le mouvement du système ?
Cochez la bonne réponse.
| ||
| ||
|
Le mouvement de la Lune est décrit par rapport au centre de la Terre : le référentiel le plus adapté est le référentiel géocentrique. Le mouvement d'un cycliste sur la Terre doit être étudié dans le référentiel lié au sol, c'est-à-dire le référentiel terrestre. Le mouvement du ballon de rugby se fera également dans le référentiel lié au sol, on pourra ainsi choisir un spectateur qui est immobile dans ce référentiel terrestre.
Exercice n°2
On considère un passager A assis dans un train en mouvement et un passager B qui marche dans le train. Une dame regarde passer le train au bord des rails. Quelle proposition est vraie ?
Cochez la bonne réponse.
| ||
| ||
|
Le passager A est assis dans le train : il est donc immobile par rapport au train. Le passager B est dans le train qui est en mouvement par rapport à la dame : il est en mouvement par rapport à la dame. Par contre le passager B est en mouvement par rapport au passager A qui est assis : donc pour le passager B, c'est le passager A qui est en mouvement par rapport à lui.
Exercice n°3
Parmi les propositions suivantes, quelle est celle qui donne la bonne trajectoire ? On considère un cycliste roulant sur une route rectiligne horizontale et un observateur immobile sur le bord de la route.
Cochez la bonne réponse.
| ||
| ||
|
L'observateur immobile peut être considéré comme un référentiel terrestre. Il voit la roue tourner et avancer horizontalement. La valve du pneu du vélo ne peut pas avoir de trajectoire rectiligne ni circulaire dans le référentiel terrestre. Dans le référentiel du vélo, la roue tourne : la valve du pneu du vélo a une trajectoire circulaire.
Exercice n°4
Quelle vitesse moyenne est juste ?
Cochez la bonne réponse.
| ||
| ||
|
Un marathonien a une vitesse 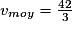 = 14 m
= 14 m  s-1, soit
s-1, soit 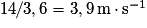 . Pour calculer la vitesse de l'automobiliste, il faut convertir les minutes en heures, sachant que 30 minutes = 0,50 h. La durée du trajet est 2,50 h. Sa vitesse est :
. Pour calculer la vitesse de l'automobiliste, il faut convertir les minutes en heures, sachant que 30 minutes = 0,50 h. La durée du trajet est 2,50 h. Sa vitesse est : 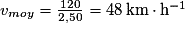 .
.
Pour calculer la vitesse du train, il faut également convertir les minutes en heures :
49 minutes = 49 / 60 = 0,82 heure. La durée du trajet est 2,82 h. Sa vitesse est :
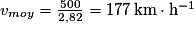 .
.
Il faut ensuite convertir la vitesse en mètre par seconde : 177/3,6= 49,1 m s-1.
s-1.
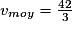 = 14 m
= 14 m  s-1, soit
s-1, soit 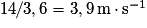 . Pour calculer la vitesse de l'automobiliste, il faut convertir les minutes en heures, sachant que 30 minutes = 0,50 h. La durée du trajet est 2,50 h. Sa vitesse est :
. Pour calculer la vitesse de l'automobiliste, il faut convertir les minutes en heures, sachant que 30 minutes = 0,50 h. La durée du trajet est 2,50 h. Sa vitesse est : 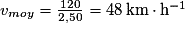 .
. Pour calculer la vitesse du train, il faut également convertir les minutes en heures :
49 minutes = 49 / 60 = 0,82 heure. La durée du trajet est 2,82 h. Sa vitesse est :
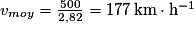 .
.Il faut ensuite convertir la vitesse en mètre par seconde : 177/3,6= 49,1 m
 s-1.
s-1. s-1.
s-1. h-1.
h-1. s-1.
s-1.
