Multiples, diviseurs et nombres premiers
Fiche
I. Nombres entiers
Nombres entiers naturels
• Un entier naturel est un nombre entier qui est positif ou nul (égal à 0). L'ensemble des nombres entiers naturels est noté 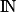 .
.
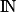 .
.• Exemples : 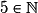 ;
; 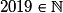 ;
; 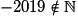
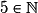 ;
; 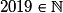 ;
; 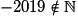
Nombres entiers relatifs
• Un entier relatif est un nombre entier qui est positif, négatif ou nul.
• L'ensemble des nombres entiers relatifs est noté  .
.
 .
.• Exemples : 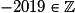 ;
; 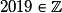 ;
; 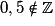
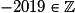 ;
; 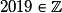 ;
; 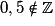
II. Multiples et diviseurs
• Définition : Soit a et b deux entiers. On dit que a est un multiple de b s'il existe un entier k tel que a = k b. On dit alors que b est un diviseur de a.
• Exemples :
2019 est un multiple de 3, car 2019 = k × 3 avec k = 673.
5 est un diviseur de 70, car 70 = k × 5 avec k = 14.
20 n'est pas un multiple de 3 car il n'existe pas d'entier k tel que 20 = k × 3.
2019 est un multiple de 3, car 2019 = k × 3 avec k = 673.
5 est un diviseur de 70, car 70 = k × 5 avec k = 14.
20 n'est pas un multiple de 3 car il n'existe pas d'entier k tel que 20 = k × 3.
• Algorithme : Déterminer si a est un mutiple de b.
 |
• Remarque :
a//b donne le quotient de la division euclidienne de a par b.
a//b donne le quotient de la division euclidienne de a par b.
• Propriété :
La somme de deux multiples d'un entier b est un multiple de b.
La somme de deux multiples d'un entier b est un multiple de b.
• Démonstration :
Soit x et y deux multiples de b.
Comme x est un multiple de b, il existe un entier k1 tel que x = kb
Comme y est un multiple de b, il existe un entier m2 tel que y = mb
Alors : x + y = k b + m b = (k + m)b
Or (k + m) est un entier donc x + y est un multiple de b.
Exercice n°1Exercice n°2
Soit x et y deux multiples de b.
Comme x est un multiple de b, il existe un entier k1 tel que x = kb
Comme y est un multiple de b, il existe un entier m2 tel que y = mb
Alors : x + y = k b + m b = (k + m)b
Or (k + m) est un entier donc x + y est un multiple de b.
Exercice n°1Exercice n°2
III. Nombres pairs et impairs
• Définition :
Un nombre pair est un entier multiple de 2. Un nombre impair est un nombre qui n'est pas pair.
Un nombre pair est un entier multiple de 2. Un nombre impair est un nombre qui n'est pas pair.
• Exemples :
2018, 2020 et 0 sont des nombres pairs.
2019, 11 et 1789 sont des nombres impairs.
2018, 2020 et 0 sont des nombres pairs.
2019, 11 et 1789 sont des nombres impairs.
• Propriétés :
Un nombre pair s'écrit de manière unique sous la forme 2k, avec k entier. Un nombre impair s'écrit de manière unique sous la forme 2k + 1, avec k entier. Le carré d'un nombre impair est impair.
Un nombre pair s'écrit de manière unique sous la forme 2k, avec k entier. Un nombre impair s'écrit de manière unique sous la forme 2k + 1, avec k entier. Le carré d'un nombre impair est impair.
• Démonstration :
Soit a est un nombre impair. Alors il s'écrit sous la forme a = 2k+1, avec k entier.
Alors a2 = (2k + 1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1 = 2m + 1, avec m = 2k2 + 2k.
m est un entier car il est la somme de deux entiers
Ainsi a2 s'écrit sous la forme a = 2m + 1 (avec m entier) donc a2 est impair.
Exercice n°3
Soit a est un nombre impair. Alors il s'écrit sous la forme a = 2k+1, avec k entier.
Alors a2 = (2k + 1)2 = 4k2 + 4k + 1 = 2(2k2 + 2k) + 1 = 2m + 1, avec m = 2k2 + 2k.
m est un entier car il est la somme de deux entiers
Ainsi a2 s'écrit sous la forme a = 2m + 1 (avec m entier) donc a2 est impair.
Exercice n°3
IV. Nombres premiers
• Définition :
Un entier naturel est premier s'il possède exactement deux diviseurs qui sont 1 et lui-même.
Un entier naturel est premier s'il possède exactement deux diviseurs qui sont 1 et lui-même.
• Exemples :
2, 3, 5, 7, 11, 13, 17, 19, 23 sont des nombres premiers.
2, 3, 5, 7, 11, 13, 17, 19, 23 sont des nombres premiers.
• Algorithme :
Déterminer si un nombre entier est premier.
Déterminer si un nombre entier est premier.
 |
• Remarque :
Le nombre 1 n'est pas premier car il ne possède qu'un seul diviseur : lui-même.
Le nombre 1 n'est pas premier car il ne possède qu'un seul diviseur : lui-même.
• Propriété :
Tout nombre non premier se décompose de manière unique en produit de nombres premiers.
Tout nombre non premier se décompose de manière unique en produit de nombres premiers.
• Exemple :
2019 = 673 × 3 ; 1492 = 2 × 2 × 373
2019 = 673 × 3 ; 1492 = 2 × 2 × 373
• Définition :
On dit que deux nombres sont premiers entre eux lorsque leur seul diviseur commun est 1.
On dit qu'une fraction est irréductible, lorsque son numérateur et son dénominateur sont premiers entre eux.
Exercice n°4Exercice n°5
On dit que deux nombres sont premiers entre eux lorsque leur seul diviseur commun est 1.
On dit qu'une fraction est irréductible, lorsque son numérateur et son dénominateur sont premiers entre eux.
Exercice n°4Exercice n°5
© 2000-2025, Miscellane