Équations de droites et systèmes d'équations linéaires
Fiche
La géométrie analytique, inventée par Descartes, associe à tout point ou tout vecteur du plan des coordonnées. Démontrer les propriétés d'une figure revient alors à effectuer des calculs. C'est plus direct et souvent plus convaincant.
On peut ainsi montrer que des droites sont parallèles, que des points sont alignés, que quatre points définissent un parallélogramme, formuler différemment la propriété de Thalès, etc.
À toute droite on peut associer une équation, c'est à dire une relation vérifiée par les coordonnées de chacun de ses points. On sait qu'une fonction affine se représente par une droite. Réciproquement toute droite du plan ne peut représenter une fonction affine. Les droites parallèles à l'axe des ordonnées ne conviennent pas. La forme générale d'une équation de droite n'est donc pas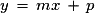 , mais ax + by + c =0
, mais ax + by + c =0 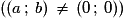 .
.
Le repère nécessaire aux calculs n'est pas toujours fourni, il faut alors définir précédemment une origine et deux vecteurs non nuls et non colinéaires pour que tout point ou tout vecteur du plan ait un couple unique de coordonnées.
On verra par ailleurs qu'un système de deux équations à deux inconnues peut s'interpréter à l'aide d'équations de droites ; en effet, résoudre un tel système revient à chercher les coordonnées d'un point d'intersection de deux droites.
On peut ainsi montrer que des droites sont parallèles, que des points sont alignés, que quatre points définissent un parallélogramme, formuler différemment la propriété de Thalès, etc.
À toute droite on peut associer une équation, c'est à dire une relation vérifiée par les coordonnées de chacun de ses points. On sait qu'une fonction affine se représente par une droite. Réciproquement toute droite du plan ne peut représenter une fonction affine. Les droites parallèles à l'axe des ordonnées ne conviennent pas. La forme générale d'une équation de droite n'est donc pas
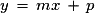 , mais ax + by + c =0
, mais ax + by + c =0 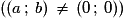 .
.Le repère nécessaire aux calculs n'est pas toujours fourni, il faut alors définir précédemment une origine et deux vecteurs non nuls et non colinéaires pour que tout point ou tout vecteur du plan ait un couple unique de coordonnées.
On verra par ailleurs qu'un système de deux équations à deux inconnues peut s'interpréter à l'aide d'équations de droites ; en effet, résoudre un tel système revient à chercher les coordonnées d'un point d'intersection de deux droites.
1. Comment déterminer une équation de droite ?
• Soit A(xA ; yA) et B(xB ; yB) deux points donnés dans un repère, déterminer une équation de la droite(AB) consiste à chercher une condition qui soit nécessaire et suffisante pour qu'un point M(x ; y) soit aligné avec A et B : cette condition est la colinéarité des vecteurs 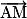 et
et 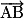 .
.
Le vecteur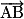 a pour coordonnées (xB − xA ; yB − yA), le vecteur
a pour coordonnées (xB − xA ; yB − yA), le vecteur 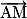 a pour coordonnées (x − xA ; y − yA), la condition de colinéarité s'écrit alors : (x − xA)(yB − yA) = (y − yA)(xB − xA).
a pour coordonnées (x − xA ; y − yA), la condition de colinéarité s'écrit alors : (x − xA)(yB − yA) = (y − yA)(xB − xA).
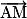 et
et 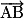 .
.Le vecteur
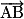 a pour coordonnées (xB − xA ; yB − yA), le vecteur
a pour coordonnées (xB − xA ; yB − yA), le vecteur 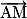 a pour coordonnées (x − xA ; y − yA), la condition de colinéarité s'écrit alors : (x − xA)(yB − yA) = (y − yA)(xB − xA).
a pour coordonnées (x − xA ; y − yA), la condition de colinéarité s'écrit alors : (x − xA)(yB − yA) = (y − yA)(xB − xA).• On distingue deux cas :
– si les points A et B ont la même abscisse k, soit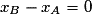 , l'équation réduite de la droite (AB) est alors
, l'équation réduite de la droite (AB) est alors 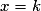 , cette droite est parallèle à l'axe des ordonnées ;
, cette droite est parallèle à l'axe des ordonnées ;
– si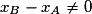 , on peut calculer le coefficient directeur de la droite (AB)
, on peut calculer le coefficient directeur de la droite (AB) 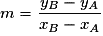 et l'ordonnée à l'origine
et l'ordonnée à l'origine 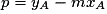 . L'équation de la droite (AB) est alors :
. L'équation de la droite (AB) est alors : 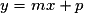 .
.
– si les points A et B ont la même abscisse k, soit
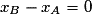 , l'équation réduite de la droite (AB) est alors
, l'équation réduite de la droite (AB) est alors 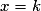 , cette droite est parallèle à l'axe des ordonnées ;
, cette droite est parallèle à l'axe des ordonnées ;– si
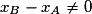 , on peut calculer le coefficient directeur de la droite (AB)
, on peut calculer le coefficient directeur de la droite (AB) 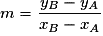 et l'ordonnée à l'origine
et l'ordonnée à l'origine 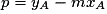 . L'équation de la droite (AB) est alors :
. L'équation de la droite (AB) est alors : 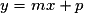 .
.• Réciproquement, dans un repère du plan, l'ensemble des points M de coordonnées (x ; y) tels que 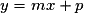 est une droite qui n'est pas parallèle à l'axe des ordonnées.
est une droite qui n'est pas parallèle à l'axe des ordonnées.
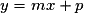 est une droite qui n'est pas parallèle à l'axe des ordonnées.
est une droite qui n'est pas parallèle à l'axe des ordonnées.Exemple
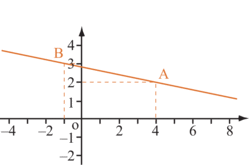 |
Soit les deux points A(4 ; 2) et B(−1 ; 3) et M un point quelconque de coordonnées (x ; y).
On calcule les coordonnées des vecteurs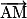 et
et 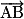 , on obtient
, on obtient 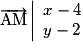 et
et 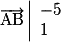 .
.
On écrit alors que M est aligné avec A et B si et seulement si det (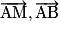 = 0, ce qui se traduit par l'équation
= 0, ce qui se traduit par l'équation 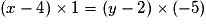 , qui est l'équation de la droite (AB).
, qui est l'équation de la droite (AB).
Après transformation de l'égalité, on obtient l'équation :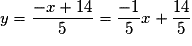 .
.
On calcule les coordonnées des vecteurs
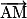 et
et 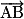 , on obtient
, on obtient 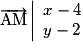 et
et 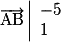 .
.On écrit alors que M est aligné avec A et B si et seulement si det (
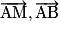 = 0, ce qui se traduit par l'équation
= 0, ce qui se traduit par l'équation 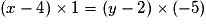 , qui est l'équation de la droite (AB).
, qui est l'équation de la droite (AB).Après transformation de l'égalité, on obtient l'équation :
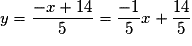 .
.2. Comment utiliser une équation de droite ?
• Pour dire si un point est sur une droite : on remplace les inconnues de l'équation de la droite par les coordonnées du point et on vérifie si l'égalité ainsi obtenue est vraie.
Par exemple, le point E de coordonnées (2 ; −1) est-il sur la droite d'équation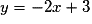 ?
?
Pour répondre, on remplace x par 2 dans la formule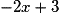 ; si l'on trouve −1 le point est sur la droite, sinon il ne l'est pas.
; si l'on trouve −1 le point est sur la droite, sinon il ne l'est pas.
Ici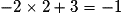 donc le point E est bien sur la droite.
donc le point E est bien sur la droite.
Par exemple, le point E de coordonnées (2 ; −1) est-il sur la droite d'équation
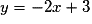 ?
?Pour répondre, on remplace x par 2 dans la formule
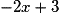 ; si l'on trouve −1 le point est sur la droite, sinon il ne l'est pas.
; si l'on trouve −1 le point est sur la droite, sinon il ne l'est pas.Ici
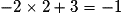 donc le point E est bien sur la droite.
donc le point E est bien sur la droite.• Pour construire une droite, connaissant son équation, on distingue deux cas :
– si l'équation est de la forme x = k, la droite est parallèle à l'axe des ordonnées ; on place le point de coordonnées (k ; 0) et on trace la droite ;
– si l'équation est de la forme y = mx + p, on choisit deux valeurs distinctes x1 et x2 de x et on trace la droite qui passe par les points de coordonnées (x1 ; mx1 + p) et (x2 ; mx2 + p). On peut en particulier choisir x = 0 et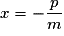 , la droite passe donc par les points (0 ; p) et
, la droite passe donc par les points (0 ; p) et 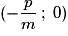 .
.
– si l'équation est de la forme x = k, la droite est parallèle à l'axe des ordonnées ; on place le point de coordonnées (k ; 0) et on trace la droite ;
– si l'équation est de la forme y = mx + p, on choisit deux valeurs distinctes x1 et x2 de x et on trace la droite qui passe par les points de coordonnées (x1 ; mx1 + p) et (x2 ; mx2 + p). On peut en particulier choisir x = 0 et
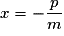 , la droite passe donc par les points (0 ; p) et
, la droite passe donc par les points (0 ; p) et 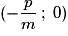 .
.Exemple
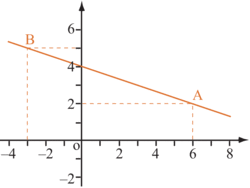
On veut tracer la droite d'équation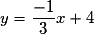 .
.On choisit une valeur de x, par exemple 6 pour pouvoir diviser par 3, puis on calcule :
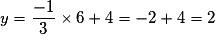 . On obtient le point A de coordonnées (6 ; 2).
. On obtient le point A de coordonnées (6 ; 2).On recommence avec une autre valeur de x, par exemple −3 ; on calcule y et on obtient le point B de coordonnées (-3 ; 5).
Il reste à placer ces points et à tracer la droite.
 |
3. Quels problèmes de géométrie peut-on résoudre à l'aide d'équations de droites ?
• On peut démontrer que deux droites sont parallèles.
Deux droites d'équations respectives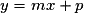 et
et 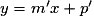 sont parallèles si et seulement si elles ont le même coefficient directeur, c'est-à-dire si
sont parallèles si et seulement si elles ont le même coefficient directeur, c'est-à-dire si 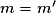 .
.
Par exemple, la droite d'équation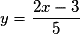 et la droite d'équation
et la droite d'équation 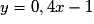 sont parallèles car on peut écrire
sont parallèles car on peut écrire 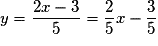 et
et 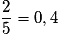 .
.
Deux droites d'équations respectives
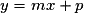 et
et 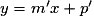 sont parallèles si et seulement si elles ont le même coefficient directeur, c'est-à-dire si
sont parallèles si et seulement si elles ont le même coefficient directeur, c'est-à-dire si 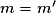 .
.Par exemple, la droite d'équation
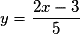 et la droite d'équation
et la droite d'équation 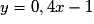 sont parallèles car on peut écrire
sont parallèles car on peut écrire 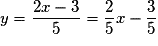 et
et 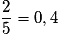 .
.• On peut déterminer l'équation réduite de la parallèle à une droite donnée passant par un point donné.
Par exemple, la parallèle à la droite d'équation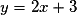 passant par le point A(1 ; 4) a aussi le coefficient directeur 2. Son ordonnée à l'origine b est donnée par :
passant par le point A(1 ; 4) a aussi le coefficient directeur 2. Son ordonnée à l'origine b est donnée par : 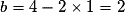 . D'où l'équation cherchée :
. D'où l'équation cherchée : 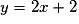 .
.
Exercice n°3
Par exemple, la parallèle à la droite d'équation
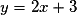 passant par le point A(1 ; 4) a aussi le coefficient directeur 2. Son ordonnée à l'origine b est donnée par :
passant par le point A(1 ; 4) a aussi le coefficient directeur 2. Son ordonnée à l'origine b est donnée par : 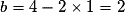 . D'où l'équation cherchée :
. D'où l'équation cherchée : 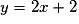 .
.Exercice n°3
4. Comment déterminer un vecteur directeur à partir d'une équation de droite ?
Méthode : Si (D) est une droite passant par le point A et de vecteur directeur 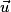 alors pour tout point M de la droite (D), les vecteurs
alors pour tout point M de la droite (D), les vecteurs 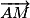 et
et 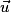 sont colinéaires.
sont colinéaires.
On obtient une équation cartésienne de la forme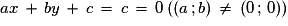 .
.
Remarques : Si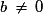 c'est à dire lorsque la droite n'est pas parallèle à l'axe des ordonnées, on peut écrire cette équation sous forme réduite :
c'est à dire lorsque la droite n'est pas parallèle à l'axe des ordonnées, on peut écrire cette équation sous forme réduite : 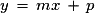 .
.
Une droite a une infinité d'équations cartésiennes, il suffit de multiplier les deux membre de l'égalité par un nombre réel différent de 0. Mais l'équation réduite est unique.
Exemple : Soit la droite (D), passant par le point A(1 ; 2) et de vecteur directeur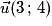 .
.
Si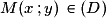 alors
alors 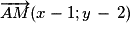 et
et 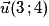 sont colinéaires.
sont colinéaires.
Donc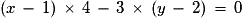 soit
soit 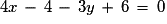 ou
ou 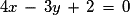 .
.
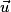 alors pour tout point M de la droite (D), les vecteurs
alors pour tout point M de la droite (D), les vecteurs 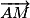 et
et 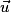 sont colinéaires.
sont colinéaires.On obtient une équation cartésienne de la forme
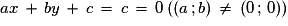 .
.Remarques : Si
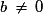 c'est à dire lorsque la droite n'est pas parallèle à l'axe des ordonnées, on peut écrire cette équation sous forme réduite :
c'est à dire lorsque la droite n'est pas parallèle à l'axe des ordonnées, on peut écrire cette équation sous forme réduite : 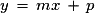 .
.Une droite a une infinité d'équations cartésiennes, il suffit de multiplier les deux membre de l'égalité par un nombre réel différent de 0. Mais l'équation réduite est unique.
Exemple : Soit la droite (D), passant par le point A(1 ; 2) et de vecteur directeur
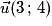 .
.Si
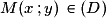 alors
alors 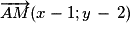 et
et 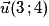 sont colinéaires.
sont colinéaires.Donc
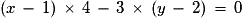 soit
soit 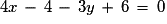 ou
ou 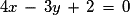 .
.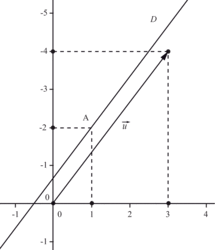 |
Démonstration :
Soit (d) la droite de vecteur directeur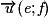 et passant par A(xA ; yA).
et passant par A(xA ; yA).
Soit M(x, y) un point de (d). Alors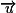 et
et 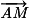 sont colinéaires. Or
sont colinéaires. Or 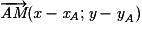 .
.
Donc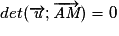 soit e × (y − yA) − f × (x − xA) = 0.
soit e × (y − yA) − f × (x − xA) = 0.
Soit ey − eyA − fx + fxA = 0 ou fx + (−e)y + (fxA − eyA = 0).
On a bien (d) : ax + by + c = 0 avec a, b et c trois réels.
Algorithme : Déterminer une équation cartésienne d'une droite.
Soit (d) la droite de vecteur directeur
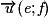 et passant par A(xA ; yA).
et passant par A(xA ; yA).Soit M(x, y) un point de (d). Alors
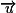 et
et 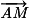 sont colinéaires. Or
sont colinéaires. Or 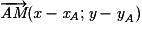 .
.Donc
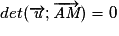 soit e × (y − yA) − f × (x − xA) = 0.
soit e × (y − yA) − f × (x − xA) = 0.Soit ey − eyA − fx + fxA = 0 ou fx + (−e)y + (fxA − eyA = 0).
On a bien (d) : ax + by + c = 0 avec a, b et c trois réels.
Algorithme : Déterminer une équation cartésienne d'une droite.
 |
5. Comment déterminer un vecteur directeur à partir d'une équation de droite ?
Cas d'une équation cartésienne a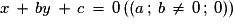 :
:
Le système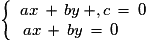 n'a pas de solution pour
n'a pas de solution pour 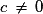 et une infinité de solutions pour
et une infinité de solutions pour 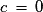 . Les droites d'équations
. Les droites d'équations 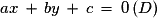 et
et 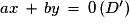 sont donc parallèles et distinctes ou parallèles et confondues.
sont donc parallèles et distinctes ou parallèles et confondues.
Les points O(0 ; 0) et A(− b ; a) appartiennent à la droite (D'), donc le vecteur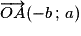 est un vecteur directeur de (D') et de (D).
est un vecteur directeur de (D') et de (D).
Cas d'une équation réduite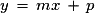 :
:
Le système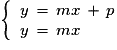 n'a pas de solution pour
n'a pas de solution pour 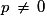 et une infinité de solutions pour
et une infinité de solutions pour 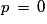 .
.
Les droites d'équations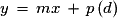 et
et 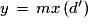 sont donc parallèles et distinctes ou parallèles et confondues.
sont donc parallèles et distinctes ou parallèles et confondues.
Les points O(0 ; 0) et B(1 ; m) appartiennent à la droite (d'), donc le vecteur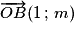 est un vecteur directeur de (d') et de (d).
est un vecteur directeur de (d') et de (d).
Droites parallèles : Deux droites sont parallèles si et seulement si un vecteur directeur de l'une est colinéaire à un vecteur directeur de l'autre.
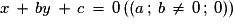 :
:Le système
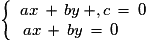 n'a pas de solution pour
n'a pas de solution pour 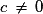 et une infinité de solutions pour
et une infinité de solutions pour 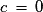 . Les droites d'équations
. Les droites d'équations 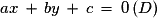 et
et 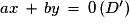 sont donc parallèles et distinctes ou parallèles et confondues.
sont donc parallèles et distinctes ou parallèles et confondues.Les points O(0 ; 0) et A(− b ; a) appartiennent à la droite (D'), donc le vecteur
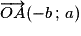 est un vecteur directeur de (D') et de (D).
est un vecteur directeur de (D') et de (D).Cas d'une équation réduite
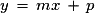 :
:Le système
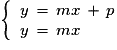 n'a pas de solution pour
n'a pas de solution pour 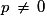 et une infinité de solutions pour
et une infinité de solutions pour 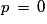 .
.Les droites d'équations
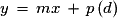 et
et 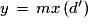 sont donc parallèles et distinctes ou parallèles et confondues.
sont donc parallèles et distinctes ou parallèles et confondues.Les points O(0 ; 0) et B(1 ; m) appartiennent à la droite (d'), donc le vecteur
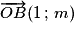 est un vecteur directeur de (d') et de (d).
est un vecteur directeur de (d') et de (d).Droites parallèles : Deux droites sont parallèles si et seulement si un vecteur directeur de l'une est colinéaire à un vecteur directeur de l'autre.
6. Comment décomposer un vecteur en fonction de deux vecteurs non nuls et non colinéaires ?
Base de deux vecteurs : Dans le plan, un point et deux vecteurs non nuls et non colinéaires constituent un repère cartésien. Les deux seuls vecteurs constituent alors une base.
Propriété : Tout vecteur du plan s'écrit de manière unique en fonction des deux vecteurs d'une base.
Si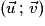 est une base du plan, alors tout vecteur
est une base du plan, alors tout vecteur 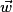 s'écrit de manière unique sous la forme :
s'écrit de manière unique sous la forme :
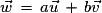 , avec
, avec 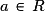 et
et 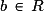 .
.
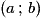 est le couple des coordonnées du vecteur
est le couple des coordonnées du vecteur 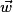 .
.
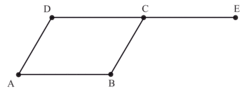
Exemple : Soit un parallélogramme ABCD et E le symétrique de D par rapport à C.
Propriété : Tout vecteur du plan s'écrit de manière unique en fonction des deux vecteurs d'une base.
Si
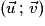 est une base du plan, alors tout vecteur
est une base du plan, alors tout vecteur 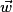 s'écrit de manière unique sous la forme :
s'écrit de manière unique sous la forme :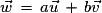 , avec
, avec 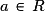 et
et 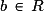 .
.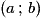 est le couple des coordonnées du vecteur
est le couple des coordonnées du vecteur 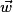 .
.Exemple : Soit un parallélogramme ABCD et E le symétrique de D par rapport à C.
 |
D'après la relation de Chasles :
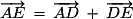 ,
,
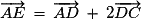 ,
,
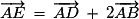 ,
,
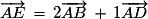 ,
,
Le vecteur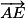 a pour coordonnées
a pour coordonnées 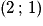 dans la base
dans la base 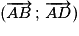 ;
;
le point E a pour coordonnées (2 ; 1) dans le repère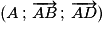 .
.
Exercice n°8Exercice n°9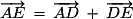 ,
,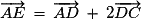 ,
,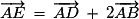 ,
,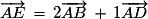 ,
,Le vecteur
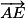 a pour coordonnées
a pour coordonnées 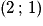 dans la base
dans la base 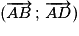 ;
;le point E a pour coordonnées (2 ; 1) dans le repère
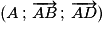 .
.7. Comment déterminer par le calcul le point d'intersection de deux droites ?
• Une équation d'une droite D peut s'écrire sous la forme 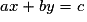 avec a et b non simultanément nuls. Une telle équation s'appelle équation linéaire à deux inconnues. Les solutions de cette équation sont les coordonnées des points de la droite D.
avec a et b non simultanément nuls. Une telle équation s'appelle équation linéaire à deux inconnues. Les solutions de cette équation sont les coordonnées des points de la droite D.
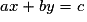 avec a et b non simultanément nuls. Une telle équation s'appelle équation linéaire à deux inconnues. Les solutions de cette équation sont les coordonnées des points de la droite D.
avec a et b non simultanément nuls. Une telle équation s'appelle équation linéaire à deux inconnues. Les solutions de cette équation sont les coordonnées des points de la droite D.• Déterminer par le calcul les coordonnées du point d'intersection de deux droites revient à résoudre un système de deux équations linéaires à deux inconnues constitué des deux équations des deux droites. C'est un système de la forme : 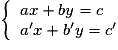 .
.
Résoudre un tel système, c'est trouver tous les couples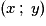 qui sont solutions des deux équations en même temps. Si de tels couples existent, les points qu'ils repèrent appartiennent aux droites d'équations respectives
qui sont solutions des deux équations en même temps. Si de tels couples existent, les points qu'ils repèrent appartiennent aux droites d'équations respectives 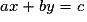 et
et 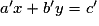 .
.
On distingue trois cas présentés dans le tableau ci-dessous.
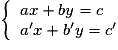 .
.Résoudre un tel système, c'est trouver tous les couples
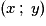 qui sont solutions des deux équations en même temps. Si de tels couples existent, les points qu'ils repèrent appartiennent aux droites d'équations respectives
qui sont solutions des deux équations en même temps. Si de tels couples existent, les points qu'ils repèrent appartiennent aux droites d'équations respectives 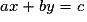 et
et 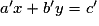 .
.On distingue trois cas présentés dans le tableau ci-dessous.
| Position des droites | Critère algébrique | Solutions |
| Droites sécantes en A(xA ; yA) | 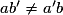 , les coefficients directeurs , les coefficients directeurs 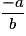 et et 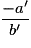 des deux droites sont différents des deux droites sont différents | Une solution unique : le couple (xA ; yA) est solution du système |
| Droites strictement parallèles | 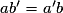 et et 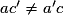 | Pas de solution |
| Droites confondues | 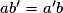 et et 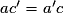 | Tous les couples (x ; y) qui vérifient l'équation 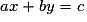 sont solutions, il y en a une infinité sont solutions, il y en a une infinité |
• Il existe deux méthodes pour résoudre algébriquement un système de deux équations linéaires à deux inconnues :
– la méthode par substitution, qui consiste à exprimer une des inconnues en fonction de l'autre dans une équation puis à remplacer cette inconnue par l'expression obtenue dans l'autre équation ;
– la méthode par combinaison, qui consiste à obtenir, en combinant les deux équations, une équation dans laquelle il n'y a plus qu'une inconnue. Cette équation étant résolue, on calcule l'autre inconnue en utilisant la valeur trouvée.
Exercice n°10Exercice n°11
– la méthode par substitution, qui consiste à exprimer une des inconnues en fonction de l'autre dans une équation puis à remplacer cette inconnue par l'expression obtenue dans l'autre équation ;
– la méthode par combinaison, qui consiste à obtenir, en combinant les deux équations, une équation dans laquelle il n'y a plus qu'une inconnue. Cette équation étant résolue, on calcule l'autre inconnue en utilisant la valeur trouvée.
Exercice n°10Exercice n°11
À retenir
• Si une droite est parallèle à l'axe des ordonnées, alors son équation est de la forme 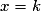 : sinon son équation est de la forme
: sinon son équation est de la forme 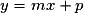 , où m est son coefficient directeur et p son ordonnée à l'origine.
, où m est son coefficient directeur et p son ordonnée à l'origine.
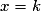 : sinon son équation est de la forme
: sinon son équation est de la forme 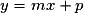 , où m est son coefficient directeur et p son ordonnée à l'origine.
, où m est son coefficient directeur et p son ordonnée à l'origine.• Deux droites sont parallèles si leurs coefficients directeurs sont égaux.
• Deux droites sont perpendiculaires si le produit de leurs coefficients directeurs vaut −1.
• Calculer les coordonnées du point d'intersection de deux droites revient à résoudre le système constitué des deux équations des droites en question.
• Soient 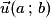 et
et 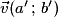 , avec
, avec 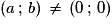 .
.
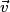 est colinéaire à
est colinéaire à 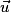 si et seulement si
si et seulement si 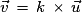 (
(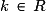 ) ou
) ou 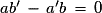 ;
;
Toute droite du plan a une équation de la forme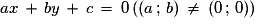 .
.
Si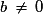 , la droite n'est pas verticale et son équation peut s'écrire
, la droite n'est pas verticale et son équation peut s'écrire 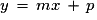 .
.
Un vecteur directeur est de la forme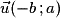 ou
ou 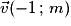 .
.
Si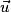 et
et 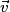 sont deux vecteurs non nuls et non colinéaires du plan, tout vecteur
sont deux vecteurs non nuls et non colinéaires du plan, tout vecteur 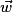 de ce plan se décompose de manière unique sous la forme
de ce plan se décompose de manière unique sous la forme 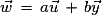 (
(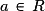 et
et 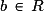 ).
).
(a ; b) est le couple de coordonnées de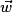 .
.
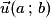 et
et 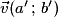 , avec
, avec 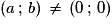 .
.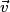 est colinéaire à
est colinéaire à 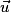 si et seulement si
si et seulement si 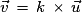 (
(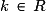 ) ou
) ou 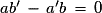 ;
;Toute droite du plan a une équation de la forme
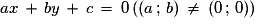 .
.Si
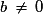 , la droite n'est pas verticale et son équation peut s'écrire
, la droite n'est pas verticale et son équation peut s'écrire 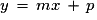 .
.Un vecteur directeur est de la forme
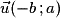 ou
ou 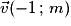 .
.Si
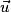 et
et 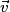 sont deux vecteurs non nuls et non colinéaires du plan, tout vecteur
sont deux vecteurs non nuls et non colinéaires du plan, tout vecteur 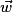 de ce plan se décompose de manière unique sous la forme
de ce plan se décompose de manière unique sous la forme 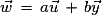 (
(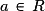 et
et 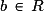 ).
).(a ; b) est le couple de coordonnées de
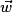 .
.© 2000-2025, Miscellane