Repérage dans le plan et calcul vectoriel
Fiche
En utilisant les nombres réels, on a pu associer à chaque point d'une droite munie d'un repère (O ; I) un nombre appelé son abscisse.
On peut de même associer à chaque point d'un plan muni d'un repère (O ; I, J) deux nombres qui sont les coordonnées du point.
Dans un plan muni d'un repère, on peut calculer les coordonnées d'un vecteur et effectuer différents types de calcul vectoriel pour résoudre des problèmes de géométrie.
On peut de même associer à chaque point d'un plan muni d'un repère (O ; I, J) deux nombres qui sont les coordonnées du point.
Dans un plan muni d'un repère, on peut calculer les coordonnées d'un vecteur et effectuer différents types de calcul vectoriel pour résoudre des problèmes de géométrie.
1. Comment repérer un point dans un plan ?
• On commence par définir un repère du plan : un repère du plan est un triplet de points non alignés (le mot triplet signifie que les trois points considérés sont ordonnés).
En général, on appelle le repère (O ; I, J), où O est l'origine du repère ; la droite (OI) est l'axe des abscisses et la droite (OJ) est l'axe des ordonnées.
En général, on appelle le repère (O ; I, J), où O est l'origine du repère ; la droite (OI) est l'axe des abscisses et la droite (OJ) est l'axe des ordonnées.
• Ensuite, à l'aide du repère, on associe à un point un couple unique de nombres réels en traçant des parallèles aux axes passant par le point.
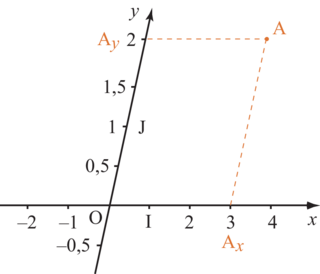 |
Cherchons par exemple les coordonnées de A sur la figure ci-dessus.
On note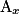 le point d'intersection de (OI) et de la parallèle à (OJ) passant par A et
le point d'intersection de (OI) et de la parallèle à (OJ) passant par A et 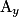 le point d'intersection de (OJ) et de la parallèle à (OI) passant par A.
le point d'intersection de (OJ) et de la parallèle à (OI) passant par A.
On détermine les coordonnées de A en prenant :
– pour l'abscisse de A, l'abscisse du point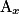 sur la droite graduée (OI) d'origine O,
sur la droite graduée (OI) d'origine O,
– pour l'ordonnée de A, l'abscisse du point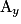 sur la droite graduée (OJ) d'origine O.
sur la droite graduée (OJ) d'origine O.
Ici, les coordonnées du point A sont (3 ; 2).
On note
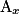 le point d'intersection de (OI) et de la parallèle à (OJ) passant par A et
le point d'intersection de (OI) et de la parallèle à (OJ) passant par A et 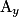 le point d'intersection de (OJ) et de la parallèle à (OI) passant par A.
le point d'intersection de (OJ) et de la parallèle à (OI) passant par A.On détermine les coordonnées de A en prenant :
– pour l'abscisse de A, l'abscisse du point
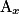 sur la droite graduée (OI) d'origine O,
sur la droite graduée (OI) d'origine O,– pour l'ordonnée de A, l'abscisse du point
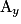 sur la droite graduée (OJ) d'origine O.
sur la droite graduée (OJ) d'origine O.Ici, les coordonnées du point A sont (3 ; 2).
Remarques
Si les axes sont perpendiculaires (O ; I, J) est un repère orthogonal.Si les axes sont perpendiculaires et si de plus OI = OJ, alors (O ; I, J) est un repère orthonormal.
Exercice n°1
2. Comment définir un vecteur ? Comment définir l'égalité de deux vecteurs ?
• Soit un plan dans lequel on a défini une unité de longueur. Un vecteur 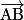 est caractérisé par trois données :
est caractérisé par trois données :
– sa direction : celle de la droite (AB) ;
– son sens : celui de A vers B ;
– sa longueur : la distance AB.
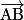 est caractérisé par trois données :
est caractérisé par trois données :– sa direction : celle de la droite (AB) ;
– son sens : celui de A vers B ;
– sa longueur : la distance AB.
• Le vecteur 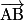 est égal au vecteur
est égal au vecteur 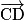 si ces deux vecteurs ont :
si ces deux vecteurs ont :
– la même direction, c'est-à-dire si (AB) // (CD) ;
– le même sens, c'est-à-dire si les points B et D sont du même côté de la droite (AC) ;
– la même longueur, c'est-à-dire si AB = CD.
Autrement dit :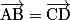 si et seulement si ABDC est un parallélogramme.
si et seulement si ABDC est un parallélogramme.
Ou encore :
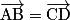 si et seulement si l'image de C par la translation qui transforme A en B est D.
si et seulement si l'image de C par la translation qui transforme A en B est D.
 si et seulement si [AD] et [BC] ont le même milieu ;
si et seulement si [AD] et [BC] ont le même milieu ;
Exercice n°2
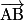 est égal au vecteur
est égal au vecteur 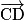 si ces deux vecteurs ont :
si ces deux vecteurs ont :– la même direction, c'est-à-dire si (AB) // (CD) ;
– le même sens, c'est-à-dire si les points B et D sont du même côté de la droite (AC) ;
– la même longueur, c'est-à-dire si AB = CD.
Autrement dit :
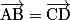 si et seulement si ABDC est un parallélogramme.
si et seulement si ABDC est un parallélogramme.Ou encore :
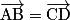 si et seulement si l'image de C par la translation qui transforme A en B est D.
si et seulement si l'image de C par la translation qui transforme A en B est D.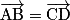 si et seulement si [AD] et [BC] ont le même milieu ;
si et seulement si [AD] et [BC] ont le même milieu ;Exercice n°2
3. Quelles opérations peut-on effectuer sur des vecteurs ?
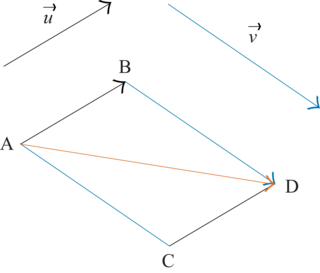
• La somme de deux vecteurs est un vecteur que l'on peut construire de deux façons :
– avec la relation de Chasles en partant d'un point A :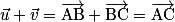 ;
;
– avec la relation de Chasles en partant d'un point A :
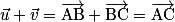 ;
;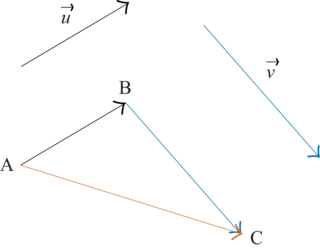 |
– avec la règle du parallélogramme : 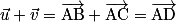 .
.
 .
. |
Remarque
La relation de Chasles sert aussi à décomposer un vecteur en une somme de vecteurs. Si A et B sont deux points donnés, alors, pour tout point C, on a :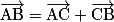 .
.• On définit la multiplication d'un vecteur par un réel de la manière suivante.
Soit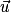 un vecteur non nul et k un nombre réel non nul, le vecteur
un vecteur non nul et k un nombre réel non nul, le vecteur 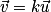 est défini ainsi :
est défini ainsi :
– a la même direction que
a la même direction que  ;
;
–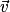 a le même sens que
a le même sens que 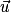 si k est positif, le sens contraire si k est négatif.
si k est positif, le sens contraire si k est négatif.
Si k = −1, alors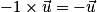 , ce qui définit le vecteur opposé à
, ce qui définit le vecteur opposé à 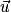 .
.
Soit
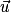 un vecteur non nul et k un nombre réel non nul, le vecteur
un vecteur non nul et k un nombre réel non nul, le vecteur 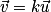 est défini ainsi :
est défini ainsi :–
 a la même direction que
a la même direction que  ;
;–
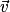 a le même sens que
a le même sens que 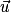 si k est positif, le sens contraire si k est négatif.
si k est positif, le sens contraire si k est négatif.Si k = −1, alors
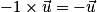 , ce qui définit le vecteur opposé à
, ce qui définit le vecteur opposé à 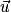 .
.• On appelle vecteurs colinéaires des vecteurs qui ont la même direction. Les vecteurs 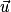 et
et 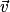 sont colinéaires si et seulement s'il existe un nombre réel k tel que
sont colinéaires si et seulement s'il existe un nombre réel k tel que 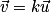 .
.
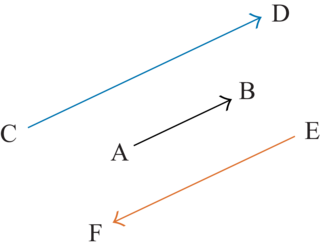
Exemple : sur la figure ci-après, on a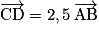 et
et 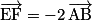 , les vecteurs
, les vecteurs 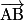 ,
, 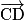 et
et 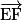 sont colinéaires
sont colinéaires
Exercice n°3Exercice n°4
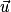 et
et 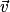 sont colinéaires si et seulement s'il existe un nombre réel k tel que
sont colinéaires si et seulement s'il existe un nombre réel k tel que 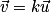 .
.Exemple : sur la figure ci-après, on a
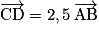 et
et 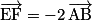 , les vecteurs
, les vecteurs 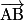 ,
, 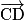 et
et 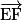 sont colinéaires
sont colinéaires Exercice n°3Exercice n°4
 |
4. Quelles sont les bases du calcul vectoriel ?
• Dans un plan muni d'un repère (O ; I, J), à tout vecteur 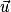 est associé un unique point M tel que
est associé un unique point M tel que  , le point M est l'image de l'origine O du repère par la translation de vecteur
, le point M est l'image de l'origine O du repère par la translation de vecteur  .
.
Par définition, les coordonnées de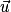 sont celles de M : si M a pour coordonnées
sont celles de M : si M a pour coordonnées 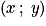 , le vecteur
, le vecteur 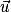 a pour coordonnées
a pour coordonnées 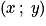 , on écrit
, on écrit 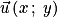 ou aussi
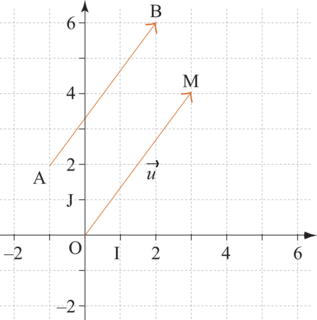
ou aussi 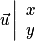 . Par exemple, sur le dessin ci-dessous on a :
. Par exemple, sur le dessin ci-dessous on a : 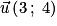 .
.
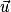 est associé un unique point M tel que
est associé un unique point M tel que 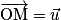 , le point M est l'image de l'origine O du repère par la translation de vecteur
, le point M est l'image de l'origine O du repère par la translation de vecteur 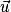 .
.Par définition, les coordonnées de
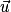 sont celles de M : si M a pour coordonnées
sont celles de M : si M a pour coordonnées 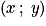 , le vecteur
, le vecteur 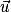 a pour coordonnées
a pour coordonnées 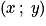 , on écrit
, on écrit 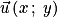 ou aussi
ou aussi 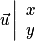 . Par exemple, sur le dessin ci-dessous on a :
. Par exemple, sur le dessin ci-dessous on a : 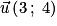 .
. |
Il en découle que deux vecteurs 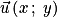 et
et 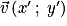 sont égaux si et seulement s'ils ont les mêmes coordonnées :
sont égaux si et seulement s'ils ont les mêmes coordonnées : 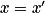 et
et 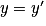 .
.
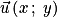 et
et 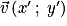 sont égaux si et seulement s'ils ont les mêmes coordonnées :
sont égaux si et seulement s'ils ont les mêmes coordonnées : 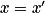 et
et 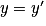 .
.• Il est facile de calculer les coordonnées d'un vecteur 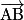 quelconque à partir des coordonnées des points A et B. Dans un repère du plan, soit A un point de coordonnées
quelconque à partir des coordonnées des points A et B. Dans un repère du plan, soit A un point de coordonnées 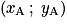 et B un point de coordonnées
et B un point de coordonnées 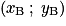 , alors le vecteur
, alors le vecteur 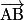 a pour coordonnées
a pour coordonnées 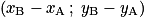 .
.
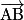 quelconque à partir des coordonnées des points A et B. Dans un repère du plan, soit A un point de coordonnées
quelconque à partir des coordonnées des points A et B. Dans un repère du plan, soit A un point de coordonnées 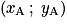 et B un point de coordonnées
et B un point de coordonnées 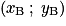 , alors le vecteur
, alors le vecteur 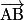 a pour coordonnées
a pour coordonnées 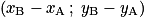 .
.• Soit 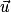 et
et 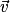 deux vecteurs de coordonnées
deux vecteurs de coordonnées 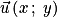 et
et 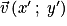 , alors :
, alors :
– la somme de deux vecteurs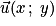 et
et 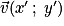 est un vecteur
est un vecteur 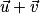 qui a pour coordonnées
qui a pour coordonnées 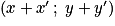 ;
;
– le produit d'un vecteur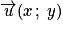 par un réel k est un vecteur
par un réel k est un vecteur 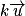 qui a pour coordonnées
qui a pour coordonnées 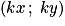 .
.
Exercice n°5Exercice n°6
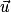 et
et 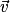 deux vecteurs de coordonnées
deux vecteurs de coordonnées 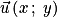 et
et 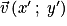 , alors :
, alors :– la somme de deux vecteurs
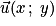 et
et 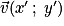 est un vecteur
est un vecteur 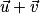 qui a pour coordonnées
qui a pour coordonnées 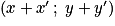 ;
;– le produit d'un vecteur
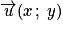 par un réel k est un vecteur
par un réel k est un vecteur 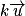 qui a pour coordonnées
qui a pour coordonnées 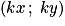 .
.Exercice n°5Exercice n°6
5. Déterminant de deux vecteurs
Définition : Soit 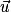 et
et 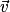 deux vecteurs du plan.
deux vecteurs du plan.
On dit que les vecteurs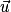 et
et 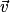 sont une base du plan si et seulement si
sont une base du plan si et seulement si  et
et  ne sont pas colinéaires.
ne sont pas colinéaires.
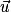 et
et 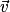 deux vecteurs du plan.
deux vecteurs du plan.On dit que les vecteurs
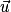 et
et 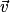 sont une base du plan si et seulement si
sont une base du plan si et seulement si 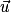 et
et 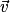 ne sont pas colinéaires.
ne sont pas colinéaires.Définition : Soit 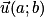 et
et 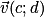 deux vecteurs du plan.
deux vecteurs du plan.
Le déterminant des vecteurs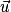 et
et 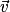 est le réel a × d − b × c. On le note
est le réel a × d − b × c. On le note 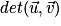 .
.
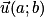 et
et 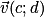 deux vecteurs du plan.
deux vecteurs du plan.Le déterminant des vecteurs
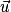 et
et 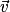 est le réel a × d − b × c. On le note
est le réel a × d − b × c. On le note 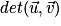 .
.Propriété : Soit 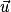 et
et 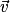 deux vecteurs du plan.
deux vecteurs du plan.
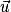 et
et 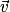 sont colinéaires si et seulement si
sont colinéaires si et seulement si 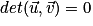 .
.
 et
et  deux vecteurs du plan.
deux vecteurs du plan. et
et 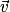 sont colinéaires si et seulement si
sont colinéaires si et seulement si 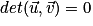 .
.Démonstration : 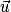 et
et 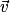 sont colinéaires si et seulement si
sont colinéaires si et seulement si 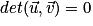 .
.
Soit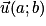 et
et 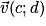 deux vecteurs du plan.
deux vecteurs du plan.
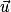 et
et 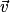 sont colinéaires si et seulement si :
sont colinéaires si et seulement si :
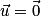 alors
alors 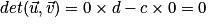 .
.
Ou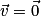 alors
alors 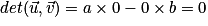 .
.
Ou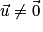 et
et 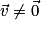 alors il existe un réel k tel que
alors il existe un réel k tel que 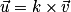 .
.
Si a = 0 alors c = 0 et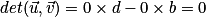 .
.
Si b = 0 alors d = 0 et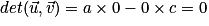 .
.
Si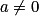 et
et 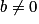 alors
alors 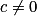 et
et 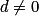 et a = k ×c et b = k ×d.
et a = k ×c et b = k ×d.
Donc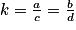 ainsi ad = bc d'où ad − bc = 0 donc
ainsi ad = bc d'où ad − bc = 0 donc 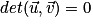 .
.
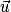 et
et 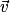 sont colinéaires si et seulement si
sont colinéaires si et seulement si 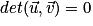 .
.Soit
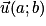 et
et 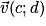 deux vecteurs du plan.
deux vecteurs du plan.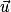 et
et 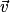 sont colinéaires si et seulement si :
sont colinéaires si et seulement si :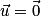 alors
alors 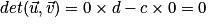 .
.Ou
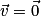 alors
alors 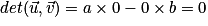 .
.Ou
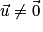 et
et 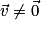 alors il existe un réel k tel que
alors il existe un réel k tel que 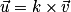 .
.Si a = 0 alors c = 0 et
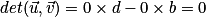 .
.Si b = 0 alors d = 0 et
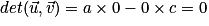 .
.Si
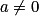 et
et 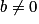 alors
alors 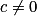 et
et 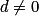 et a = k ×c et b = k ×d.
et a = k ×c et b = k ×d.Donc
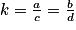 ainsi ad = bc d'où ad − bc = 0 donc
ainsi ad = bc d'où ad − bc = 0 donc 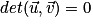 .
.Propriété 1 : A, B et C sont alignés si et seulement si 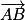 et
et 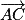 sont colinéaires.
sont colinéaires.
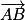 et
et 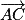 sont colinéaires.
sont colinéaires.Propriété 2 : (AB) et (CD) sont paralléles si et seulement si 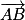 et
et 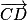 sont colinéaires.
sont colinéaires.
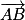 et
et 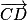 sont colinéaires.
sont colinéaires.Algorithme : Déterminer si trois points sont alignés.
 |
Par exemple, les vecteurs 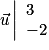 et
et 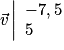 sont colinéaires car : det (
sont colinéaires car : det (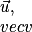 ) =
) = 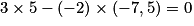 .
.
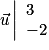 et
et 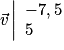 sont colinéaires car : det (
sont colinéaires car : det (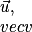 ) =
) = 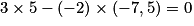 .
.6. Deux propriétés fondamentales
Propriété 1 : Soit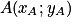 et
et 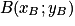 deux points du plan.
deux points du plan.Le milieu du segment [AB] est le point M dont les coordonnées sont
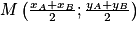 .
.Propriété 2 : Si A et B sont deux points de coordonnées respectives
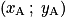 et
et 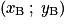 , alors on a tout naturellement :
, alors on a tout naturellement :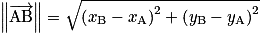 .
.Exercice n°8
À retenir
• Un repère du plan est un triplet de points non alignés. À chaque point du plan, on associe un couple unique de nombres réels, ses coordonnées, en traçant des parallèles aux axes passant par ce point.
• Dans un plan muni d'une unité de longueur, un vecteur 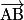 est caractérisé par trois données : sa direction, son sens et sa longueur.
est caractérisé par trois données : sa direction, son sens et sa longueur.
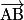 est caractérisé par trois données : sa direction, son sens et sa longueur.
est caractérisé par trois données : sa direction, son sens et sa longueur.• La somme de deux vecteurs 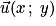 et
et 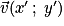 est un vecteur
est un vecteur 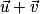 qui a pour coordonnées
qui a pour coordonnées 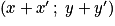 . Le produit d'un vecteur
. Le produit d'un vecteur 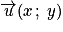 par un réel k est un vecteur
par un réel k est un vecteur 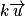 qui a pour coordonnées
qui a pour coordonnées 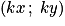 .
.
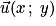 et
et 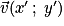 est un vecteur
est un vecteur 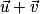 qui a pour coordonnées
qui a pour coordonnées 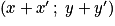 . Le produit d'un vecteur
. Le produit d'un vecteur 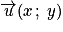 par un réel k est un vecteur
par un réel k est un vecteur 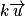 qui a pour coordonnées
qui a pour coordonnées 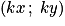 .
.• Les vecteurs 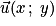 et
et 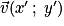 sont colinéaires si et seulement si
sont colinéaires si et seulement si 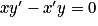 .
.
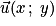 et
et 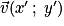 sont colinéaires si et seulement si
sont colinéaires si et seulement si 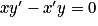 .
.7. Projeté orthogonal
Définition : Soit un point M est un point extérieur à une droite (d). On dit que le point N de la droite (d) est le projeté orthogonal du point M sur la droite (d) lorsque les droites (MN) et (d) sont perpendiculaires.Démonstration : Le projeté de M sur (d) est le point le plus proche de M.
Soit un point M est un point extérieur à une droite (d). Soit H le projeté orthogonal de M sur (d).
Soit A un point de la droite (d) distinct de H. Le triangle MHA est rectangle en H donc d'après le théorème de Pythagore on a l'géalité suivante : MA2 + HA2 + MH2 . Or A et H distinct donc HA > 0 donc HA2 > 0.
Donc MA2 > MH2. Or la fonction racine carrée est croissante sur
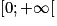 donc
donc 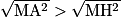 .
.Comme MA > 0 et MH > 0 alors MA > MH.
Ainsi H est bien le point de (d) le plus proche de M.
Exercice n°9
© 2000-2026, Miscellane