Équations et inéquations
Fiche
Pour résoudre une équation ou une inéquation du premier degré à une inconnue, on isole le terme inconnu dans un membre. De nouveaux types d'équations et inéquations apparaissent, comportant l'inconnue au carré ou au dénominateur. On s'intéresse également à la résolution conjointe de deux équations (ou de deux inéquations). Cette situation se retrouve par exemple lorsque l'on cherche à déterminer les coordonnées du point d'intersection de deux droites.
1. Quelles sont les méthodes pour résoudre une équation ou une inéquation comportant des carrés ?
• Pour résoudre une équation comportant des carrés, on revient à une écriture de la forme 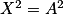 . Deux nombres opposés ont le même carré, donc :
. Deux nombres opposés ont le même carré, donc :
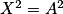 équivaut à
équivaut à 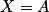 ou
ou 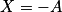 .
.
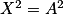 . Deux nombres opposés ont le même carré, donc :
. Deux nombres opposés ont le même carré, donc :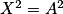 équivaut à
équivaut à 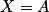 ou
ou 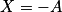 .
.Exemple
Résoudre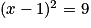 revient à écrire : x −1 = 3 ou x −1 = −3,
revient à écrire : x −1 = 3 ou x −1 = −3,soit x = 4 ou x = −2, d'où S = {−2 ; 4}.
• Pour résoudre une inéquation comportant des carrés, on transpose tous les termes dans un seul membre et on factorise, si possible, en un produit de facteurs du premier degré.
On peut alors en déduire l'ensemble des solutions à l'aide d'un tableau de signes.
On peut alors en déduire l'ensemble des solutions à l'aide d'un tableau de signes.
Exemple
Résoudre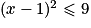 revient à écrire :
revient à écrire : 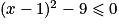 .
.On reconnaît alors la différence de deux carrés :
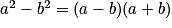 .
.D'où :
![[(x-1)-3][(x -1) + 3] \le {0}](https://static1.assistancescolaire.com/2/images/2_m207_m9.png) , ou encore :
, ou encore : 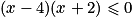 .
.On conclut à l'aide d'un tableau de signes :
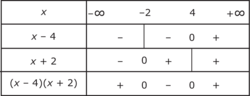 |
Le produit est négatif sur l'intervalle [ - 2 ; 4], d'où : S = [- 2 ; 4].
Exercice n°1
Exercice n°1
2. Quelles sont les méthodes pour résoudre une équation ou une inéquation comportant l'inconnue au dénominateur ?
• Dans le cas d'une équation, on écrit l'égalité des « produits en croix » pour obtenir une égalité sans dénominateur.
Exemple
Pour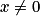 , résoudre l'équation
, résoudre l'équation 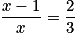 équivaut à résoudre :
équivaut à résoudre : 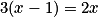 .
.D'où :
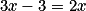 , ou encore
, ou encore 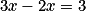 , soit x = 3.
, soit x = 3.L'ensemble des solutions es S = {3}.
• Dans le cas d'une inéquation, on transpose tous les termes dans un seul membre et on fait apparaître si possible un quotient de facteurs du premier degré. On peut alors déterminer l'ensemble des solutions à l'aide d'un tableau de signes.
Exemple
Pour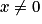 , résoudre l'équation
, résoudre l'équation 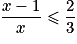 équivaut à résoudre
équivaut à résoudre 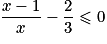 .
.En réduisant au même dénominateur, on obtient :
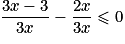 , soit
, soit 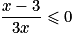 .
.On conclut à l'aide d'un tableau de signes :
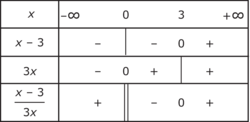 |
Le quotient est négatif sur l'intervalle ]0 ; 3], donc ![S = \:]0 ; 3]](https://static1.assistancescolaire.com/2/images/2_m207_m21.png) .
.
![S = \:]0 ; 3]](https://static1.assistancescolaire.com/2/images/2_m207_m21.png) .
.3. Comment résoudre un système d'équations du premier degré à deux inconnues ?
Il y a deux méthodes : par substitution ou par addition.• Si l'une des inconnues possède un coefficient égal à 1 ou −1, il est préférable d'utiliser la méthode par substitution.
Dans l'une des équations, on écrit l'inconnue dont le coefficient est 1 ou −1 en fonction de l'autre, puis on substitue cette écriture à l'inconnue de la seconde équation.
Dans l'une des équations, on écrit l'inconnue dont le coefficient est 1 ou −1 en fonction de l'autre, puis on substitue cette écriture à l'inconnue de la seconde équation.
Exemple
Dans le système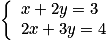 , on exprime x en fonction de y dans la première équation et on obtient le système équivalent :
, on exprime x en fonction de y dans la première équation et on obtient le système équivalent : 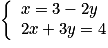 .
.On remplace ensuite x par
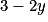 dans la seconde équation, ce qui donne le système :
dans la seconde équation, ce qui donne le système :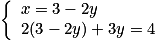 qui équivaut à
qui équivaut à 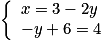 , soit encore à
, soit encore à 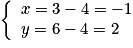 .
.On obtient ainsi le couple solution :
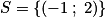 .
.• Si les coefficients des inconnues sont différents de 1 ou de −1, pour éviter l'apparition d'écritures fractionnaires, on utilise la méthode par addition.
Cette méthode consiste à faire apparaître des coefficients opposés pour l'une des inconnues, en multipliant les équations par des réels bien choisis. En additionnant membre à membre les deux équations transformées, on obtient une équation à une seule inconnue que l'on peut résoudre. On utilise alors ce résultat pour résoudre l'autre équation.
Cette méthode consiste à faire apparaître des coefficients opposés pour l'une des inconnues, en multipliant les équations par des réels bien choisis. En additionnant membre à membre les deux équations transformées, on obtient une équation à une seule inconnue que l'on peut résoudre. On utilise alors ce résultat pour résoudre l'autre équation.
Exemple
Dans le système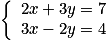 , on multiplie les termes de la première équation par 2 et ceux de la seconde par 3 et on obtient le système équivalent :
, on multiplie les termes de la première équation par 2 et ceux de la seconde par 3 et on obtient le système équivalent : 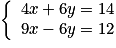 .
.On additionne membre à membre les deux équations et on remplace la seconde équation du système par le résultat ; on obtient le système équivalent :
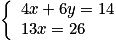 , soit encore
, soit encore 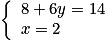 ou
ou 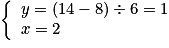 .
.On en déduit le couple solution :
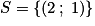 .
.• Un système peut n'avoir aucune solution ou encore une infinité de solutions.
Soit le système :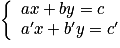 . Si les coefficients de x et de y sont proportionnels, c'est-à-dire si
. Si les coefficients de x et de y sont proportionnels, c'est-à-dire si 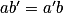 , ce système a une infinité de solutions ou pas de solution du tout :
, ce système a une infinité de solutions ou pas de solution du tout :
– si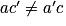 , alors le sysème n'a pas de solution ;
, alors le sysème n'a pas de solution ;
– si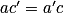 (les coefficients des deux équations sont proportionnels), alors le système a une infinité de solutions.
(les coefficients des deux équations sont proportionnels), alors le système a une infinité de solutions.
Exercice n°4
Soit le système :
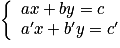 . Si les coefficients de x et de y sont proportionnels, c'est-à-dire si
. Si les coefficients de x et de y sont proportionnels, c'est-à-dire si 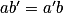 , ce système a une infinité de solutions ou pas de solution du tout :
, ce système a une infinité de solutions ou pas de solution du tout :– si
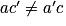 , alors le sysème n'a pas de solution ;
, alors le sysème n'a pas de solution ;– si
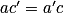 (les coefficients des deux équations sont proportionnels), alors le système a une infinité de solutions.
(les coefficients des deux équations sont proportionnels), alors le système a une infinité de solutions.Exercice n°4
• On trouvera dans la fiche « Lire ou compléter un algorithme », un algorithme permettant de résoudre tout système de deux équations du premier degré à deux inconnues.
4. Comment résoudre un système d'inéquations du premier degré à une inconnue ?
Pour résoudre un système de deux inéquations du premier degré à une inconnue, on résout chacune des inéquations, on obtient ainsi deux intervalles de solutions. On cherche ensuite la partie commune aux deux intervalles ; si elle existe, c'est la solution du système.
Exemple
On veut résoudre le système :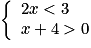 .
.Ce système est équivalent à :
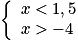 .
.L'ensemble des solutions du système est donc l'intersection de deux intervalles :
![S = ] - \infty\,;\; 1,5[ \: \cap \: ] - 4\,;\; + \infty [](https://static1.assistancescolaire.com/2/images/2_m207_m41.png) . D'où :
. D'où : ![S = ] - 4\,;\; 1,5[](https://static1.assistancescolaire.com/2/images/2_m207_m42.png) . (Il peut être utile de dessiner les intervalles pour déterminer l'intersection.)
. (Il peut être utile de dessiner les intervalles pour déterminer l'intersection.)Exercice n°5
5. Démonstrations
 |
Démonstration 1 : Pour tout réels positifs a et b, 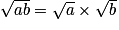
Pour tout réels positifs a et b :
d'une part :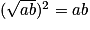 .
.
d'autre part :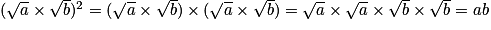 .
.
On a donc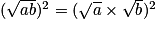 et
et 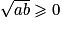 et
et 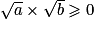 .
.
Ainsi, pour tout réels positifs a et,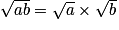 .
.
Démonstration 2 : Pour tout réels strictement positifs a et b,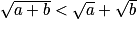
Pour tout réels strictement positifs a et b :
d'une part :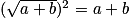 .
.
d'autre part :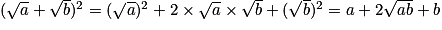
On a donc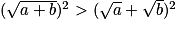 car
car 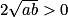
On a donc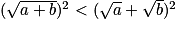 et
et 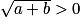 et
et 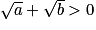 .
.
Donc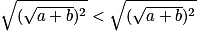 car la fonction racine carrée est croissante sur
car la fonction racine carrée est croissante sur 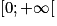 .
.
Ainsi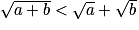 .
.
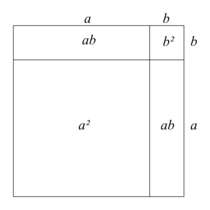
Démonstration 3 : Pour tout réels et positifs, (a + b)2 = a2 + 2ab + b2 .
On considère un grand carré de côté longueur a + b.
On peut construire à l'intérieur de ce carré deux rectangles d'aire ab ainsi que un carré d'aire a2 et un carré d'aire b2.
D'une part le grand carré a pour aire (a + b)2.
D'autre part le grand carré a pour aire ab + b2 + a2 + ab soit a2 + 2ab + b2.
L'aire d'un carré étant unique on a donc (a + b)2 = a2 + 2ab + b2.
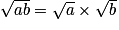
Pour tout réels positifs a et b :
d'une part :
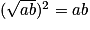 .
.d'autre part :
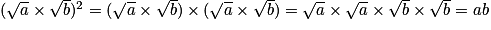 .
.On a donc
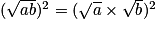 et
et 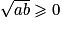 et
et 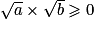 .
.Ainsi, pour tout réels positifs a et,
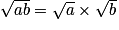 .
.Démonstration 2 : Pour tout réels strictement positifs a et b,
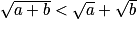
Pour tout réels strictement positifs a et b :
d'une part :
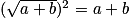 .
.d'autre part :
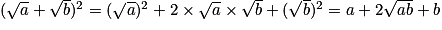
On a donc
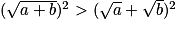 car
car 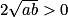
On a donc
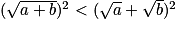 et
et 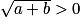 et
et 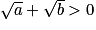 .
.Donc
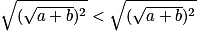 car la fonction racine carrée est croissante sur
car la fonction racine carrée est croissante sur 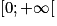 .
.Ainsi
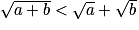 .
.Démonstration 3 : Pour tout réels et positifs, (a + b)2 = a2 + 2ab + b2 .
On considère un grand carré de côté longueur a + b.
On peut construire à l'intérieur de ce carré deux rectangles d'aire ab ainsi que un carré d'aire a2 et un carré d'aire b2.
D'une part le grand carré a pour aire (a + b)2.
D'autre part le grand carré a pour aire ab + b2 + a2 + ab soit a2 + 2ab + b2.
L'aire d'un carré étant unique on a donc (a + b)2 = a2 + 2ab + b2.
 |
Algorithme : Soit a et c deux réels strictement positifs. Déterminer le plus petit entier b tel que 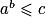 .
.
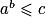 .
.© 2000-2025, Miscellane