Premières fonctions de référence
Fiche
Les fonctions linéaires, qui traduisent la proportionnalité des grandeurs, et les fonctions affines, qui traduisent la proportionnalité des accroissements de ces grandeurs, sont connues depuis le collège. On découvre ici la fonction carré et la fonction inverse, la fonction racine carrée et la fonction cube.
Deux nombres sont-ils toujours dans le même ordre que leurs carrés ? Dans le même ordre que leurs inverses ? L'étude de la fonction carré et de la fonction inverse permet de connaître sur quel intervalle l'ordre est conservé et sur quel intervalle l'ordre est inversé.
En composant ces fonctions de base, on peut en construire beaucoup d'autres.
Deux nombres sont-ils toujours dans le même ordre que leurs carrés ? Dans le même ordre que leurs inverses ? L'étude de la fonction carré et de la fonction inverse permet de connaître sur quel intervalle l'ordre est conservé et sur quel intervalle l'ordre est inversé.
En composant ces fonctions de base, on peut en construire beaucoup d'autres.
1. Quelles sont les caractéristiques de la fonction carré ?
• La fonction carré 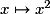 est définie sur
est définie sur  .
.
Elle est décroissante sur![]- \infty\,;\; 0]](https://static1.assistancescolaire.com/2/images/2_m205_m2.png) et croissante sur
et croissante sur 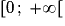 .
.
D'où son tableau de variation :
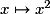 est définie sur
est définie sur  .
.Elle est décroissante sur
![]- \infty\,;\; 0]](https://static1.assistancescolaire.com/2/images/2_m205_m2.png) et croissante sur
et croissante sur 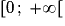 .
.D'où son tableau de variation :
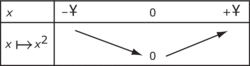 |
• On dresse un tableau de valeurs :
| x | -3 | -2 | -1 | -0,5 | 0 | 0,5 | 1 | 2 | 3 |
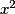 | 9 | 4 | 1 | 0,25 | 0 | 0,25 | 1 | 4 | 9 |
Puis on trace la parabole ci-dessous qui représente la fonction :
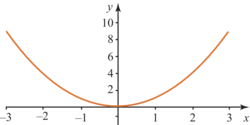 |
Remarque
Deux nombres opposés ont la même image, donc la courbe est symétrique par rapport à l'axe des ordonnées.
Exercice n°1
Exercice n°1
Démonstration :
Démontrons que la fonction carré est strictement croissante sur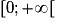 .
.
Soient a et b deux réels de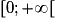 tels que a < b. On veut prouver que a2 < b2 c'est à dire que a2 − b2 < 0 ou encore que (a − b)(a + b) < 0.
tels que a < b. On veut prouver que a2 < b2 c'est à dire que a2 − b2 < 0 ou encore que (a − b)(a + b) < 0.
Or a + b est un réel strictement positif car a et b sont deux réels de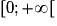 tels que a < b.
tels que a < b.
Et comme a < b alors a − b < 0.
Donc le produit (a − b)(a + b) est un nombre réel strictement négatif.
Ainsi on a bien (a − b)(a + b) < 0 donc a2 − b2 < 0 donc a2 < b2.
Donc la fonction carré est croissante sur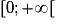 .
.
On procéde de manière similaire pour démontrer que la fonction carré est strictement décroissante sur![]-\infty ;0]](https://static1.assistancescolaire.com/2/images/2_m205_m9.png) .
.
Démontrons que la fonction carré est strictement croissante sur
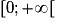 .
.Soient a et b deux réels de
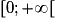 tels que a < b. On veut prouver que a2 < b2 c'est à dire que a2 − b2 < 0 ou encore que (a − b)(a + b) < 0.
tels que a < b. On veut prouver que a2 < b2 c'est à dire que a2 − b2 < 0 ou encore que (a − b)(a + b) < 0.Or a + b est un réel strictement positif car a et b sont deux réels de
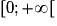 tels que a < b.
tels que a < b.Et comme a < b alors a − b < 0.
Donc le produit (a − b)(a + b) est un nombre réel strictement négatif.
Ainsi on a bien (a − b)(a + b) < 0 donc a2 − b2 < 0 donc a2 < b2.
Donc la fonction carré est croissante sur
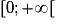 .
.On procéde de manière similaire pour démontrer que la fonction carré est strictement décroissante sur
![]-\infty ;0]](https://static1.assistancescolaire.com/2/images/2_m205_m9.png) .
.2. Quelles sont les caractéristiques de la fonction inverse ?
• La fonction inverse 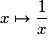 n'est par définie pour x = 0 : elle est définie sur
n'est par définie pour x = 0 : elle est définie sur  .
.
Elles est décroissante sur![]- \infty\,;\; 0[](https://static1.assistancescolaire.com/2/images/2_m205_m11.png) et sur sur
et sur sur ![]0\,;\; + \infty [](https://static1.assistancescolaire.com/2/images/2_m205_m12.png) .
.
D'où son tableau de variation :
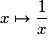 n'est par définie pour x = 0 : elle est définie sur
n'est par définie pour x = 0 : elle est définie sur  .
.Elles est décroissante sur
![]- \infty\,;\; 0[](https://static1.assistancescolaire.com/2/images/2_m205_m11.png) et sur sur
et sur sur ![]0\,;\; + \infty [](https://static1.assistancescolaire.com/2/images/2_m205_m12.png) .
.D'où son tableau de variation :
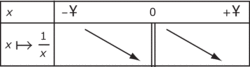 |
• On dresse un tableau de valeurs :
| X | −4 | −2 | −1 | −0,5 | −0,25 | 0 | 0,25 | 0,5 | 1 | 2 | 4 |
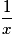 | 0,25 | 0,5 | 1 | 2 | −4 | 0 | 4 | 2 | 1 | 0,5 | 0,25 |
Puis on trace les deux branches de l'hyperbole qui représentent la fonction :
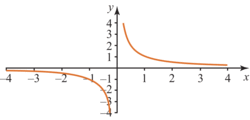 |
Remarque
Deux nombres opposés ont des images opposées, donc la courbe est symétrique par rapport à l'origine.
Exercice n°2
Exercice n°2
Démontrons que la fonction inverse est strictement décroissante sur ![]0;+\infty [](https://static1.assistancescolaire.com/2/images/2_m205_m14.png) .
.
Soient a et b deux réels de![]0;+\infty [](https://static1.assistancescolaire.com/2/images/2_m205_m15.png) tels que a < b. On veut prouver que
tels que a < b. On veut prouver que 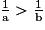 c'est à dire que
c'est à dire que 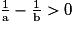
Ou encore que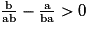 soit
soit 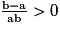 .
.
Or comme a < b alors b − a > 0.
Et comme a et b sont deux réels de![]0;+\infty [](https://static1.assistancescolaire.com/2/images/2_m205_m20.png) alors le produit ab est strictement positif.
alors le produit ab est strictement positif.
Ainsi le quotient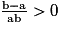 est bien strictement positif.
est bien strictement positif.
Donc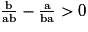 donc
donc 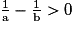 donc
donc 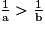 .
.
Ainsi la fonction inverse est strictement décroissante sur![]0;+\infty [](https://static1.assistancescolaire.com/2/images/2_m205_m25.png) .
.
![]0;+\infty [](https://static1.assistancescolaire.com/2/images/2_m205_m14.png) .
.Soient a et b deux réels de
![]0;+\infty [](https://static1.assistancescolaire.com/2/images/2_m205_m15.png) tels que a < b. On veut prouver que
tels que a < b. On veut prouver que 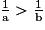 c'est à dire que
c'est à dire que 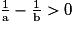
Ou encore que
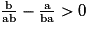 soit
soit 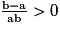 .
.Or comme a < b alors b − a > 0.
Et comme a et b sont deux réels de
![]0;+\infty [](https://static1.assistancescolaire.com/2/images/2_m205_m20.png) alors le produit ab est strictement positif.
alors le produit ab est strictement positif.Ainsi le quotient
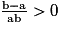 est bien strictement positif.
est bien strictement positif.Donc
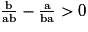 donc
donc 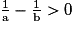 donc
donc 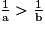 .
.Ainsi la fonction inverse est strictement décroissante sur
![]0;+\infty [](https://static1.assistancescolaire.com/2/images/2_m205_m25.png) .
.3. Quelles sont les caractéristiques de la fonction racine carrée ?
Ensemble de définition : La fonction racine carrée x 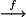
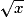 est définie sur l'intervalle
est définie sur l'intervalle 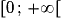 .
.
Sens de variation :
On a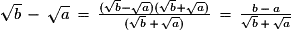
Donc, si 0 a < b alors
a < b alors 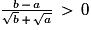 , d'où f(a) < f(b).
, d'où f(a) < f(b).
La fonction racine carrée conserve l'ordre, elle est strictement monotone, strictement croissante.
Représentation graphique :
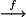
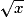 est définie sur l'intervalle
est définie sur l'intervalle 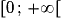 .
.Sens de variation :
On a
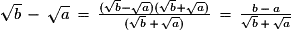
Donc, si 0
 a < b alors
a < b alors 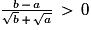 , d'où f(a) < f(b).
, d'où f(a) < f(b).La fonction racine carrée conserve l'ordre, elle est strictement monotone, strictement croissante.
Représentation graphique :
| x | 0 | 0,5 | 1 | 2 |
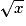 | 0 | 0,707 … | 1 | 1,414 … |
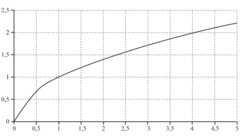 |
4. Quelles sont les caractéristiques de la fonction cube ?
Ensemble de définition : La fonction 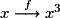 cube est définie sur
cube est définie sur ![D\,=\,]-\infty;\,+\infty[](https://static1.assistancescolaire.com/2/images/2_m205_m33.png) .
.
Sens de variation :
On a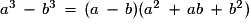 , donc si
, donc si 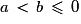 ou si
ou si 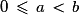 le premier facteur du second terme de l'égalité est négatif et le second est positif, soit
le premier facteur du second terme de l'égalité est négatif et le second est positif, soit 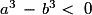 , soit f(a) < f(b).
, soit f(a) < f(b).
La fonction cube ne change pas l'ordre sur les intervalles![]-\infty\,; 0]](https://static1.assistancescolaire.com/2/images/2_m205_m38.png) et
et 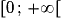 , elle est donc strictement croissante sur l'intervalle
, elle est donc strictement croissante sur l'intervalle ![]\infty\,;\,+\infty[](https://static1.assistancescolaire.com/2/images/2_m205_m40.png) .
.
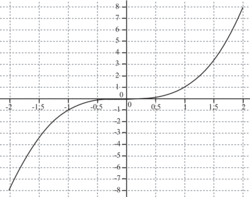
Représentation graphique :
Pour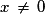 , on a f(−x) = −f(x). La cubique représentant la fonction cube est donc symétrique par rapport à l'origine du repère.
, on a f(−x) = −f(x). La cubique représentant la fonction cube est donc symétrique par rapport à l'origine du repère.
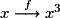 cube est définie sur
cube est définie sur ![D\,=\,]-\infty;\,+\infty[](https://static1.assistancescolaire.com/2/images/2_m205_m33.png) .
.Sens de variation :
On a
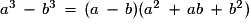 , donc si
, donc si 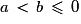 ou si
ou si 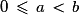 le premier facteur du second terme de l'égalité est négatif et le second est positif, soit
le premier facteur du second terme de l'égalité est négatif et le second est positif, soit 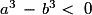 , soit f(a) < f(b).
, soit f(a) < f(b).La fonction cube ne change pas l'ordre sur les intervalles
![]-\infty\,; 0]](https://static1.assistancescolaire.com/2/images/2_m205_m38.png) et
et 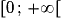 , elle est donc strictement croissante sur l'intervalle
, elle est donc strictement croissante sur l'intervalle ![]\infty\,;\,+\infty[](https://static1.assistancescolaire.com/2/images/2_m205_m40.png) .
.Représentation graphique :
Pour
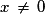 , on a f(−x) = −f(x). La cubique représentant la fonction cube est donc symétrique par rapport à l'origine du repère.
, on a f(−x) = −f(x). La cubique représentant la fonction cube est donc symétrique par rapport à l'origine du repère.| x | 0 | 0,5 | 1 | 1,5 | 2 |
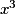 | 0 | 0,125 … | 1 | 3,375 | 8 |
 |
5. Comment comparer un nombre positif, son carré, son cube et sa racine carrée ?
On utilise la représentation graphique sur 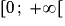 des quatre fonctions :
des quatre fonctions : 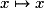 ;
; 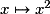 ;
; 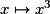 et
et 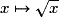 . On obtient le dessin suivant :
. On obtient le dessin suivant :
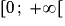 des quatre fonctions :
des quatre fonctions : 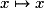 ;
; 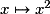 ;
; 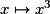 et
et 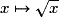 . On obtient le dessin suivant :
. On obtient le dessin suivant :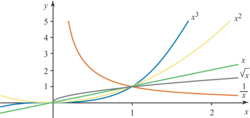 |
Sur ce graphique on peut vérifier les encadrements suivants :
si 0 < x < 1, alors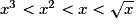 ;
;
si x > 1, alors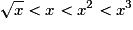 .
.
Exercice n°5
si 0 < x < 1, alors
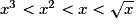 ;
;si x > 1, alors
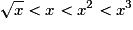 .
.Exercice n°5
Démonstration :
Soit f la fonction identité, g la fonction carré et h la fonction cube.
Etudions le signe de h(x) − g(x) = x3 −x2 = x2(x − 1)
Soit f la fonction identité, g la fonction carré et h la fonction cube.
Etudions le signe de h(x) − g(x) = x3 −x2 = x2(x − 1)
| x | 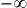 | 0 | 1 | 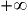 | |||
| x2 | | + | | + | | + | |
| x − 1 | | − | | − | | + | |
| h(x) − g(x) | | − | | − | | + | |
Étudions le signe de g(x) − f(x) = x2 − x = x(x − 1)
Ainsi, pour tout x de [0 ;1], h(x) − g(x) 0 et g(x) − f(x)
0 et g(x) − f(x)  0
0
Et pour tout x de [1 ;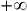 , h(x) − g(x)
, h(x) − g(x) 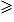 0 et g(x) − f(x)
0 et g(x) − f(x) 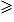 0
0
Donc pour tout x de [0 ;1], h(x) g(x) et g(x)
g(x) et g(x)  f(x) soit h(x)
f(x) soit h(x)  g(x)
g(x)  f(x)
f(x)
Et pour tout x de [1 ;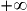 [, h(x)
[, h(x) 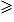 g(x) et g(x)
g(x) et g(x) 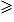 f(x) soit h(x)
f(x) soit h(x) 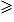 g(x)
g(x) 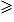 f(x)
f(x)
Ainsi pour tout x de [0 ;1], x3 x2
x2  x et pour tout x de [1 ;
x et pour tout x de [1 ; 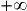 , x
, x  x2
x2  x3.
x3.
| x | 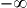 | 0 | 1 | 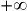 | |||
| x | | − | | + | | + | |
| x − 1 | | − | | − | | + | |
| g(x) − f(x) | | + | | − | | + | |
Ainsi, pour tout x de [0 ;1], h(x) − g(x)
 0 et g(x) − f(x)
0 et g(x) − f(x)  0
0Et pour tout x de [1 ;
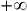 , h(x) − g(x)
, h(x) − g(x) 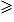 0 et g(x) − f(x)
0 et g(x) − f(x) 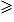 0
0Donc pour tout x de [0 ;1], h(x)
 g(x) et g(x)
g(x) et g(x)  f(x) soit h(x)
f(x) soit h(x)  g(x)
g(x)  f(x)
f(x)Et pour tout x de [1 ;
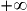 [, h(x)
[, h(x) 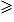 g(x) et g(x)
g(x) et g(x) 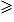 f(x) soit h(x)
f(x) soit h(x) 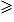 g(x)
g(x) 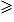 f(x)
f(x)Ainsi pour tout x de [0 ;1], x3
 x2
x2  x et pour tout x de [1 ;
x et pour tout x de [1 ; 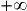 , x
, x  x2
x2  x3.
x3.6. Comment étudier le sens de variation d'une fonction résultant de l'enchaînement d'opérateurs ?
Un opérateur est une fonction qui commande une seule opération :
Par exemple :
– ajouter 2 :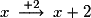 ;
;
– prendre la racine carrée :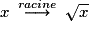 ;
;
– prendre l'opposé :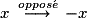 .
.
Par exemple :
– ajouter 2 :
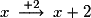 ;
;– prendre la racine carrée :
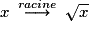 ;
;– prendre l'opposé :
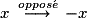 .
.Lorsque l'on connaît l'enchaînement des opérateurs, on peut facilement déterminer le sens de variation de la fonction obtenue.
Exemple
Si l'on applique successivement les opérateurs « ajouter 2 », « élever au carré », « prendre l'opposé », on obtient la fonction 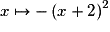 . On traduit cette décomposition par le schéma :
. On traduit cette décomposition par le schéma :
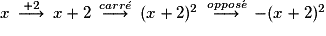 .
.
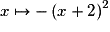 . On traduit cette décomposition par le schéma :
. On traduit cette décomposition par le schéma :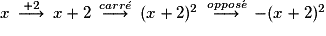 .
.Soit deux nombres a et b quelconques de l'intervalle [0 ; 5], tels que a < b, on peut écrire : 0 < a < b < 5.
On ajoute 2 à chaque membre : 2 < a + 2 < b + 2 < 7.
On élève au carré des nombres positifs, l'ordre est inchangé :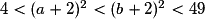 .
.
On prend les opposés, l'ordre est inversé :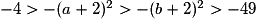 .
.
L'ordre des images de a et b par la fonction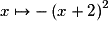 est inversé, la fonction est donc décroissante.
est inversé, la fonction est donc décroissante.
Exercice n°6
On ajoute 2 à chaque membre : 2 < a + 2 < b + 2 < 7.
On élève au carré des nombres positifs, l'ordre est inchangé :
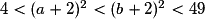 .
.On prend les opposés, l'ordre est inversé :
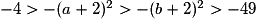 .
.L'ordre des images de a et b par la fonction
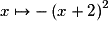 est inversé, la fonction est donc décroissante.
est inversé, la fonction est donc décroissante.Exercice n°6
À retenir
• La fonction carré, qui à tout nombre réel associe son carré, est décroissante pour les valeurs négatives de la variable et croissante pour les valeurs positives. Le passage au carré inverse l'ordre si les nombres sont négatifs et conserve l'ordre si les nombres sont positifs. La fonction carré se représente par une parabole.
• La fonction inverse, qui à tout nombre réel non nul associe son inverse, est décroissante pour les valeurs négatives et les valeurs positives de la variable. Le passage à l'inverse inverse l'ordre, que ce soit pour deux nombres positifs ou pour deux nombres négatifs (non nuls). La fonction inverse se représente par deux branches d'une hyperbole.
• En décomposant une fonction en une chaîne d'opérateurs, on peut déterminer le sens de variation d'une fonction sur un intervalle donné.
• Un nombre compris entre 0 et 1 est supérieur à son carré et inférieur à sa racine carrée. Un nombre supérieur à 1 est supérieur à sa racine carrée et inférieur à son carré.
© 2000-2025, Miscellane