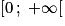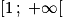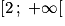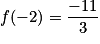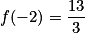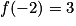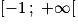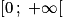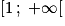Chaque fois qu'une grandeur y dépend d'une grandeur x, on dit que la première est une fonction de la seconde. Par exemple, la température est fonction de l'altitude : connaissant l'altitude, on peut calculer la température.
On va, ici, préciser cette notion de fonction, définir l'ensemble de définition d'une fonction (en effet si la variable apparaît en dénominateur ou sous un radical, certaines valeurs réelles sont alors interdites) et introduire l'étude de son sens de variation (la plupart des fonctions sont rarement monotones : leur sens de variation peut changer plusieurs fois sur leur ensemble de définition).
On va, ici, préciser cette notion de fonction, définir l'ensemble de définition d'une fonction (en effet si la variable apparaît en dénominateur ou sous un radical, certaines valeurs réelles sont alors interdites) et introduire l'étude de son sens de variation (la plupart des fonctions sont rarement monotones : leur sens de variation peut changer plusieurs fois sur leur ensemble de définition).
1. Une fonction est-elle toujours définie ?
• Une fonction numérique est une relation qui, à toute valeur d'une variable x, prise sur une partie D de l'ensemble des réels, associe une image unique y.
Si on appelle f cette fonction, on note : y = f(x).
Si on appelle f cette fonction, on note : y = f(x).
Exemple
Si une automobile consomme 10 litres aux 100 km et dispose d'un plein de 50 litres, le nombre y de litres restant dans le réservoir s'écrit en fonction du nombre x de kilomètres parcourus, selon la formule : 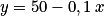 . Si on appelle f la fonction qui à x associe y, on a :
. Si on appelle f la fonction qui à x associe y, on a : 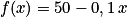 .
.
Comme l'automobiliste ne pourra pas parcourir plus de 500 kilomètres, on dira que son ensemble de définition est l'intervalle [0 ; 500] et on note![D_f = [0\,;\; 500]](https://static1.assistancescolaire.com/2/images/2_m203_m3.png) .
.
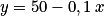 . Si on appelle f la fonction qui à x associe y, on a :
. Si on appelle f la fonction qui à x associe y, on a : 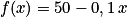 .
.Comme l'automobiliste ne pourra pas parcourir plus de 500 kilomètres, on dira que son ensemble de définition est l'intervalle [0 ; 500] et on note
![D_f = [0\,;\; 500]](https://static1.assistancescolaire.com/2/images/2_m203_m3.png) .
.• Une fonction n'est pas définie pour les valeurs qui :
– annulent son dénominateur ;
– rendent négatives une expression sous un radical.
– annulent son dénominateur ;
– rendent négatives une expression sous un radical.
Exemple
La fonction inverse (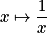 ) est définie pour tous les réels non nuls. Son ensemble de définition est donc :
) est définie pour tous les réels non nuls. Son ensemble de définition est donc : ![D = \left] { - \infty \,;\;0} \right[ \cup \left] {0\,;\; + \infty } \right[](https://static1.assistancescolaire.com/2/images/2_m203_m5.png) .
.
La fonction racine carrée (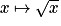 ) est définie pour tout réel positif ou nul :
) est définie pour tout réel positif ou nul : 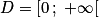 .
.
Exercice n°1
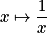 ) est définie pour tous les réels non nuls. Son ensemble de définition est donc :
) est définie pour tous les réels non nuls. Son ensemble de définition est donc : ![D = \left] { - \infty \,;\;0} \right[ \cup \left] {0\,;\; + \infty } \right[](https://static1.assistancescolaire.com/2/images/2_m203_m5.png) .
.La fonction racine carrée (
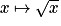 ) est définie pour tout réel positif ou nul :
) est définie pour tout réel positif ou nul : 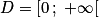 .
.Exercice n°1
2. Comment calculer une image ?
• Pour calculer l'image d'un nombre, on remplace la variable par ce nombre et on effectue les calculs en respectant les priorités opératoires.
On effectue d'abord les calculs entre parenthèses, on calcule ensuite les puissances, puis produits et quotients. On termine par les sommes algébriques.
Par exemple, pour calculer l'image de 5 par la fonction f définie sur par
par 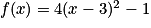 , on effectue :
, on effectue :
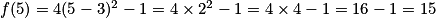 .
.
On effectue d'abord les calculs entre parenthèses, on calcule ensuite les puissances, puis produits et quotients. On termine par les sommes algébriques.
Par exemple, pour calculer l'image de 5 par la fonction f définie sur
 par
par 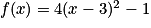 , on effectue :
, on effectue :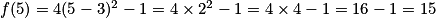 .
.• Pour compléter un tableau de valeurs, on utilise la table de la calculatrice.
Après avoir affiché la fonction, on précise les valeurs extrêmes de la variable et le pas séparant deux valeurs consécutives (sur Texas Instruments : sous la rubrique Tableset ; sur Casio : sous la rubrique Range). On peut alors faire s'afficher, sur deux colonnes, les valeurs de la variable et celles de l'image.
Par exemple, pour compléter le tableau de valeurs suivant :
Après avoir affiché la fonction, on précise les valeurs extrêmes de la variable et le pas séparant deux valeurs consécutives (sur Texas Instruments : sous la rubrique Tableset ; sur Casio : sous la rubrique Range). On peut alors faire s'afficher, sur deux colonnes, les valeurs de la variable et celles de l'image.
Par exemple, pour compléter le tableau de valeurs suivant :
3. Comment calculer un antécédent ?
• Calculer un antécédent par la fonction f d'un nombre réel a, c'est résoudre l'équation  .
.
Ainsi, chercher l'antécédent de 3 par la fonction affine f, définie sur par
par 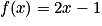 , revient à calculer la valeur de x telle que
, revient à calculer la valeur de x telle que 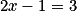 .
.
 .
.Ainsi, chercher l'antécédent de 3 par la fonction affine f, définie sur
 par
par 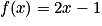 , revient à calculer la valeur de x telle que
, revient à calculer la valeur de x telle que 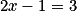 .
.• Attention, pour certaines fonctions un réel peut avoir plusieurs antécédents. Il peut aussi n'avoir aucun antécédent.
Par exemple, pour la fonction carré définie sur (
(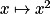 ) : 4 a pour antécédents 2 et −2 ; mais −4 n'a pas d'antécédent.
) : 4 a pour antécédents 2 et −2 ; mais −4 n'a pas d'antécédent.
Exercice n°3
Par exemple, pour la fonction carré définie sur
 (
(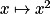 ) : 4 a pour antécédents 2 et −2 ; mais −4 n'a pas d'antécédent.
) : 4 a pour antécédents 2 et −2 ; mais −4 n'a pas d'antécédent.Exercice n°3
4. Comment détermine-t-on le sens de variation d'une fonction ?
• Soit une fonction f et I un intervalle inclus dans l'ensemble de définition de f.
• Pour qu'une fonction f soit croissante sur un intervalle I, il faut que, pour tous nombres a et b de cet intervalle tels que a < b, on ait 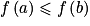 .
.
Plus directement, pour qu'une fonction soit croissante il faut et il suffit qu'elle respecte l'ordre : f(a) et f(b) doivent être rangés dans le même ordre que a et b sur l'intervalle I.
Si l'on a f(a) < f(b), c'est-à-dire une inégalité stricte, f est strictement croissante.
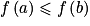 .
.Plus directement, pour qu'une fonction soit croissante il faut et il suffit qu'elle respecte l'ordre : f(a) et f(b) doivent être rangés dans le même ordre que a et b sur l'intervalle I.
Si l'on a f(a) < f(b), c'est-à-dire une inégalité stricte, f est strictement croissante.
• Pour qu'une fonction f soit décroissante sur un intervalle I, il faut que, pour tous nombres a et b de cet intervalle, tels que a < b, on ait 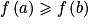 .
.
Plus directement, pour qu'une fonction soit décroissante il faut et il suffit qu'elle inverse l'ordre : f(a) et f(b) doivent être rangés dans l'ordre inverse de celui de a et b sur l'intervalle I.
Si l'on a f(a) > f(b), la fonction f est strictement décroissante.
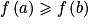 .
.Plus directement, pour qu'une fonction soit décroissante il faut et il suffit qu'elle inverse l'ordre : f(a) et f(b) doivent être rangés dans l'ordre inverse de celui de a et b sur l'intervalle I.
Si l'on a f(a) > f(b), la fonction f est strictement décroissante.
• Pour qu'une fonction f soit constante sur un intervalle I, il faut que, pour deux nombres a et b de cet intervalle tels que a < b, on ait 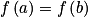 .
.
Plus directement, une fonction est constante sur un intervalle I lorsque tous les réels de cet intervalle ont la même image.
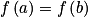 .
.Plus directement, une fonction est constante sur un intervalle I lorsque tous les réels de cet intervalle ont la même image.
Remarque
Il ne faut pas confondre le sens de variation d'une fonction et son signe. Une fonction peut être positive et décroissante, c'est le cas pour la fonction carré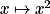 sur l'intervalle
sur l'intervalle ![]- \infty~;~0]](https://static1.assistancescolaire.com/2/images/2_m203_m18.png) . Elle peut aussi être négative et croissante, c'est le cas pour la fonction affine
. Elle peut aussi être négative et croissante, c'est le cas pour la fonction affine 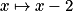 sur l'intervalle
sur l'intervalle ![]- \infty~;~2]](https://static1.assistancescolaire.com/2/images/2_m203_m20.png) .
.Exemple
Soit la fonction affine f, définie sur [-1 ; 5] par 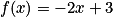 :
:
Pour tous réels a et b tels que : −1 < a < b < 5, on a :
2 > −2a > −2b > −10 ;
5 > −2a + 3 > −2b + 3 > -7 ;
soit 5 > f(b) > f(a) > −7.
Comme l'ordre est inversé, f est donc décroissante sur l'intervalle [-1 ; 5].
On peut résumer ces informations en un tableau de variation :
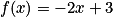 :
:Pour tous réels a et b tels que : −1 < a < b < 5, on a :
2 > −2a > −2b > −10 ;
5 > −2a + 3 > −2b + 3 > -7 ;
soit 5 > f(b) > f(a) > −7.
Comme l'ordre est inversé, f est donc décroissante sur l'intervalle [-1 ; 5].
On peut résumer ces informations en un tableau de variation :
 |
Plus directement, une fonction affine est décroissante lorsque son coefficient directeur est négatif. S'il est positif, la fonction affine est croissante.
• Un opérateur est une fonction qui commande une seule opération. Quand une fonction se décompose en une chaîne d'opérateurs, on applique successivement ces opérateurs aux nombres a et b.
Exemple
Soit la fonction f, définie sur 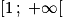 par
par 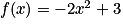 . On décompose cette fonction en opérateurs :
. On décompose cette fonction en opérateurs : 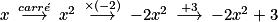 .
.
Pour 1 <a < b, on a :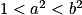 , puis
, puis 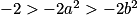 et
et 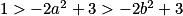 .
.
Donc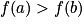 . L'ordre est inversé, on en déduit que la fonction f est décroissante sur l'intervalle
. L'ordre est inversé, on en déduit que la fonction f est décroissante sur l'intervalle 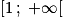 .
.
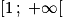 par
par 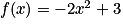 . On décompose cette fonction en opérateurs :
. On décompose cette fonction en opérateurs : 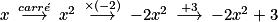 .
.Pour 1 <a < b, on a :
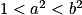 , puis
, puis 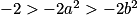 et
et 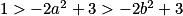 .
.Donc
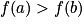 . L'ordre est inversé, on en déduit que la fonction f est décroissante sur l'intervalle
. L'ordre est inversé, on en déduit que la fonction f est décroissante sur l'intervalle 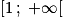 .
.5. Comment déterminer le signe d'une fonction ?
Pour savoir sur quelle partie de son ensemble de définition une fonction f est positive, on résout l'inéquation 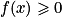 . La fonction est alors négative sur l'autre partie.
. La fonction est alors négative sur l'autre partie.
Attention : une fonction peut être positive et décroissante (comme, par exemple, la fonction :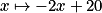 , définie sur [5 ; 10]) ou négative et croissante (comme la fonction :
, définie sur [5 ; 10]) ou négative et croissante (comme la fonction : 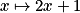 , définie sur [-10 ; -5]).
, définie sur [-10 ; -5]).
Exercice n°4
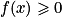 . La fonction est alors négative sur l'autre partie.
. La fonction est alors négative sur l'autre partie.Attention : une fonction peut être positive et décroissante (comme, par exemple, la fonction :
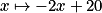 , définie sur [5 ; 10]) ou négative et croissante (comme la fonction :
, définie sur [5 ; 10]) ou négative et croissante (comme la fonction : 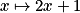 , définie sur [-10 ; -5]).
, définie sur [-10 ; -5]).Exercice n°4
Définition : Soit f une fonction numérique définie pour tout x de I (I une partie de  ).
).
On dit que f est paire si et seulement si :
I est symétrique par rapport à 0 et pour tout x de I, f(x) = f(−x).
On dit que f est impaire si et seulement si :
I est symétrique par rapport à 0 et pour tout x de I, f(−x) = −f(x).
Exemples :
La fonction carré est paire. En effet l'ensemble de définition de la fonction carré est .
.  est bien un ensemble symétrique par rapport à 0. De plus, pour tout x de
est bien un ensemble symétrique par rapport à 0. De plus, pour tout x de  :
:
(−x)2 = (−1 ×x)2 = (−1)2 ×x2 = 1 × x2 = x2
La fonction inverse est impaire. En effet l'ensemble de définition de la fonction inverse est *.
*.  * est bien un ensemble symétrique par rapport à 0. De plus, pour tout x de
* est bien un ensemble symétrique par rapport à 0. De plus, pour tout x de  * :
* :
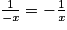
Conséquence graphique :
On munit le plan d'un repère orthogonal. Soit f une fonction numérique et Cf la courbe représentative de f dans le repère.
Si f est paire alors C f est symétrique par rapport à l'axe des ordonnées.
Si f est impaire alors C f est symétrique par rapport à l'origine du repère.
Illustration : La parabole représentant la fonction carré est bien symétrique par rapport à l'axe des ordonnées. L'hyperbole représentant la fonction inverse est bien symétrique par rapport à l'origine du repère.
Exercice n°5
 ).
).On dit que f est paire si et seulement si :
I est symétrique par rapport à 0 et pour tout x de I, f(x) = f(−x).
On dit que f est impaire si et seulement si :
I est symétrique par rapport à 0 et pour tout x de I, f(−x) = −f(x).
Exemples :
La fonction carré est paire. En effet l'ensemble de définition de la fonction carré est
 .
.  est bien un ensemble symétrique par rapport à 0. De plus, pour tout x de
est bien un ensemble symétrique par rapport à 0. De plus, pour tout x de  :
:(−x)2 = (−1 ×x)2 = (−1)2 ×x2 = 1 × x2 = x2
La fonction inverse est impaire. En effet l'ensemble de définition de la fonction inverse est
 *.
*.  * est bien un ensemble symétrique par rapport à 0. De plus, pour tout x de
* est bien un ensemble symétrique par rapport à 0. De plus, pour tout x de  * :
* :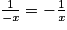
Conséquence graphique :
On munit le plan d'un repère orthogonal. Soit f une fonction numérique et Cf la courbe représentative de f dans le repère.
Si f est paire alors C f est symétrique par rapport à l'axe des ordonnées.
Si f est impaire alors C f est symétrique par rapport à l'origine du repère.
Illustration : La parabole représentant la fonction carré est bien symétrique par rapport à l'axe des ordonnées. L'hyperbole représentant la fonction inverse est bien symétrique par rapport à l'origine du repère.
Exercice n°5
À retenir
• On doit exclure de l'ensemble de définition les valeurs de la variable qui annulent les dénominateurs et le limiter à celles pour lesquelles les nombres sous les radicaux sont positifs.
• Une fonction est croissante sur un intervalle lorsque les images de tout couple de nombres a et b de cet intervalle sont dans le même ordre que ces deux nombres. Si l'ordre est inversé, la fonction est décroissante.
• On ne confondra pas le sens de variation et le signe. Une fonction peut être positive et décroissante aussi bien que négative et croissante.
Exercice n°1
L'écriture d'une fonction f est : 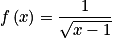 .
.
Sur lequel de ces ensembles la fonction f est-elle bien définie ?
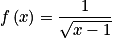 .
.Sur lequel de ces ensembles la fonction f est-elle bien définie ?
Cochez la bonne réponse.
| ||
| ||
|
Le nombre sous le radical doit être positif et le dénominateur doit être différent de 0.
On doit donc avoir la condition : x − 1 > 0, soit x > 1.
x doit être strictement plus grand que 1, donc seul l'intervalle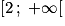 convient.
convient.
x doit être strictement plus grand que 1, donc seul l'intervalle
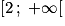 convient.
convient.Exercice n°2
Soit f une fonction définie sur 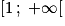 par
par 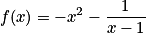 .
.
On a :
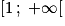 par
par 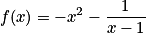 .
.On a :
Cochez la bonne réponse.
| ||
| ||
|
On remplace x par −2 dans l'écriture de f : 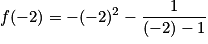 .
.
On effectue ensuite le calcul au dénominateur :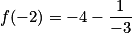 .
.
Soit :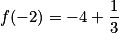 .
.
En réduisant au même dénominateur, on obtient :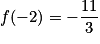 .
.
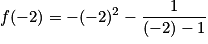 .
.On effectue ensuite le calcul au dénominateur :
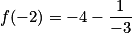 .
.Soit :
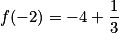 .
.En réduisant au même dénominateur, on obtient :
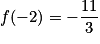 .
.Exercice n°3
La fonction f est définie sur 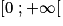 par :
par : 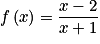 .
.
Par la fonction f :
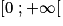 par :
par : 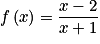 .
.Par la fonction f :
Cochez la bonne réponse.
| ||
| ||
|
Une fraction est nulle lorsque son numérateur est nul sans que son dénominateur le soit.
Le numérateur s'annule pour x = 2 et le dénominateur pour x = −1 ; donc 2 est donc le seul antécédent de 0.
Exercice n°4
La fonction f, définie sur  par
par 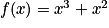 est positive sur l'intervalle :
est positive sur l'intervalle :
 par
par 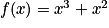 est positive sur l'intervalle :
est positive sur l'intervalle : Cochez la bonne réponse.
| ||
| ||
|
La factorisation de f s'écrit : 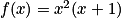 .
.
Comme un carré est toujours positif, f(x) est du signe de (x + 1).
Or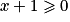 est équivalent à
est équivalent à 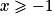 , f est donc positive sur l'intervalle
, f est donc positive sur l'intervalle 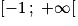 .
.
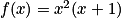 .
.Comme un carré est toujours positif, f(x) est du signe de (x + 1).
Or
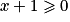 est équivalent à
est équivalent à 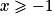 , f est donc positive sur l'intervalle
, f est donc positive sur l'intervalle 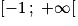 .
.Exercice n°5
Soit h la fonction définie pour tout x de R par h(x) = 1492x2 − 2019.
Cochez la bonne réponse.
| ||
| ||
|