Échantillonnage
Fiche
Pas de journal écrit ou parlé sans son sondage quotidien, avec son lot de pourcentages et de commentaires. Mais ces sondages sont-ils fiables ? Nous allons présenter ici les notions qui les sous-tendent (celles de fréquence et de simulation) et préciser les limites de leurs résultats.
1. Comment établir une distribution des fréquences d'une série statistique ?
• On part d'une série statistique représentée par un tableau du type :
| Valeur de X | 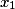 | 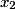 | ... | 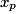 | |
| Effectif | 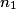 | 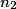 | ... | 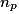 | n |
On calcule pour chaque valeur
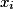 de la série la fréquence relative
de la série la fréquence relative  .
.C'est le rapport
 , soit :
, soit : 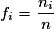 .
.• La distribution des fréquences d'une série statistique est l'ensemble des fréquences de toutes les valeurs de la série. On la donne sous forme d'un tableau :
| Valeur de X | 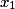 | 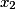 | ... | 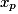 | |
| Fréquence | 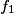 | 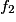 | ... | 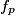 | 1 |
• Plus généralement, on appelle fréquence d'un événement la somme des fréquences des valeurs qui constituent cet événement.
Exercice n°1Exercice n°2
Exercice n°1Exercice n°2
2. Comment observer une fluctuation d'échantillonnage ?
• Quand on veut connaître la proportion p d'un caractère dans une grande population, il est long et coûteux de faire une enquête sur tous les individus. On prélève alors un échantillon.
Prélever un échantillon de taille n dans la population, c'est prendre simplement n individus (ou répéter n fois une expérience dans des conditions identiques) sur lesquels on mesure le caractère étudié.
La série statistique composée des n résultats obtenus constitue un échantillon de taille n.
Prélever un échantillon de taille n dans la population, c'est prendre simplement n individus (ou répéter n fois une expérience dans des conditions identiques) sur lesquels on mesure le caractère étudié.
La série statistique composée des n résultats obtenus constitue un échantillon de taille n.
• Cette méthode ne peut pas fournir la valeur exacte de p, car des échantillons différents peuvent donner des proportions différentes.
Si on dispose de plusieurs échantillons, on peut observer ces différences sur leurs distributions de fréquences. C'est ce qu'on appelle la fluctuation d'échantillonnage et il suffit, pour l'observer, de prélever deux échantillons.
Exercice n°3
Si on dispose de plusieurs échantillons, on peut observer ces différences sur leurs distributions de fréquences. C'est ce qu'on appelle la fluctuation d'échantillonnage et il suffit, pour l'observer, de prélever deux échantillons.
Exercice n°3
3. Comment interpréter un sondage ?
• Nous venons de dire qu'à partir d'un échantillon, on ne peut pas connaître exactement la proportion p d'un caractère sur toute la population entière.
Cependant, si on respecte certaines conditions, la fréquence observée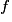 sur l'échantillon est une bonne valeur approchée de la proportion p.
sur l'échantillon est une bonne valeur approchée de la proportion p.
Ces conditions sont les suivantes :
– il faut choisir les individus au hasard ;
– il faut remettre à chaque fois l'individu choisi dans la population (ou répéter l'expérience dans des conditions identiques) ;
– il faut que la taille n de l'échantillon soit assez grande, on doit avoir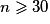 .
.
Cependant, si on respecte certaines conditions, la fréquence observée
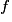 sur l'échantillon est une bonne valeur approchée de la proportion p.
sur l'échantillon est une bonne valeur approchée de la proportion p.Ces conditions sont les suivantes :
– il faut choisir les individus au hasard ;
– il faut remettre à chaque fois l'individu choisi dans la population (ou répéter l'expérience dans des conditions identiques) ;
– il faut que la taille n de l'échantillon soit assez grande, on doit avoir
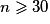 .
.• Dans ces conditions, on peut même établir que, dans au moins 95 % des cas (des échantillons observés),
4. Pourquoi et comment simuler une expérience ?
• Une expérience aléatoire est une expérience dont l'issue (le résultat) dépend du hasard.
Simuler une expérience aléatoire, c'est remplacer cette expérience par une autre expérience aléatoire qui permet de produire les résultats que l'on obtiendrait en réalisant effectivement la première expérience.
Simuler une expérience aléatoire, c'est remplacer cette expérience par une autre expérience aléatoire qui permet de produire les résultats que l'on obtiendrait en réalisant effectivement la première expérience.
• On simule une expérience quand l'expérience initiale est difficile à réaliser parce que trop coûteuse, trop longue ou difficilement observable.
En simulant une expérience plusieurs fois (c'est-à-dire en prélevant plusieurs échantillons), on espère tirer de la distribution des fréquences et de leur fluctuation quelques enseignements.
En simulant une expérience plusieurs fois (c'est-à-dire en prélevant plusieurs échantillons), on espère tirer de la distribution des fréquences et de leur fluctuation quelques enseignements.
• Pour simuler une expérience, on peut utiliser une calculatrice avec la commande RANDOM ou un tableur avec la fonction ALEA).
La fonction RANDOM d'une calculatrice nous donne au hasard un nombre entre 0 et 1 avec 10 chiffres après la virgule.
La fonction RANDOM d'une calculatrice nous donne au hasard un nombre entre 0 et 1 avec 10 chiffres après la virgule.
Exemple
Dans une urne, on a placé 35 jetons rouges et 65 jetons verts. L'expérience consiste à tirer, de cette urne, 10 jetons avec remise. N'ayant ni urne, ni jeton sous la main, comment peut-on simuler cette expérience ?On utilise la calculatrice : en appelant 10 fois de suite la fonction RANDOM, on obtient 10 nombres décimaux compris entre 0 et 1. On considère pour chaque nombre les deux premiers chiffres après la virgule. Si le nombre ainsi formé est compris entre 1 et 35, on considère qu'on a effectué un tirage d'un jeton rouge, sinon on considère que l'on a tiré un jeton vert. On peut ainsi simuler autant de fois que l'on veut notre expérience.
Exercice n°6
5. Comment simuler à l'aide de Python cent expériences de 100 lancers de dé ?
Algorithme : On va simulerer cent fois la même expérience aléatoire : « lancer cent fois un dé ». On s'intérésse à la proportion d'apparition de la face 6. On stocke les cent résultats dans une liste et on construit le nuage de points pour visualiser le résultat obtenu.
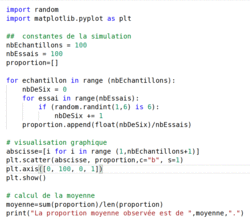 |
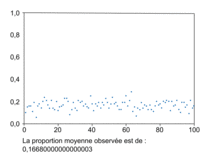 |
On obtient par exemple cet affichage :
On observe bien que la très grande majorité valeurs obtenues appartiennent à un certain intervalle, qu'on appelle intervalle de fluctuation.
À retenir
• La fréquence relative d'une valeur d'une série statistique est donnée par le rapport  .
.
 .
.• La proportion observée 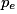 d'un caractère sur un échantillon de taille n est une valeur approchée à
d'un caractère sur un échantillon de taille n est une valeur approchée à 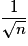 près de la proportion p du caractère sur la population entière.
près de la proportion p du caractère sur la population entière.
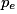 d'un caractère sur un échantillon de taille n est une valeur approchée à
d'un caractère sur un échantillon de taille n est une valeur approchée à 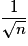 près de la proportion p du caractère sur la population entière.
près de la proportion p du caractère sur la population entière.• La touche RANDOM sur la calculatrice permet de simuler des expériences aléatoires.
© 2000-2025, Miscellane
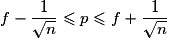 , c'est-à-dire que
, c'est-à-dire que 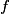 est une valeur approchée de p à
est une valeur approchée de p à 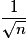 près.
près.