Probabilités
Fiche
Par une lettre du 29 juillet 1654, Pascal répond à Fermat sur le problème des « parties » (Pascal, Œuvres complètes, Gallimard, « La Pléiade », p. 77). On peut dater de ce jour la naissance des probabilités. Cette branche des mathématiques prendra son plein essor avec les Bernoulli, puis avec Poisson, jusqu'à fournir, au xxe siècle, la base théorique nécessaire à la conception des lois de toutes les sciences, de la physique à la sociologie.
1. Comment définir une probabilité ?
• On part d'une expérience aléatoire E, c'est-à-dire d'une expérience dont on peut prévoir les issues possibles, mais dont on ne connaît le résultat qu'après sa réalisation.
• Première étape : à l'aide d'un arbre, par exemple, on détermine toutes les issues possibles de l'expérience aléatoire. On définit ainsi l'univers  comme l'ensemble de toutes les issues possibles de E. On a :
comme l'ensemble de toutes les issues possibles de E. On a : 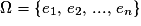
 comme l'ensemble de toutes les issues possibles de E. On a :
comme l'ensemble de toutes les issues possibles de E. On a : 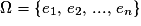
• Seconde étape : à chaque issue on attribue une probabilité, c'est-à-dire qu'à chaque 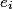 on associe un nombre
on associe un nombre 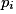 . Ces nombres doivent vérifier les conditions suivantes :
. Ces nombres doivent vérifier les conditions suivantes :
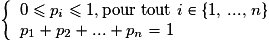 Pour déterminer les nombres
Pour déterminer les nombres 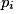 , il existe deux possibilités :
, il existe deux possibilités :
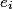 on associe un nombre
on associe un nombre 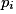 . Ces nombres doivent vérifier les conditions suivantes :
. Ces nombres doivent vérifier les conditions suivantes :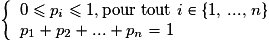 Pour déterminer les nombres
Pour déterminer les nombres 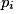 , il existe deux possibilités :
, il existe deux possibilités : - soit on associe à toutes les issues la même probabilité
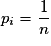 , on dit alors que la probabilité est équirépartie ou que l'on est dans une situation d' équiprobabilité ;
, on dit alors que la probabilité est équirépartie ou que l'on est dans une situation d' équiprobabilité ; - soit on répète l'expérience dans des conditions identiques, on définit alors
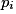 comme la fréquence de
comme la fréquence de 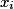 quand le nombre de répétitions tend vers
quand le nombre de répétitions tend vers 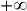 .
.
• À l'issue de ces deux étapes, on a établi la loi de probabilité que l'on présente sous forme de tableau :
| Issue | 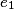 | 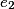 | … | 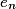 | |
| Probabilité | 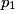 | 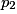 | … | 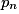 | 1 |
Remarque
La première étape est essentielle. Il s'agit d'abord de bien comprendre l'expérience, de la visualiser et de la simuler pour écrire quelques issues possibles. Il s'agit enfin de déterminer toutes les issues de l'expérience. C'est dans ce « toutes » que réside la difficulté.Exercice n°1Exercice n°2Exercice n°3
2. Comment calculer la probabilité d'un événement ?
Soit E une expérience aléatoire et 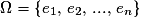 , l'univers associé à E.
, l'univers associé à E.
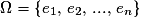 , l'univers associé à E.
, l'univers associé à E.• On appelle événement de l'expérience aléatoire E, tout sous-ensemble de  .
.
Autrement dit, un événement A est une partie de .
.
Quand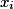 appartient à A, on dit aussi que
appartient à A, on dit aussi que 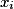 réalise A.
réalise A.
On appelle événement élémentaire, un événement constitué d'un seul élément de , c'est-à-dire constitué d'une seule issue
, c'est-à-dire constitué d'une seule issue 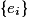 .
.
 .
.Autrement dit, un événement A est une partie de
 .
.Quand
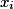 appartient à A, on dit aussi que
appartient à A, on dit aussi que 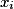 réalise A.
réalise A.On appelle événement élémentaire, un événement constitué d'un seul élément de
 , c'est-à-dire constitué d'une seule issue
, c'est-à-dire constitué d'une seule issue 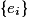 .
.• La probabilité P(A) d'un événement A est la somme des probabilités des issues qui le constituent.
Dans le cas où la probabilité est équirépartie, chaque issue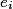 a pour probabilité
a pour probabilité 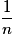 .
.
Ainsi, si A contient m éléments,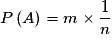 .
.
Autrement dit : P(A) est égal au rapport du nombre d'éléments de A par le nombre d'éléments de Ω.
Dans le cas où la probabilité est équirépartie, chaque issue
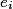 a pour probabilité
a pour probabilité 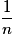 .
.Ainsi, si A contient m éléments,
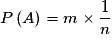 .
.Autrement dit : P(A) est égal au rapport du nombre d'éléments de A par le nombre d'éléments de Ω.
Remarques
• La probabilité d'un événement élémentaire 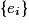 est
est 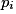 .
.
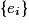 est
est 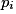 .
.•  est appelé événement certain ;
est appelé événement certain ; 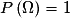 .
.
 est appelé événement certain ;
est appelé événement certain ; 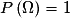 .
.• Le sous-ensemble vide, noté 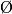 , est appelé événement impossible ;
, est appelé événement impossible ; 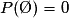 .
.
Exercice n°4Exercice n°5Exercice n°6
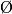 , est appelé événement impossible ;
, est appelé événement impossible ; 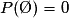 .
.Exercice n°4Exercice n°5Exercice n°6
3. Comment calculer la probabilité de l'union de deux événements ?
• Soit A et B deux événements d'une même expérience aléatoire.
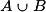 est l'événement constitué des issues qui appartiennent à A ou à B.
est l'événement constitué des issues qui appartiennent à A ou à B.
 est l'événement constitué des issues qui appartiennent à la fois à A et à B.
est l'événement constitué des issues qui appartiennent à la fois à A et à B.
Quand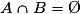 , c'est-à-dire quand aucune issue n'appartient à la fois à A et à B, on dit que A et B sont incompatibles (ou disjoints).
, c'est-à-dire quand aucune issue n'appartient à la fois à A et à B, on dit que A et B sont incompatibles (ou disjoints).
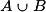 est l'événement constitué des issues qui appartiennent à A ou à B.
est l'événement constitué des issues qui appartiennent à A ou à B. est l'événement constitué des issues qui appartiennent à la fois à A et à B.
est l'événement constitué des issues qui appartiennent à la fois à A et à B.Quand
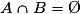 , c'est-à-dire quand aucune issue n'appartient à la fois à A et à B, on dit que A et B sont incompatibles (ou disjoints).
, c'est-à-dire quand aucune issue n'appartient à la fois à A et à B, on dit que A et B sont incompatibles (ou disjoints).• Si A et B sont quelconques : 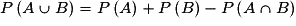 .
.
Si A et B sont incompatibles (ou disjoints) :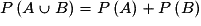 .
.
Exercice n°7Exercice n°8
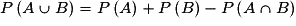 .
.Si A et B sont incompatibles (ou disjoints) :
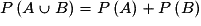 .
.Exercice n°7Exercice n°8
4. Comment calculer la probabilité d'un événement contraire ?
L'événement contraire de A, noté 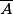 , est l'événement qui se réalise quand A n'est pas réalisé. Il est constitué des issues de
, est l'événement qui se réalise quand A n'est pas réalisé. Il est constitué des issues de  qui n'appartiennent pas à A.
qui n'appartiennent pas à A.
Cela se résume ainsi :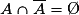 et
et 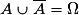 .
.
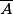 , est l'événement qui se réalise quand A n'est pas réalisé. Il est constitué des issues de
, est l'événement qui se réalise quand A n'est pas réalisé. Il est constitué des issues de  qui n'appartiennent pas à A.
qui n'appartiennent pas à A.Cela se résume ainsi :
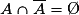 et
et 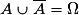 .
.• En utilisant les propriétés du paragraphe précédent, on montre que, pour tout événement A : 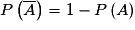 .
.
Exercice n°9Exercice n°10
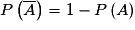 .
.Exercice n°9Exercice n°10
À retenir
• Définir une probabilité, c'est associer à chaque issue 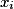 un nombre
un nombre 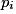 positif de telle sorte que
positif de telle sorte que 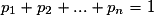 .
.
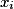 un nombre
un nombre 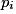 positif de telle sorte que
positif de telle sorte que 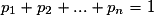 .
.• La probabilité P(A) d'un événement A est la somme des probabilités des issues qui le constituent.
• Dans le cas équiprobable : 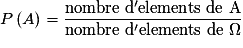 .
.
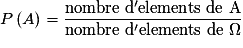 .
.• Soit A et B deux événements quelconques : 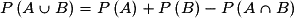 .
.
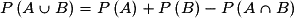 .
.• Soit A un événement quelconque : 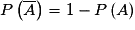 .
.
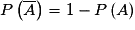 .
.© 2000-2025, Miscellane