Consulter le programme

Introduction

Intentions majeures

La classe de seconde est conçue pour permettre aux élèves de consolider leur maîtrise du socle commun de connaissances, de compétences et de culture afin de réussir la transition du collège au lycée. Elle les prépare à déterminer leur choix d'un parcours au sein du cycle terminal jusqu'au baccalauréat général ou technologique dans l'objectif d'une poursuite d'études supérieures réussie et, au-delà, de leur insertion professionnelle.
L'enseignement des mathématiques de la classe de seconde est conçu à partir des intentions suivantes :

permettre à chaque élève de consolider les acquis du collège et une culture mathématique de base, de développer son goût des mathématiques, d'en apprécier les démarches et les objets afin qu'il puisse faire l'expérience personnelle de l'efficacité des concepts mathématiques ainsi que de la simplification et de la généralisation que permet la maîtrise de l'abstraction ;
préparer au choix de l'orientation : choix de la spécialité mathématiques dans la voie générale, choix de la série dans la voie technologique ;
assurer les bases mathématiques nécessaires à toutes les poursuites d'études au lycée.

Le programme de mathématiques définit un ensemble de connaissances et de compétences qui s'appuie sur le programme de collège, en réactivant les notions déjà étudiées et en y ajoutant un nombre raisonnable de nouvelles notions, à étudier de manière suffisamment approfondie.

Compétences mathématiques

Dans le prolongement des cycles précédents, six grandes compétences sont travaillées :

chercher, expérimenter – en particulier à l'aide d'outils logiciels ;
modéliser, faire une simulation, valider ou invalider un modèle ;
représenter, choisir un cadre (numérique, algébrique, géométrique…), changer de registre ;
raisonner, démontrer, trouver des résultats partiels et les mettre en perspective ;
calculer, appliquer des techniques et mettre en œuvre des algorithmes ;
communiquer un résultat par oral ou par écrit, expliquer une démarche.

La résolution de problèmes est un cadre privilégié pour développer, mobiliser et combiner plusieurs de ces compétences. Cependant, pour prendre des initiatives, imaginer des pistes de solution et s'y engager sans s'égarer, l'élève doit disposer d'automatismes. Ceux-ci facilitent en effet le travail intellectuel en libérant l'esprit des soucis de mise en œuvre technique et élargissent le champ des démarches susceptibles d'être engagées. L'acquisition de ces réflexes est favorisée par la mise en place d'activités rituelles, notamment de calcul (mental ou réfléchi, numérique ou littéral). Elle est menée conjointement avec la résolution de problèmes motivants et substantiels, afin de stabiliser connaissances, méthodes et stratégies.

Diversité de l'activité de l'élève

La mise en œuvre du programme doit permettre aux élèves d'acquérir des connaissances, des méthodes et des démarches spécifiques.
La diversité des activités concerne aussi bien les contextes (internes aux mathématiques ou liés à des situations issues de la vie quotidienne ou d'autres disciplines) que les types de tâches proposées : « questions flash » pour favoriser l'acquisition d'automatismes, exercices d'application et d'entraînement pour stabiliser et consolider les connaissances, exercices et problèmes favorisant les prises d'initiatives, mises au point collectives d'une solution, productions d'écrits individuels ou collectifs, etc.
Il importe donc que cette diversité se retrouve dans les travaux proposés à la classe. Parmi ceux-ci, les travaux écrits faits hors du temps scolaire permettent, à travers l'autonomie laissée à chacun, le développement des qualités de prise d'initiative ou de communication ainsi que la stabilisation des connaissances et des méthodes étudiées. Ils doivent être conçus de façon à prendre en compte la diversité des élèves. Le calcul est un outil essentiel pour la résolution de problèmes. Il est important en classe de seconde de poursuivre l'acquisition d'automatismes initiée au collège. L'installation de ces automatismes est favorisée par la mise en place d'activités rituelles, notamment de calcul (mental ou réfléchi, numérique ou littéral). Elle est menée conjointement avec la résolution de problèmes motivants et substantiels, afin de stabiliser connaissances, méthodes et stratégies.

Utilisation de logiciels

L'utilisation de logiciels (calculatrice ou ordinateur), d'outils de visualisation et de représentation, de calcul (numérique ou formel), de simulation, de programmation développe la possibilité d'expérimenter, ouvre largement le dialogue entre l'observation et la démonstration et change profondément la nature de l'enseignement.
L'utilisation régulière de ces outils peut intervenir selon trois modalités :

par le professeur, en classe, avec un dispositif de visualisation collective adapté ;
par les élèves, en classe, à l'occasion de la résolution d'exercices ou de problèmes ;
dans le cadre du travail personnel des élèves hors du temps de classe (par exemple au CDI ou à un autre point d'accès au réseau local).

Évaluation des élèves

Les élèves sont évalués en fonction des capacités attendues et selon des modalités variées : devoir surveillé avec ou sans calculatrice, devoir en temps libre, rédaction de travaux de recherche, individuels ou collectifs, compte rendu de travaux pratiques pouvant s'appuyer sur des logiciels, exposé oral d'une solution. L'évaluation doit permettre de repérer les acquis des élèves en lien avec les six compétences mathématiques : chercher, modéliser, représenter, raisonner, calculer, communiquer.

Place de l'oral

Les étapes de verbalisation et de reformulation jouent un rôle majeur dans l'appropriation des notions mathématiques et la résolution des problèmes. Comme toutes les disciplines, les mathématiques contribuent au développement des compétences orales, notamment à travers la pratique de l'argumentation. Celle-ci conduit à préciser sa pensée et à expliciter son raisonnement de manière à convaincre. Elle permet à chacun de faire évoluer sa pensée, jusqu'à la remettre en cause si nécessaire, pour accéder progressivement à la vérité par la preuve. Des situations variées se prêtent à la pratique de l'oral en mathématiques : la reformulation par l'élève d'un énoncé ou d'une démarche, les échanges interactifs lors de la construction du cours, les mises en commun après un temps de recherche, les corrections d'exercices, les travaux de groupe, les exposés individuels ou à plusieurs… L'oral mathématique mobilise à la fois le langage naturel et le langage symbolique dans ses différents registres (graphiques, formules, calcul).

Trace écrite

Disposer d'une trace de cours claire, explicite et structurée est une aide essentielle à l'apprentissage des mathématiques. Faisant suite aux étapes importantes de recherche, d'appropriation individuelle ou collective, la trace écrite récapitule de façon organisée les connaissances, les méthodes et les stratégies étudiées en classe. Explicitant les liens entre les différentes notions ainsi que leurs objectifs, éventuellement enrichie par des exemples ou des schémas, elle constitue pour l'élève une véritable référence vers laquelle il peut se tourner autant que de besoin. Sa consultation régulière (notamment au moment de la recherche d'exercices et de problèmes, sous la conduite du professeur ou en autonomie) favorise à la fois la mémorisation et le développement de compétences. Le professeur doit avoir le souci de la bonne qualité (mathématique et rédactionnelle) des traces écrites figurant au tableau et dans les cahiers d'élèves. En particulier, il est essentiel de bien distinguer le statut des énoncés (conjecture, définition, propriété - admise ou démontrée -, démonstration, théorème).

Travail personnel des élèves

Si la classe est le lieu privilégié pour la mise en activité mathématique des élèves, les travaux hors du temps scolaire sont indispensables pour consolider les apprentissages. Fréquents, de longueur raisonnable et de nature variée, ces travaux sont essentiels à la
formation des élèves. Individuels ou en groupe, évalués à l'écrit ou à l'oral, ces travaux sont conçus de façon à prendre en compte la diversité des élèves et permettent le développement des qualités d'initiatives, tout en assurant la stabilisation des connaissances et des compétences.

Quelques lignes directrices pour l'enseignement

Le professeur veille à créer, dans la classe de mathématiques, une atmosphère de travail favorable aux apprentissages, combinant bienveillance et exigence. Il est important de développer chez chaque élève des attitudes positives à l'égard des mathématiques et sa capacité à résoudre des problèmes stimulants.
L'élève doit être incité à s'engager dans une recherche mathématique, individuellement ou en équipe, et à développer sa confiance en lui. Il cherche, essaie des pistes, prend le risque de se tromper. Il ne doit pas craindre l'erreur, mais en tirer profit grâce au professeur, qui l'aide à l'identifier, à l'analyser et la comprendre. Ce travail sur l'erreur participe à la construction de ses apprentissages.
Les problèmes proposés aux élèves peuvent être internes aux mathématiques, provenir de l'histoire des mathématiques, être issus des autres disciplines ou du monde réel, en prenant garde que la simple inclusion de références au monde réel ne suffit pas toujours à transformer un exercice de routine en un bon problème. Dans tous les cas, ils doivent être bien conçus et motivants, afin de développer les connaissances et compétences mathématiques du programme.
Le professeur veille à établir un équilibre entre divers temps de l'apprentissage :

les temps de recherche, d'activité, de manipulation ;
les temps de dialogue et d'échange, de verbalisation ;
les temps de cours, où le professeur expose avec précision, présente certaines démonstrations et permet aux élèves d'accéder à l'abstraction ;
les temps où sont présentés et discutés des exemples, pour vérifier la bonne compréhension de tous les élèves ;
les exercices et problèmes, allant progressivement de l'application la plus directe au thème d'étude ;
les rituels, afin de consolider les connaissances et les méthodes.

Organisation du programme

Le programme s'organise en cinq grandes parties : « Nombres et calculs », « Géométrie », « Fonctions », « Statistiques et probabilités » et « Algorithmique et programmation ». Ce découpage n'est pas un plan de cours et il est essentiel d'exploiter les possibilités d'interaction entre ces parties. Les connaissances du collège sont systématiquement réactivées à travers des problèmes.
Démontrer est une composante fondamentale de l'activité mathématique. Le programme identifie quelques démonstrations exemplaires, que les élèves découvrent selon des modalités variées : présentation par le professeur, élaboration par les élèves sous la direction du professeur, devoirs à la maison, etc.
Le programme propose un certain nombre d'approfondissements possibles, mais en aucun cas obligatoires. Ils peuvent permettre une différenciation pédagogique.
Il peut être judicieux d'éclairer le cours par des éléments de contextualisation d'ordre historique, épistémologique ou culturel. L'histoire peut aussi être envisagée comme une source féconde de problèmes clarifiant le sens de certaines notions. Les items « Histoire des mathématiques » identifient quelques possibilités en ce sens. Pour les étayer, le professeur peut s'appuyer sur l'étude de documents historiques.

Nombres et calculs

Objectifs

Cette partie prolonge le thème « Nombres et calculs » du cycle 4 avec pour objectifs de :

approfondir la connaissance des divers types et ensembles de nombres ;
développer la pratique du calcul numérique ou algébrique ;
travailler sur les inégalités ;
résoudre des problèmes modélisés par des équations ou inéquations se ramenant au premier degré.

Les élèves rencontrent les nombres réels comme abscisses des points d'une droite graduée, et plus largement comme nombres permettant de mesurer des grandeurs. Ils les comparent, ils apprennent qu'il existe des nombres irrationnels, les encadrent par des nombres décimaux ou rationnels. Ils comprennent que calculatrices et logiciels font des calculs approchés. En liaison avec un approfondissement de l'étude des multiples et diviseurs, ils consolident la pratique du calcul sur les fractions.
La mise en évidence de la puissance du calcul littéral comme outil de résolution de problème, déjà rencontrée au collège, reste un objectif important. L'élève doit être confronté à des situations, internes ou externes aux mathématiques, dans lesquelles une modélisation est nécessaire, faisant intervenir variables, expressions algébriques, équations ou inéquations. Les situations internes sont l'occasion de réactiver les connaissances du collège, notamment sur les thèmes « Espace et géométrie » et « Grandeurs et mesures » (longueurs, aires, volumes, angles, vitesses).
Il convient d'équilibrer la formation, d'une part en proposant des applications variées et significatives des notions et techniques étudiées, d'autre part, en veillant à l'acquisition des automatismes, par la pratique fréquente de calculs routiniers. 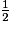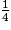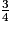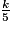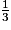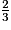On réactivera notamment les formes décimales exactes de $\frac{1}{2}$ , $\frac{1}{4}$ , $\frac{3}{4}$ et des fractions $\frac{k}{5}$ pour k dans {1,2,3,4}, et arrondies de $\frac{1}{3}$ et $\frac{2}{3}$ .

Histoire des mathématiques

La notion apparemment familière de nombre ne va pas de soi. Deux exemples : la crise provoquée par la découverte des irrationnels chez les mathématiciens grecs, la différence entre « nombres réels » et « nombres de la calculatrice ». Il s'agit également de souligner le gain en efficacité et en généralité qu'apporte le calcul littéral, en expliquant qu'une grande partie des mathématiques n'a pu se développer qu'au fur et à mesure de l'élaboration, au cours des siècles, de symbolismes efficaces. Il est possible d'étudier des textes anciens d'auteurs tels que Diophante, Euclide, Al-Khwarizmi, Fibonacci, Viète, Fermat, Descartes et mettre en évidence leurs aspects algorithmiques.

Manipuler les nombres réels

Au cycle 4, les élèves ont étudié les inégalités pour comparer des valeurs numériques. La notion d'intervalle, présentée comme ensemble de nombres vérifiant des inégalités, est nouvelle.
La notation de la valeur absolue est introduite pour exprimer la distance entre deux nombres réels et caractériser les intervalles de centre donné. Toute autre utilisation est hors programme.

Contenus

Ensemble des nombres réels, droite numérique.
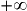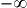Intervalles de . Notations $+\infty$ et $-\infty$ .
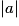Notation $\left | a \right |$ . Distance entre deux nombres réels.
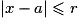Représentation de l'intervalle [a − r , a + r] puis caractérisation par la condition $\left | x-a \right | \leqslant r$ .
Ensemble 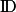des nombres décimaux. Encadrement décimal d'un nombre réel à 10 ⁻ⁿ près.
Ensemble 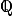des nombres rationnels. Nombres irrationnels ; exemples fournis par la géométrie, par exemple 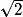$\sqrt{2}$ et π.

Capacités attendues

Associer à chaque point de la droite graduée un unique nombre réel et réciproquement.
Représenter un intervalle de la droite numérique. Déterminer si un nombre réel appartient à un intervalle donné.
Donner un encadrement, d'amplitude donnée, d'un nombre réel par des décimaux.
Dans le cadre de la résolution de problèmes, arrondir en donnant le nombre de chiffres significatifs adapté à la situation étudiée.

Démonstrations

Le nombre rationnel 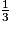$\frac{1}{3}$ n'est pas décimal.
Le nombre réel 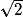$\sqrt{2}$ est irrationnel.

Exemple d'algorithme

Déterminer par balayage un encadrement de 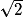$\sqrt{2}$ d'amplitude inférieure ou égale à 10 −n.

Approfondissements possibles

Développement décimal illimité d'un nombre réel.
Observation, sur des exemples, de la périodicité du développement décimal de nombres rationnels, du fait qu'un développement décimal périodique correspond à un rationnel.

Utiliser les notions de multiple, diviseur et de nombre premier

Contenus

Notations 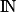et .
Définition des notions de multiple, de diviseur, de nombre pair, de nombre impair.

Capacités attendues

Modéliser et résoudre des problèmes mobilisant les notions de multiple, de diviseur, de nombre pair, de nombre impair, de nombre premier.
Présenter les résultats fractionnaires sous forme irréductible.

Démonstrations

Pour une valeur numérique de a, la somme de deux multiples de a est multiple de a.
Le carré d'un nombre impair est impair.

Exemples d'algorithme

Déterminer si un entier naturel a est multiple d'un entier naturel b.
Pour des entiers a et b donnés, déterminer le plus grand multiple de a inférieur ou égal à b.
Déterminer si un entier naturel est premier.

Utiliser le calcul littéral

Contenus

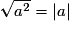Règles de calcul sur les puissances entières relatives, sur les racines carrées.Relation $\sqrt{a^{2}}=\left | a \right |$ .
Identités a² − b² = (a − b)(a + b), (a + b)² = a² + 2ab + b² et (a − b)² = a² − 2ab + b², à savoir utiliser dans les deux sens.
Exemples simples de calcul sur des expressions algébriques, en particulier sur des expressions fractionnaires.
Somme d'inégalités. Produit d'une inégalité par un réel positif, négatif, en liaison avec le sens de variation d'une fonction affine.
Ensemble des solutions d'une équation, d'une inéquation.

Capacités attendues

Effectuer des calculs numériques ou littéraux mettant en jeu des puissances, des racines carrées, des écritures fractionnaires.
Sur des cas simples de relations entre variables (par exemple U = RI, d = vt, S = πr ², V = abc, V = πr ²h), exprimer une variable en fonction des autres. Cas d'une relation du premier degré ax + by = c.
Choisir la forme la plus adaptée (factorisée, développée réduite) d'une expression en vue de la résolution d'un problème.
Comparer deux quantités en utilisant leur différence, ou leur quotient dans le cas positif.
Modéliser un problème par une inéquation.
Résoudre une inéquation du premier degré.

Démonstrations

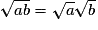Quels que soient les réels positifs a et b, on a $\sqrt{ab}=\sqrt{a}\sqrt{b}$ .
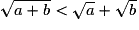
Si a et b sont des réels strictement positifs, $\sqrt{a+b}< \sqrt{a}+\sqrt{b}$
Pour a et b réels positifs, illustration géométrique de l'égalité (a + b)² = a² + 2ab + b².

Exemple d'algorithme

Déterminer la première puissance d'un nombre positif donné supérieure ou inférieure à une valeur donnée.

Approfondissements possibles

Développement de (a + b + c)².
Développement de (a + b)³.
Inégalité entre moyennes géométrique et arithmétique de deux réels strictement positifs.

Géométrie

Objectifs

Les objectifs de cette partie sont les suivants :

consolider les notions sur les configurations géométriques abordées au collège et prolonger leur étude ;
introduire les vecteurs du plan comme outil permettant d'étudier des problèmes issus des mathématiques et des autres disciplines, en particulier de la physique ;
poursuivre l'étude de la géométrie repérée, qui relie nombres, calculs algébriques, fonctions et géométrie et constitue un outil utile à d'autres disciplines. En particulier, introduire la notion d'ensemble de points du plan décrit par une équation, en explicitant le cas des équations de droites.

Les élèves découvrent les vecteurs, qui sont un outil efficace pour démontrer en géométrie et pour modéliser en physique. Ils les manipulent dans le plan muni d'un repère orthonormé. Ils approfondissent leurs connaissances sur les configurations du plan, disposent de nouveaux outils pour analyser des figures géométriques, résoudre des problèmes. Ils étudient les équations de droite, font le lien entre représentations géométrique, algébrique, et fonctionnelle.
La géométrie développe des capacités de représentation. Il importe de s'appuyer sur des figures, selon des modalités diverses (tracé à main levée, schéma, figure soignée, utilisation de logiciels). Dans le cadre de la résolution de problèmes, l'utilisation d'un logiciel de géométrie dynamique par les élèves leur donne une plus grande autonomie et encourage leur prise d'initiative.
Le programme se place dans le cadre de la géométrie plane. Cependant, le professeur peut proposer des activités mobilisant les notions de géométrie dans l'espace vues au collège (sections, aires, volumes) enrichies de celles étudiées en seconde (vecteurs).
Il convient de mettre en valeur l'intervention de la géométrie dans les autres parties du programme, notamment « Nombres et calculs » et « Fonctions ».

Histoire des mathématiques

Les progrès apportés par la « méthode des coordonnées » de Descartes, puis par la notion de vecteur, permettent de relier efficacement géométrie, physique et calcul.
On pourra évoquer les mathématiques grecques, en mettant en évidence le rôle central de la géométrie dans la naissance de l'idée de démonstration ainsi que le faible développement de l'algèbre sous l'Antiquité, en partie dû à l'appui systématique sur la géométrie.

Manipuler les vecteurs du plan

Au cycle 4, la notion de translation fait l'objet d'une première approche, fondée sur l'observation de son effet sur les configurations planes et de manipulations diverses, notamment sur un quadrillage ou à l'aide d'un logiciel de géométrie dynamique. On s'y appuie en seconde pour introduire la notion de vecteur.
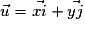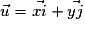Le professeur peut définir les opérations vectorielles à partir des coordonnées, ou bien commencer par leur construction géométrique. Dans tous les cas, la relation $\vec{u}=\vec{xi}+\vec{yj}$ est mise en évidence. La relation de Chasles est introduite pour illustrer l'addition des vecteurs, mais ne fait pas l'objet d'un travail spécifique.

Contenus

Vecteur 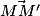$\vec{M{M}'}$ associé à la translation qui transforme M en M'. Direction, sens et norme.
Égalité de deux vecteurs. Notation 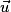$\vec{u}$ . Vecteur nul.
Somme de deux vecteurs en lien avec l'enchaînement des translations. Relation de Chasles.
Base orthonormée. Coordonnées d'un vecteur. Expression de la norme d'un vecteur.
Expression des coordonnées de 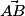$\vec{AB}$ en fonction de celles de A et de B.
Produit d'un vecteur par un nombre réel. Colinéarité de deux vecteurs.
Déterminant de deux vecteurs dans une base orthonormée, critère de colinéarité. Application à l'alignement, au parallélisme.

Capacités attendues

Représenter géométriquement des vecteurs.
Construire géométriquement la somme de deux vecteurs.
Représenter un vecteur dont on connaît les coordonnées. Lire les coordonnées d'un vecteur.
Calculer les coordonnées d'une somme de vecteurs, d'un produit d'un vecteur par un nombre réel.
Calculer la distance entre deux points. Calculer les coordonnées du milieu d'un segment.
Caractériser alignement et parallélisme par la colinéarité de vecteurs.
Résoudre des problèmes en utilisant la représentation la plus adaptée des vecteurs.

Démonstration

Deux vecteurs sont colinéaires si et seulement si leur déterminant est nul.

Approfondissement possible

Définition vectorielle des homothéties.

Résoudre des problèmes de géométrie

Contenus

Projeté orthogonal d'un point sur une droite.

Capacités attendues

Résoudre des problèmes de géométrie plane sur des figures simples ou complexes (triangles, quadrilatères, cercles).
Calculer des longueurs, des angles, des aires et des volumes.
Traiter de problèmes d'optimisation.

Démonstrations

Le projeté orthogonal du point M sur une droite Δ est le point de la droite Δ le plus proche du point M.
Relation trigonométrique 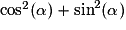$\textrm{cos}^{2}(\alpha )+\textrm{sin}^{2}(\alpha )$ dans un triangle rectangle.

Approfondissements possibles

Démontrer que les hauteurs d'un triangle sont concourantes.
Expression de l'aire d'un triangle : 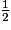$\frac{1}{2}$ ab sinC.
Formule d'Al-Kashi.
Le point de concours des médiatrices est le centre du cercle circonscrit.

Représenter et caractériser les droites du plan

Au cycle 4, les élèves ont rencontré les équations de droite pour représenter les fonctions affines. En seconde, ils étendent l'étude à la forme générale des équations de droite. Dans cette section, le plan est muni d'un repère orthonormé.

Contenus

Vecteur directeur d'une droite.
Équation de droite : équation cartésienne, équation réduite.
Pente (ou coefficient directeur) d'une droite non parallèle à l'axe des ordonnées.

Capacités attendues

Déterminer une équation de droite à partir de deux points, un point et un vecteur directeur ou un point et la pente.
Déterminer la pente ou un vecteur directeur d'une droite donnée par une équation ou une représentation graphique.
Tracer une droite connaissant son équation cartésienne ou réduite.
Établir que trois points sont alignés ou non.
Déterminer si deux droites sont parallèles ou sécantes.
Résoudre un système de deux équations linéaires à deux inconnues, déterminer le point d'intersection de deux droites sécantes.

Démonstration

En utilisant le déterminant, établir la forme générale d'une équation de droite.

Exemples d'algorithme

Étudier l'alignement de trois points dans le plan.
Déterminer une équation de droite passant par deux points donnés.

Approfondissements possibles

Ensemble des points équidistants d'un point et de l'axe des abscisses.
Représentation, sur des exemples, de parties du plan décrites par des inégalités sur les coordonnées.

Fonctions

Objectifs

Au cycle 4, les élèves ont découvert progressivement la notion de fonction, manipulé différents modes de représentation : expression algébrique, tableau de valeurs, représentation graphique, programmes de calcul. Ils connaissent le vocabulaire de base : variable, fonction, antécédent, image et la notation f(x). Selon le mode de représentation choisi, ils déterminent une image ou des antécédents d'un nombre par une fonction. Ils ont étudié les fonctions linéaires, les fonctions affines et leur représentation graphique.
En seconde, les objectifs sont les suivants :

consolider la notion de fonction, comme exprimant la dépendance d'une variable par rapport à une autre ;
exploiter divers registres, notamment le registre algébrique et le registre graphique ;
étendre la panoplie des fonctions de référence ;
étudier les notions liées aux variations et aux extremums des fonctions.

Les fonctions définies sur un intervalle de Ensemble R

permettent de modéliser des phénomènes continus. On peut confronter les élèves à des exemples de fonctions définies sur 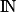Ensemble N

pour modéliser des phénomènes discrets. La notation u(n) est alors utilisée.
La modélisation d'une dépendance par une fonction apparaît dans des domaines très variés : géométrie dans le plan ou dans l'espace, biologie, économie, physique, sciences sociales. La modélisation de phénomènes dépendant du temps, la variable étant alors notée t est mise en évidence
Les outils numériques sont mis à profit :

un logiciel de géométrie dynamique, pour la représentation graphique et l'utilisation de curseurs ;
Python, le tableur ou la calculatrice, pour mettre en évidence l'aspect de programme de calcul.

Dans un premier temps, les élèves découvrent, manipulent et verbalisent certaines propriétés (parité, monotonie sur un intervalle…) sur les fonctions de référence. Ces propriétés se généralisent peu à peu aux fonctions quelconques. Leur maîtrise est un objectif de fin d'année. Leur formalisation est l'occasion d'un travail sur les quantificateurs.

Histoire des mathématiques

On peut évoquer la très lente élaboration de la notion de fonction, depuis l'Antiquité jusqu'à la codification actuelle par Dirichlet, en mettant en évidence quelques étapes importantes : Newton, Leibniz, Euler. On souligne alors l'importance de la notation algébrique.

Se constituer un répertoire de fonctions de référence

Les élèves doivent se constituer un répertoire d'images mentales des courbes représentatives des fonctions de référence, sur lesquelles s'appuyer lors de l'étude des propriétés des fonctions.

Contenus

Fonctions carré, inverse, racine carrée, cube : définitions et courbes représentatives.

Capacités attendues

Pour deux nombres a et b donnés et une fonction de référence f, comparer f(a) et f(b) numériquement ou graphiquement.
Pour les fonctions affines, carré, inverse, racine carrée et cube, résoudre graphiquement ou algébriquement une équation ou une inéquation du type f(x) = k, f(x) < k.

Démonstration

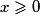Étudier la position relative des courbes d'équation y = x, y = x², y = x³, pour $x\geqslant 0$ .

Représenter algébriquement et graphiquement les fonctions

Contenus

Fonction à valeurs réelles définie sur un intervalle ou une réunion finie d'intervalles de Ensemble R

.
Courbe représentative : la courbe d'équation y = f(x) est l'ensemble des points du plan dont les coordonnées (x,y) vérifient y = f(x).
Fonction paire, impaire. Traduction géométrique.

Capacités attendues

Exploiter l'équation y = f(x) d'une courbe : appartenance, calcul de coordonnées.
Modéliser par des fonctions des situations issues des mathématiques, des autres disciplines.
Résoudre une équation ou une inéquation du type f(x) = k, f(x) < k, en choisissant une méthode adaptée : graphique, algébrique, logicielle.
Résoudre une équation, une inéquation produit ou quotient, à l'aide d'un tableau de signes.
Résoudre, graphiquement ou à l'aide d'un outil numérique, une équation ou inéquation du type f(x) = g(x), f(x) < g(x).

Approfondissement possible

Étudier la parité d'une fonction dans des cas simples.

Étudier les variations et les extremums d'une fonction

Contenus

Croissance, décroissance, monotonie d'une fonction définie sur un intervalle. Tableau de variations.
Maximum, minimum d'une fonction sur un intervalle.
Pour une fonction affine, interprétation du coefficient directeur comme taux d'accroissement, variations selon son signe.
Variations des fonctions carré, inverse, racine carrée, cube.

Capacités attendues

Relier représentation graphique et tableau de variations.
Déterminer graphiquement les extremums d'une fonction sur un intervalle.
Exploiter un logiciel de géométrie dynamique ou de calcul formel, la calculatrice ou Python pour décrire les variations d'une fonction donnée par une formule.
Relier sens de variation, signe et droite représentative d'une fonction affine.

Démonstration

Variations des fonctions carré, inverse, racine carrée.

Exemples d'algorithme

Pour une fonction dont le tableau de variations est donné, algorithmes d'approximation numérique d'un extremum (balayage, dichotomie).
Algorithme de calcul approché de longueur d'une portion de courbe représentative de fonction.

Approfondissement possible

Relier les courbes représentatives de la fonction racine carrée et de la fonction carré sur +.

Statistiques et probabilités

Objectifs

En matière d'information chiffrée, les élèves ont travaillé au cycle 4 effectifs, fréquences, proportions, pourcentages, coefficient de proportionnalité, taux d'évolution, coefficient multiplicateur. L'objectif est de consolider et de prolonger ce travail par l'étude de situations multiplicatives : proportion de proportion, évolutions successives ou réciproques. Les élèves doivent distinguer si un pourcentage exprime une proportion ou une évolution. En statistique descriptive, les élèves ont étudié moyenne, médiane et étendue. On introduit la notion de moyenne pondérée et deux indicateurs de dispersion : écart interquartile et écart type.
Au cycle 4, les élèves ont travaillé sur les notions élémentaires de probabilité : expérience aléatoire, issue, événement, probabilité. Ils ont construit leur intuition sur des situations concrètes fondées sur l'équiprobabilité, puis en simulant la répétition d'épreuves identiques et indépendantes pour observer la stabilisation des fréquences. Ils sont capables de calculer des probabilités dans des contextes faisant intervenir une ou deux épreuves.
En classe de seconde, on formalise la notion de loi (ou distribution) de probabilité dans le cas fini en s'appuyant sur le langage des ensembles et on précise les premiers éléments de calcul des probabilités. On insiste sur le fait qu'une loi de probabilité (par exemple une équiprobabilité) est une hypothèse du modèle choisi et ne se démontre pas. Le choix du modèle peut résulter d'hypothèses implicites d'équiprobabilité (par exemple, lancers de pièces ou dés équilibrés, tirage au hasard dans une population) qu'il est recommandable d'expliciter ; il peut aussi résulter d'une application d'une version vulgarisée de la loi des grands nombres, où un modèle est construit à partir de fréquences observées pour un phénomène réel (par exemple : lancer de punaise, sexe d'un enfant à la naissance). Dans tous les cas, on distingue nettement le modèle probabiliste abstrait et la situation réelle.

Histoire des mathématiques

L'histoire des probabilités fournit un cadre pour dégager les éléments de la mathématisation du hasard. Un exemple est le problème des partis, dit aussi du chevalier de Méré, l'échange de lettres entre Pascal et Fermat sur ce point puis les travaux de Pascal, Fermat et Huygens qui en découlent. Le problème du duc de Toscane ou les travaux de Leibniz sur le jeu de dés peuvent aussi être évoqués.

Utiliser l'information chiffrée et statistique descriptive

Contenus

Proportion, pourcentage d'une sous-population dans une population.
Ensembles de référence inclus les uns dans les autres : pourcentage de pourcentage.
Évolution : variation absolue, variation relative.
Évolutions successives, évolution réciproque : relation sur les coefficients multiplicateurs (produit, inverse).
Indicateurs de tendance centrale d'une série statistique : moyenne pondérée.
Linéarité de la moyenne.
Indicateurs de dispersion : écart interquartile, écart type.

Capacités attendues

Exploiter la relation entre effectifs, proportions et pourcentages.
Traiter des situations simples mettant en jeu des pourcentages de pourcentages.
Exploiter la relation entre deux valeurs successives et leur taux d'évolution.
Calculer le taux d'évolution global à partir des taux d'évolution successifs. Calculer un taux d'évolution réciproque.
Décrire verbalement les différences entre deux séries statistiques, en s'appuyant sur des indicateurs ou sur des représentations graphiques données.
Pour des données réelles ou issues d'une simulation, lire et comprendre une fonction écrite en Python renvoyant la moyenne m, l'écart type s, et la proportion d'éléments appartenant à [m − 2s,m + 2s].

Modéliser le hasard, calculer des probabilités

L'ensemble des issues est fini.

Contenus

Ensemble (univers) des issues. Événements. Réunion, intersection, complémentaire.
Loi (distribution) de probabilité. Probabilité d'un événement : somme des probabilités des issues.
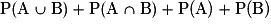Relation $\textrm{P}(\textrm{A}\cup \textrm{B})+\textrm{P}(\textrm{A}\cap \textrm{B})+\textrm{P(A)}+\textrm{P(B)}$ .
Dénombrement à l'aide de tableaux et d'arbres.

Capacités attendues

Utiliser des modèles théoriques de référence (dé, pièce équilibrée, tirage au sort avec équiprobabilité dans une population) en comprenant que les probabilités sont définies a priori.
Construire un modèle à partir de fréquences observées, en distinguant nettement modèle et réalité.
Calculer des probabilités dans des cas simples : expérience aléatoire à deux ou trois épreuves.

Échantillonnage

En liaison avec la partie « Algorithmique et programmation », on définit la notion d'échantillon. L'objectif est de faire percevoir, sous une forme expérimentale, la loi des grands nombres, la fluctuation d'échantillonnage et le principe de l'estimation d'une probabilité par une fréquence observée sur un échantillon.

Contenus

Échantillon aléatoire de taille n pour une expérience à deux issues.
Version vulgarisée de la loi des grands nombres : « Lorsque n est grand, sauf exception, la fréquence observée est proche de la probabilité. »
Principe de l'estimation d'une probabilité, ou d'une proportion dans une population, par une fréquence observée sur un échantillon.

Capacités attendues

Lire et comprendre une fonction Python renvoyant le nombre ou la fréquence de succès dans un échantillon de taille n pour une expérience aléatoire à deux issues.
Observer la loi des grands nombres à l'aide d'une simulation sur Python ou tableur.
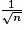Simuler N échantillons de taille n d'une expérience aléatoire à deux issues. Si p est la probabilité d'une issue et f sa fréquence observée dans un échantillon, calculer la proportion des cas où l'écart entre p et f est inférieur ou égal à . $\frac{1}{\sqrt{n}}$ .

Algorithmique et programmation

La démarche algorithmique est, depuis les origines, une composante essentielle de l'activité mathématique. Au cycle 4, en mathématiques et en technologie, les élèves ont appris à écrire, mettre au point et exécuter un programme simple. Une consolidation des acquis du cycle 4 est proposée autour de deux idées essentielles :

la notion de fonction ; la programmation comme production d'un texte dans un langage informatique.

Dans le cadre de cette activité, les élèves s'exercent à :

décrire des algorithmes en langage naturel ou dans un langage de programmation ;
en réaliser quelques-uns à l'aide d'un programme simple écrit dans un langage de programmation textuel ;
interpréter, compléter ou modifier des algorithmes plus complexes.

Un langage de programmation simple d'usage est nécessaire pour l'écriture des programmes informatiques. Le langage choisi est Python, langage interprété, concis, largement répandu et pouvant fonctionner dans une diversité d'environnements. Les élèves sont entraînés à passer du langage naturel à Python et inversement.
L'algorithmique a une place naturelle dans tous les champs des mathématiques et les problèmes ainsi traités doivent être en relation avec les autres parties du programme (fonctions, géométrie, statistiques et probabilité, logique) mais aussi avec les autres disciplines ou la vie courante.
À l'occasion de l'écriture d'algorithmes et de petits programmes, il convient de transmettre aux élèves l'exigence d'exactitude et de rigueur, et de les entraîner aux pratiques systématiques de vérification et de contrôle. En programmant, les élèves revisitent les notions de variables et de fonctions sous une forme différente.

Histoire des mathématiques

Les textes évoqués dans la thématique « Nombres et calculs » indiquent une préoccupation algorithmique tout au long de l'Histoire. Lorsqu'un texte historique a une visée algorithmique, transformer les méthodes qu'il présente en un algorithme, voire en un programme, ou inversement, est l'occasion de travailler des changements de registre qui donnent du sens au formalisme mathématique.

Utiliser les variables et les instructions élémentaires

Contenus

Variables informatiques de type entier, booléen, flottant, chaîne de caractères.
Affectation (notée ← en langage naturel).
Séquence d'instructions.
Instruction conditionnelle.
Boucle bornée (for), boucle non bornée (while).

Capacités attendues

Choisir ou déterminer le type d'une variable (entier, flottant ou chaîne de caractères).
Concevoir et écrire une instruction d'affectation, une séquence d'instructions, une instruction conditionnelle.
Écrire une formule permettant un calcul combinant des variables.
Programmer, dans des cas simples, une boucle bornée, une boucle non bornée.
Dans des cas plus complexes : lire, comprendre, modifier ou compléter un algorithme ou un programme.

Notion de fonction

Contenus

Fonctions à un ou plusieurs arguments.
Fonction renvoyant un nombre aléatoire. Série statistique obtenue par la répétition de l'appel d'une telle fonction. Capacités attendues
Écrire des fonctions simples ; lire, comprendre, modifier, compléter des fonctions plus complexes. Appeler une fonction.
Lire et comprendre une fonction renvoyant une moyenne, un écart type. Aucune connaissance sur les listes n'est exigée.
Écrire des fonctions renvoyant le résultat numérique d'une expérience aléatoire, d'une répétition d'expériences aléatoires indépendantes.

Vocabulaire ensembliste et logique

L'apprentissage des notations mathématiques et de la logique est transversal à tous les chapitres du programme. Aussi, il importe d'y travailler d'abord dans des contextes où ils se présentent naturellement, puis de prévoir des temps où les concepts et types de raisonnement sont étudiés, après avoir été rencontrés plusieurs fois en situation.
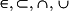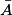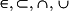Les élèves doivent connaître les notions d'élément d'un ensemble, de sous-ensemble, d'appartenance et d'inclusion, de réunion, d'intersection et de complémentaire, et savoir utiliser les symboles de base correspondant : $\in ,\subset ,\cap, \cup$ , ainsi que la notation des ensembles de nombres et des intervalles. Ils rencontrent également la notion de couple. 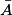Pour le complémentaire d'un sous-ensemble A de E, on utilise la notation des probabilités $\bar{A}$ , ou la notation E \ A.
Les élèves apprennent en situation à :

reconnaître ce qu'est une proposition mathématique, à utiliser des variables pour écrire des propositions mathématiques ;
lire et écrire des propositions contenant les connecteurs « et », « ou » ;
formuler la négation de propositions simples (sans implication ni quantificateurs) ;
mobiliser un contre-exemple pour montrer qu'une proposition est fausse ;
formuler une implication, une équivalence logique, et à les mobiliser dans un raisonnement simple ;
formuler la réciproque d'une implication ;
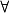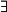lire et écrire des propositions contenant une quantification universelle ou existentielle (les symboles $\forall$ et $\exists$ sont hors programme).

Par ailleurs, les élèves produisent des raisonnements par disjonction des cas et par l'absurde.