Énoncé
Étude d'un véhicule électrique (10 points)
Les voitures électriques deviennent de nouveaux acteurs du transport, en représentant une alternative à l'utilisation des énergies fossiles. Elles présentent l'avantage de ne pas émettre de dioxyde de carbone lors de leur utilisation. L'achat de ces véhicules ne cesse d'augmenter ces dernières années.
L'objectif de cet exercice est d'étudier la charge de la batterie d'un véhicule électrique à partir d'une borne de recharge, et sa décharge lors de la circulation du véhicule sur une autoroute.
L'objectif de cet exercice est d'étudier la charge de la batterie d'un véhicule électrique à partir d'une borne de recharge, et sa décharge lors de la circulation du véhicule sur une autoroute.
1. Étude de la charge d'un véhicule électrique avec une borne de recharge
Le propriétaire d'une voiture électrique veut charger la batterie de son véhicule alors que la jauge d'autonomie de la batterie indique 20 %. Pour cela, il utilise une borne de recharge qui fournit une puissance constante de 7,40 kW en délivrant un courant électrique d'intensité constante de 32,0 A.
Les batteries lithium-ion
Les batteries utilisées couramment dans les véhicules électriques, mais également dans d'autres applications comme les téléphones portables, sont de type lithium-ion. Elles présentent l'avantage d'avoir une très grande énergie massique, comprise entre 90 et 180 Wh·kg−1. De plus, ces batteries, même partiellement déchargées, délivrent toujours la même puissance, ce qui permet une utilisation dans les mêmes conditions, quel que soit le niveau de charge.
Quelques caractéristiques du véhicule électrique étudié
Source : d'après brochure du site https://www.renault.fr/vehicules/vehicules-electriques/zoe.html
État de charge de la batterie d'un véhicule électrique
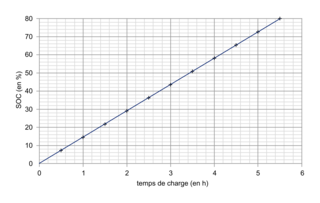
Le SOC (State Of Charge) représente l'état de charge d'une batterie et varie de 0 % (batterie "vide") à 100 % (batterie entièrement chargée). Le SOC est directement lié à l'énergie emmagasinée par la batterie. L'énergie maximale qui peut être emmagasinée représente son énergie utilisable.
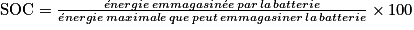 .
.
Évolution du SOC (entre 0 et 80 %) en fonction du temps de charge pour la borne de recharge utilisée
Les batteries lithium-ion
Les batteries utilisées couramment dans les véhicules électriques, mais également dans d'autres applications comme les téléphones portables, sont de type lithium-ion. Elles présentent l'avantage d'avoir une très grande énergie massique, comprise entre 90 et 180 Wh·kg−1. De plus, ces batteries, même partiellement déchargées, délivrent toujours la même puissance, ce qui permet une utilisation dans les mêmes conditions, quel que soit le niveau de charge.
Quelques caractéristiques du véhicule électrique étudié
| BATTERIE | |
| Énergie utilisable (kWh) | 41 |
| Technologie | lithium-ion |
| Tension totale (en V) | 400 |
| Nombre de cellules | 192 |
| Masse de la batterie (en kg) | 305 |
| MASSE DU VÉHICULE À VIDE (en kg) | 1480 |
Source : d'après brochure du site https://www.renault.fr/vehicules/vehicules-electriques/zoe.html
État de charge de la batterie d'un véhicule électrique
Le SOC (State Of Charge) représente l'état de charge d'une batterie et varie de 0 % (batterie "vide") à 100 % (batterie entièrement chargée). Le SOC est directement lié à l'énergie emmagasinée par la batterie. L'énergie maximale qui peut être emmagasinée représente son énergie utilisable.
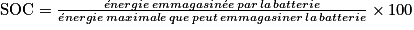 .
.Évolution du SOC (entre 0 et 80 %) en fonction du temps de charge pour la borne de recharge utilisée
 |
Donnée :
1,0 Wh = 3,6 × 103 J.
1,0 Wh = 3,6 × 103 J.
1.1. Calculer l'énergie massique maximale de la batterie de la voiture à partir des caractéristiques du véhicule électrique. Commenter.
L'énergie massique est l'énergie par unité de masse de batterie.
1.2. Montrer que l'énergie emmagasinée par la batterie lors de sa charge pour passer d'un SOC de 20 % à 80 % vaut environ 25 kWh.
Il faut isoler l'énergie emmagasinée dans la relation donnant le calcul du SOC. Le SOC passe ici de 20 % à 80 %.
1.3. Définir le rendement de la charge, puis le calculer. Commenter cette valeur.
Le rendement correspond au rapport entre l'énergie utilisable et l'énergie qui a été fournie. L'énergie qui a été fournie est à calculer avec les données de l'énoncé.
On peut schématiser la conversion d'énergie du circuit de charge de la batterie lorsque le véhicule passe d'un SOC de 20 % à un SOC de 80 % de la manière suivante :
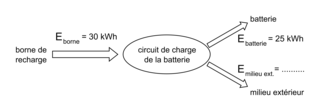 |
1.4.1. Donner la valeur manquante du schéma ci-dessus (sans le recopier sur la copie) en expliquant votre démarche.
L'énergie donnée par la borne sert à charger la batterie, mais il y a également des pertes qui vont vers le milieu extérieur.
L'énergie libérée vers le milieu extérieur est due à la présence d'une résistance Rcharge dans le circuit de charge.
1.4.2. En déduire la valeur de la résistance Rcharge. Commenter.
L'énergie libérée vers le milieu extérieur est une énergie dissipée par effet Joule, à cause de la présence de la résistance.
2. Décharge de la batterie du véhicule électrique lors de son utilisation
Le propriétaire du véhicule électrique, dont la batterie est suffisamment chargée, emprunte une autoroute horizontale et roule à la vitesse constante de 100 km·h−1 pendant une durée de 5,0 min.
On suppose que les accessoires de la voiture (climatisation, autoradio, électronique, navigateur, etc.) consomment une puissance constante de 400 W.
Existence de frottements lorsque le véhicule roule
Lorsqu'une voiture roule à une vitesse donnée, il existe deux causes principales de dissipation de l'énergie mécanique fournie par le moteur : les frottements mécaniques en lien avec les différents mouvements associés au roulement de la voiture (parties mobiles liées à la transmission, roues, pneus, etc.) et les frottements fluides (ou aérodynamiques) liés au déplacement de l'air autour de la voiture. Les frottements fluides dépendent de l'aérodynamisme de la voiture, et leur action sur le véhicule peut être modélisée par une force de frottement fluide de sens opposé à celui du vecteur vitesse de la voiture.
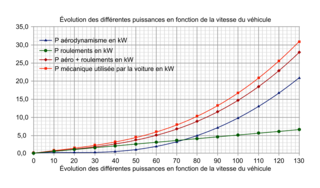
Évolution des différentes puissances en fonction de la vitesse du véhicule
On suppose que les accessoires de la voiture (climatisation, autoradio, électronique, navigateur, etc.) consomment une puissance constante de 400 W.
Existence de frottements lorsque le véhicule roule
Lorsqu'une voiture roule à une vitesse donnée, il existe deux causes principales de dissipation de l'énergie mécanique fournie par le moteur : les frottements mécaniques en lien avec les différents mouvements associés au roulement de la voiture (parties mobiles liées à la transmission, roues, pneus, etc.) et les frottements fluides (ou aérodynamiques) liés au déplacement de l'air autour de la voiture. Les frottements fluides dépendent de l'aérodynamisme de la voiture, et leur action sur le véhicule peut être modélisée par une force de frottement fluide de sens opposé à celui du vecteur vitesse de la voiture.
Évolution des différentes puissances en fonction de la vitesse du véhicule
 |
2.1. Étude d'un programme de calculateur
Les voitures électriques sont généralement équipées d'un calculateur. Un exemple possible de codage d'un calculateur, lorsque la batterie possède un état de charge de 100 %, est proposé ci-dessous :
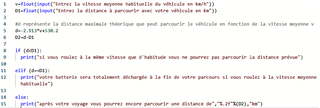 |
2.1.1. Expliquer brièvement ce que calcule ce programme.
Le script donné teste plusieurs conditions en fonction de la distance maximale théorique.
2.1.2. Modifier le programme afin de tenir compte de l'état de charge de la batterie.
Il faut prévoir une ligne de code pour entrer la valeur du SOC en pourcentage, et une modification de la distance maximale théorique en fonction de cette valeur.
2.2. Étude mécanique du déplacement de la voiture
On s'intéresse au système {voiture} en mouvement dans le référentiel terrestre.
2.2.1. Comparer, à la vitesse de 100 km·h−1 les différentes puissances intervenant dans le bilan énergétique du fonctionnement de la voiture.
Utiliser le graphique et les données de l'énoncé pour comparer les différentes puissances.
2.2.2. Calculer la distance parcourue par la voiture pendant la durée du trajet étudié.
Les données se trouvent dans l'énoncé. Attention aux unités.
2.2.3. Calculer l'énergie dissipée par les frottements fluides (ou aérodynamiques) pendant la durée du trajet étudié. En utilisant la notion de travail, déduire, à cette vitesse, la valeur de l'intensité de la force modélisant les frottements fluides. Commenter.
L'énergie est calculée à partir de la puissance dissipée par les frottements fluides. Le théorème de conservation de l'énergie (la variation de l'énergie mécanique d'un système, en mouvement entre deux points A et B, est égale à la somme des travaux des forces non conservatives) permettra de calculer la force modélisant les frottements fluides qui est une force non conservative.
Corrigé
1.1. D'après la caractéristique du véhicule électrique étudié, l'énergie utilisable de la batterie est E = 41 kWh et la masse de la batterie est m = 305 kg.
Donc, l'énergie massique maximale de la batterie est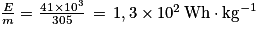 . Le résultat trouvé est en concordance avec l'énoncé qui précise que les batteries lithium-ion ont une énergie massique comprise entre 90 et 180 Wh·kg−1.
. Le résultat trouvé est en concordance avec l'énoncé qui précise que les batteries lithium-ion ont une énergie massique comprise entre 90 et 180 Wh·kg−1.
Donc, l'énergie massique maximale de la batterie est
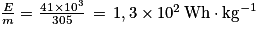 . Le résultat trouvé est en concordance avec l'énoncé qui précise que les batteries lithium-ion ont une énergie massique comprise entre 90 et 180 Wh·kg−1.
. Le résultat trouvé est en concordance avec l'énoncé qui précise que les batteries lithium-ion ont une énergie massique comprise entre 90 et 180 Wh·kg−1.1.2. La relation est 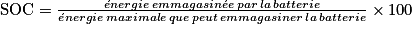 . Soit :
. Soit :
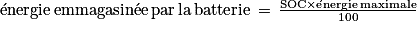 .
.
Le SOC évolue de 20 à 80 % : la batterie se charge de 60 % et l'énergie maximale correspond à l'énergie utilisable de la batterie.
Numériquement,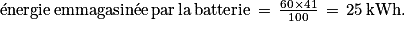
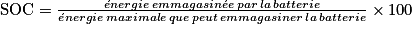 . Soit :
. Soit :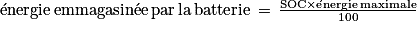 .
.Le SOC évolue de 20 à 80 % : la batterie se charge de 60 % et l'énergie maximale correspond à l'énergie utilisable de la batterie.
Numériquement,
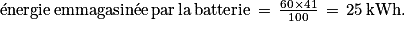
1.3. Le rendement sera 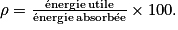
L'énergie utile est l'énergie emmagasinée par la batterie lors de la charge, soit 25 kWh.
L'énergie absorbée Eabs est à calculer avec les données de l'énoncé. Le propriétaire utilise une borne de puissance constante de 7,40 kW. De plus, pour passer d'un SOC de 20 % à 80 %, il faudra un temps de charge de t = 4 h (déterminé sur le graphique). On a donc Eabs = P × t = 7,40 × 4,0 = 30 kWh.
D'où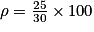 = 84 %. On peut noter qu'il y a des pertes lors de la charge de la batterie, puisque le rendement n'est pas de 100 %.
= 84 %. On peut noter qu'il y a des pertes lors de la charge de la batterie, puisque le rendement n'est pas de 100 %.
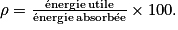
L'énergie utile est l'énergie emmagasinée par la batterie lors de la charge, soit 25 kWh.
L'énergie absorbée Eabs est à calculer avec les données de l'énoncé. Le propriétaire utilise une borne de puissance constante de 7,40 kW. De plus, pour passer d'un SOC de 20 % à 80 %, il faudra un temps de charge de t = 4 h (déterminé sur le graphique). On a donc Eabs = P × t = 7,40 × 4,0 = 30 kWh.
D'où
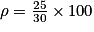 = 84 %. On peut noter qu'il y a des pertes lors de la charge de la batterie, puisque le rendement n'est pas de 100 %.
= 84 %. On peut noter qu'il y a des pertes lors de la charge de la batterie, puisque le rendement n'est pas de 100 %.1.4.1. Une partie de l'énergie absorbée par la batterie (qui est donnée par la borne) est réellement utile, et une autre partie constitue les pertes : Eabs = Eutile + Eperte.
D'où Eperte = Eabs − Eutile = 30 − 25 = 5 kWh.
D'où Eperte = Eabs − Eutile = 30 − 25 = 5 kWh.
1.4.2. L'énergie dissipée par effet Joule s'écrit EJ = Rcharge × I2 × t. D'où 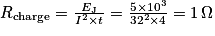 .
.
On peut noter que la valeur de la résistance est très faible, ce qui limite les pertes.
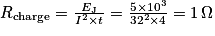 .
.On peut noter que la valeur de la résistance est très faible, ce qui limite les pertes.
2.1.1. Le script du programme donné calcule, en fonction de la vitesse moyenne entrée par l'utilisateur à la ligne 1, la distance maximale théorique. Il indiquera si la distance à parcourir est possible ou non, avec la vitesse moyenne entrée.
2.1.2. La ligne à ajouter pour demander la valeur du SOC à l'utilisateur est la suivante :
soc = float(input("Entrez la valeur de charge de la batterie en %"))
Il faut modifier la valeur de la ligne 5 (calcul de la distance maximale théorique)
d = (−2.913*v+530.2)*soc/100
soc = float(input("Entrez la valeur de charge de la batterie en %"))
Il faut modifier la valeur de la ligne 5 (calcul de la distance maximale théorique)
d = (−2.913*v+530.2)*soc/100
2.2.1. Les différentes puissances intervenant dans le bilan énergétique du fonctionnement de la voiture sont :
- la puissance mécanique utilisée par la voiture, qui est de 16,5 kW ;
- la puissance perdue par aérodynamique (10 kW) et par les roulements (5 kW), qui est de 15 kW ;
- la puissance consommée par les accessoires de la voiture, qui est de 400 W .
2.2.2. La distance parcourue pour un véhicule allant à 100 km·h−1 pendant 5 min est :
d = v × t =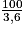 × 5 × 60 = 8333,33 m = 8,33 km.
× 5 × 60 = 8333,33 m = 8,33 km.
d = v × t =
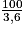 × 5 × 60 = 8333,33 m = 8,33 km.
× 5 × 60 = 8333,33 m = 8,33 km.2.2.3. L'énergie dissipée par les frottements fluides pendant ces 5 min est :
ΔE = P × Δt = 10 × 103 × 5 × 60 = 3,0 × 106 J
Or la variation d'énergie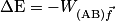 où AB est le déplacement, soit
où AB est le déplacement, soit 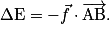
D'où Δ\mathrm{E} = f × AB, la force modélisant les frottements fluides étant opposée au déplacement.
Donc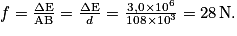
La valeur de la force de frottement équivaudrait à la force qu'exerce une masse d'environ 2,8 kg sur le sol. Elle est donc relativement faible.
ΔE = P × Δt = 10 × 103 × 5 × 60 = 3,0 × 106 J
Or la variation d'énergie
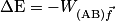 où AB est le déplacement, soit
où AB est le déplacement, soit 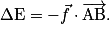
D'où Δ\mathrm{E} = f × AB, la force modélisant les frottements fluides étant opposée au déplacement.
Donc
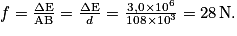
La valeur de la force de frottement équivaudrait à la force qu'exerce une masse d'environ 2,8 kg sur le sol. Elle est donc relativement faible.

