Modèles ondulatoire et particulaire de la lumière

Fiche

La lumière peut être considérée comme une onde électromagnétique. C'est grâce aux ondes électromagnétiques que l'on peut communiquer : la radio, la télévision, le wifi et le réseau 4G ou 5G utilisent les ondes électromagnétiques. Mais pour expliquer d'autres types de phénomènes physiques comme les spectres de raies d'émission des atomes, il faut considérer la lumière comme un assemblage de petit grain appelé photons.

I. Les ondes électromagnétiques

Grandeurs caractéristiques

• Une onde électromagnétique est caractérisée par plusieurs grandeurs physiques.

La longueur d'onde (λ) : elle correspond à la période spatiale de l'onde. Elle est caractéristique de chaque onde. L'unité est le mètre (m).
La période (T) : elle représente le temps nécessaire pour que l'onde effectue un cycle. L'unité est la seconde.
La fréquence (ν) : c'est l'inverse de la période (f= 1/T), elle traduit le nombre de cycles par unité de temps. Elle s'exprime en Hertz (Hz), un hertz équivalant à une oscillation par seconde.

• Ces trois grandeurs sont reliées par la relation suivante :
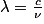
$\lambda = \frac{c}{\nu }$
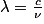
où :

λ est la longueur d'onde de l'onde électromagnétique en mètre ;
c est la célérité appelée aussi vitesse de la lumière (3.10⁸ m.s⁻¹) ;
ν (lettre grecque « nu ») est la fréquence de l'onde en Hertz.

• Par conséquent, plus la longueur d'onde est petite, plus la fréquence est élevée, et inversement.

• L'onde lumineuse résulte de la propagation d'une onde électromagnétique dans les milieux transparents. Les ondes lumineuses périodiques sont appelées des radiations.

• La propagation des ondes lumineuses ne nécessite pas de support matériel. La lumière peut se propager dans le vide contrairement aux ondes mécaniques.
Exercice n°1

Spectre des ondes électromagnétiques

• Le spectre électromagnétique représente la répartition des ondes électromagnétiques en fonction de leur longueur d'onde, de leur fréquence ou bien de leur énergie.

Les différents domaines de radiations

• Les rayons gamma (γ) : ils possèdent des longueurs d'onde inférieures à 5 nanomètres et sont invisibles. Ils sont émis par des atomes radioactifs. Très énergétiques, ils traversent facilement la matière et sont très dangereux. Ils peuvent causer de graves dégâts aux êtres vivants : mutations génétiques, brûlures des tissus. Rien ne les arrête sauf une forte épaisseur de plomb.

• Les rayons X : ils ont des longueurs d'onde comprises entre 0,001 nanomètre et 10 nanomètres. Leur rayonnement est très énergétique et il traverse plus ou moins facilement les corps matériels. Ils sont un peu moins nocifs que les rayons gamma. Ils sont utilisés en médecine pour les radiographies et dans l'industrie notamment lors du contrôle des bagages dans le transport aérien.

• Les ultraviolets : ils ont des longueurs d'onde comprises entre 100 nanomètres et 400 nanomètres ; ils sont invisibles. Leur rayonnement reste assez énergétique et ils peuvent être nocifs pour la peau. Une grande part des ultraviolets est stoppée par la couche d'ozone atmosphérique qui sert de bouclier protecteur.

• On distingue :

les UVA (400 nm-315 nm) : les UVA, dont la longueur d'onde est relativement longue, représentent près de 95 % du rayonnement UV qui atteint la surface de la Terre. Ils parviennent à traverser une vitre et pénétrer la peau jusqu'au derme. Ils sont responsables de l'effet de bronzage immédiat. En outre, ils favorisent également le vieillissement de la peau et l'apparition de rides ;
les UVB (315-280 nm) : les UVB, de longueur d'onde moyenne, ont une activité biologique importante, mais ne pénètrent pas au-delà des couches superficielles de la peau. Une partie des UVB solaires est filtrée par l'atmosphère. Ils sont responsables du bronzage et des brûlures à retardement. Outre ces effets à court terme, ils favorisent le vieillissement de la peau et l'apparition de cancers cutanés. En revanche, ils peuvent être bénéfiques pour certains types de pathologies de la peau telles que le psoriasis ou la synthèse de vitamine D ;
les UVC (280-100 nm) : les UVC, de courte longueur d'onde, sont les UV les plus nocifs, mais ils sont complètement filtrés par la couche d'ozone de l'atmosphère et n'atteignent donc théoriquement pas la surface de la Terre. Toutefois, des lampes UVC sont utilisées en laboratoire de biologie pour les effets germicides, afin de stériliser des pièces ou des appareils.

• Le domaine visible : il correspond à la partie très étroite du spectre électromagnétique perceptible par notre œil. C'est dans cette portion du spectre que l'on peut distinguer l'ensemble des couleurs de l'arc-en-ciel, du bleu au rouge.

• Il s'étend de 400 nanomètres (lumière bleue) à 800 nanomètres (lumière rouge).

• L'infrarouge (IR) : le domaine de l'infrarouge est étendu puisqu'il couvre les longueurs d'onde de 800 nanomètres à 1 millimètre. On distingue 4 types d'infrarouges : infrarouge proche, infrarouge moyen, infrarouge thermique et infrarouge lointain. De nombreuses utilisations des ondes infrarouges sont faites : vision nocturne, chauffage, détecteur d'intrusion, télécommandes, spectroscopie chimique, détecteur de faux de billets de banque.

• Les micro-ondes : les longueurs de ces ondes s'étendent d'environ 1 millimètre à plusieurs centimètres, et leurs fréquences s'étendent de 300 gigahertz à 300 mégahertz environ. Les micro-ondes sont utilisées dans de nombreux domaines : les radars, la télévision par câble, le wifi, le Bluetooth, les fours à micro-ondes… Les technologies employant des micro-ondes peuvent s'avérer dangereuses lorsqu'elles dépassent une certaine puissance. C'est pour cela qu'un four à micro-ondes ne doit pas laisser sortir les ondes.

• Les ondes radio : ce domaine de longueurs d'onde est le plus vaste du spectre électromagnétique et concerne les ondes qui ont les plus basses fréquences (inférieur à 300 gigahertz). Il s'étend des longueurs d'onde de plusieurs dizaines de centimètres à plusieurs kilomètres. Relativement faciles à émettre et à recevoir, les ondes radio sont utilisées pour la transmission de l'information, comme dans les technologies wifi ou Bluetooth, et celle utilisée pour le téléphone portable. La bande FM des postes de radio correspond à des longueurs d'onde de l'ordre du mètre.
Exercice n°2 Exercice n°3

II. Variation d'énergie dans un atome

Le photon

• Dès 1900, Max Planck postule que l'énergie ne peut s'échanger que par « paquets », ou quanta. À une onde électromagnétique monochromatique de fréquence ν, il associe un quantum d'énergie de valeur :
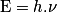
$\mathrm{E} = h . \nu$
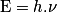
où h = 6,63.10⁻³⁴ J.s est la constante de Planck et c, la célérité de la lumière.

• En 1905, Albert Einstein postule que ces quanta d'énergie sont portés par des particules de masse nulle qu'il appelle photons. Chaque photon possède donc une énergie.
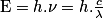
$\mathrm{E} = h . \nu = h.\frac{c}{\mathit{\lambda} }$
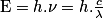
où ν est la fréquence de l'onde monochromatique associée (en hertz) et λ sa longueur d'onde (en mètre).
Exercice n°4

Postulats de Bohr

• En 1913, Niels Bohr postule que :

les variations d'énergie de l'atome sont quantifiées ;
l'atome ne peut exister que dans certains états d'énergie bien identifiés, caractérisés par des niveaux d'énergie ;
un photon de fréquence ν_n,q est émis lorsque l'atome effectue une transition entre deux niveaux d'énergie de E_n à E_q.

• L'énergie du photon est :
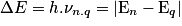
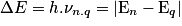
$\Delta E = h.\nu _{n.q}=\left | \mathrm{E}_{n}-\mathrm{E}_{q} \right |$

• L'atome change de niveau d'énergie par à-coups.

• Si l'atome reçoit un photon d'énergie inférieure à (E_n − E_q), la transition n'a pas lieu.

Conséquences de la quantification des niveaux d'énergie d'un atome : les spectres d'émission

• On appelle spectre d'une lumière, l'ensemble des radiations dont elle est constituée, radiations caractérisées par leurs longueurs d'onde dans le vide. Le spectre est le résultat de la décomposition de la lumière par un système dispersif (prisme ou réseau).

• Lorsqu'un atome passe d'un niveau d'énergie élevée Eⁿ à un niveau d'énergie plus faible E^q, l'atome perd de l'énergie qu'il peut émettre sous forme de rayonnement. La fréquence ν d'un rayonnement émis est donnée par la relation :
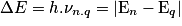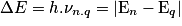$\Delta E = h.\nu _{n.q}=\left | \mathrm{E}_{n}-\mathrm{E}_{q} \right |$ .

• Toutes les transitions entre les niveaux d'énergie de l'atome sont envisageables.

• Les fréquences émises sont déterminées par les niveaux d'énergie. Ainsi, sur un spectre d'émission atomique, chaque raie monochromatique correspond à une transition entre deux niveaux d'énergie.

• Les niveaux d'énergie de l'atome ne dépendent que de sa nature : celui-ci émet des radiations qui lui sont propres et qu'il est par ailleurs capable d'absorber. Le spectre d'émission, comme le diagramme de niveaux d'énergie, est caractéristique de l'atome.

Conséquences de la quantification des niveaux d'énergie d'un atome : les spectres d'absorption

• Lorsqu'un atome passe d'un niveau de faible énergie E^q à un niveau d'énergie Eⁿsupérieure à E^q, l'atome absorbe l'énergie du rayonnement si la fréquence ν de celui-ci est proportionnelle à la différence d'énergie E_n − E_q (h étant la constante de proportionnalité).

• Si hν est inférieure à toutes les différences d'énergie envisageables, le rayonnement traverse la matière sans perturbation. Si elle est supérieure à l'une des différences d'énergies, l'excédent d'énergie est conféré à l'électron sous forme d'énergie cinétique.

• De la même manière que pour le spectre d'émission, la fréquence ν d'un rayonnement reçu est donnée par la relation :
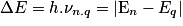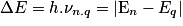$\Delta E = h.\nu _{n.q}=\left | \mathrm{E}_{n}-E_{q} \right |$ .

• Si on analyse la lumière en sortie du dispositif, on obtient le spectre d'absorption de la matière étudiée.

• Remarque : le spectre d'absorption est complémentaire du spectre d'émission : l'atome absorbe les rayonnements de longueurs d'onde identiques à celles des rayonnements qu'il est capable d'émettre par désexcitation.

Cas de l'atome d'hydrogène

• L'atome d'hydrogène est le plus simple de tous (un seul électron). Il est formé d'un proton autour duquel tourne un électron.

• Il possède une énergie potentielle E_p, qui est choisie conventionnellement nulle lorsque l'électron est à une distance infinie du noyau. Il possède une énergie cinétique E_c, car l'électron est en mouvement. Son énergie totale est E = (E_p + E_c) < 0.

• Les énergies des niveaux d'énergie de l'atome d'hydrogène sont données par la formule générale :
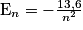$\mathrm{E}_{n} = -\frac{13,6}{n^{2}}$ ,
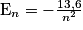avec E_n en eV (1 eV = 1,6.10⁻¹⁹ J) et n le nombre quantique principal, indiquant aussi le numéro de la couche électronique sur laquelle se situe l'électron.

• Toutes les raies du spectre d'émission d'un atome peuvent être classées en séries. Une série est constituée des raies aboutissant à un même niveau d'énergie (série de Lyman…). Pour l'atome d'hydrogène, les quatre raies les plus intenses sont dans le visible. On peut visualiser la transition correspondante sur le diagramme de niveaux d'énergie ; elles ont pour longueur d'onde : 656 nm (rouge), 486 nm (bleu), 434 nm (indigo) et 410 nm (violet).

À savoir et savoir réaliser :

Connaître les domaines des ondes électromagnétiques.
Connaître la relation entre longueur d'onde, célérité de la lumière et fréquence.
Savoir utiliser une échelle de fréquences ou de longueurs d'onde pour identifier un domaine spectral.
Citer l'ordre de grandeur des fréquences ou des longueurs d'onde des ondes électromagnétiques utilisées dans divers domaines d'application (imagerie médicale, optique visible, signaux wifi, micro-ondes, etc.).
Savoir ce que sont un photon et l'énergie d'un photon.
Connaître la description qualitative de l'interaction lumière-matière : absorption et émission.
Connaître la quantification des niveaux d'énergie des atomes.
Savoir utiliser l'expression donnant l'énergie d'un photon.
Exploiter un diagramme de niveaux d'énergie en utilisant les relations λ = c /ν et ΔE = hν.