Les fluides représentent les liquides ou les gaz. En fait, on appelle fluide tout ce qui n'est pas solide. Mais le sable s'écoule comme un liquide et pourtant il est constitué de solides. De même, les glaciers apparaissent solides à notre échelle, mais sur une échelle de temps de l'ordre du siècle, ils s'écoulent. Ce sont tous des fluides selon l'échelle de temps considéré.
I. Les propriétés des fluides
Définition
• Un fluide (liquide ou gaz) est un ensemble de particules microscopiques occupant un volume dont la géométrie s'adapte au récipient qui le contient.
• Ainsi un liquide occupe un volume limité par une surface libre tandis qu'un gaz diffuse dans tout l'espace qui lui est offert.
Séparation des échelles
• Les fluides sont constitués d'entités élémentaires, atomes ou molécules. Compte tenu du nombre de ces entités, il est difficile de prendre en compte les mouvements individuels de chaque atome ou de chaque molécule constituant le fluide. À l'échelle humaine, nous ne voyons pas individuellement les molécules, mais on peut appréhender leur mouvement d'ensemble à notre échelle, qui est appelée « échelle macroscopique ».
• On peut ainsi considérer que les molécules suffisamment voisines ont le même mouvement d'ensemble, et ne diffèrent que par des mouvements d'agitation thermique aléatoires. Dans ce cas, il est possible de trouver un petit volume spatial contenant suffisamment de molécules pour effectuer une moyenne de grandeurs microscopiques (échelle des molécules ou des atomes) sur ce volume. Ce dernier doit rester suffisamment petit pour permettre d'étudier les variations macroscopiques.
• Ainsi, on parle d'échelle mésoscopique, ou méso-échelle, qui permet de rendre compte du comportement moyen d'un grand nombre d'entités chimiques. Ce volume contenant un grand nombre d'entités chimiques s'appelle une « particule de fluide ».
• Par conséquent, à l'échelle mésoscopique, on définit encore les grandeurs macroscopiques, comme la pression, la température. et on considère la matière comme homogène. Ainsi, à cette échelle, le fluide qui est constitué d'unités microscopiques est un milieu continu et on pourra considérer que les grandeurs massiques, les grandeurs molaires ou les grandeurs volumiques varient continûment.
La masse volumique
• À l'échelle macroscopique, on définit la masse volumique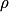 
comme étant la masse de fluide par unité de volume :
,
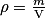où m est la masse en kilogramme du volume considéré,
V est le volume de fluide en m3,
et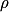
est en 
.
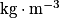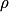comme étant la masse de fluide par unité de volume :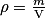,où m est la masse en kilogramme du volume considéré,
V est le volume de fluide en m3,
et
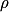est en 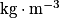.La pression
• Les particules de fluide sont en mouvement désordonné. À chaque instant, certaines molécules du fluide vont taper et rebondir sur les parois du récipient contenant le fluide. La force moyenne qu'exerce le fluide sur la paroi, exercée perpendiculairement à celle-ci et rentrant dans le système subissant la force de la part du fluide, est appelée « force de pression ».
• La force de pression est proportionnelle à la surface considérée. Il est donc commode de définir une force par unité de surface, appelée « pression ». Elle est exprimée en pascal (Pa)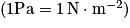 
. Comme l'orientation de cette force est parfaitement définie, un scalaire suffit pour la définir.
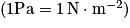. Comme l'orientation de cette force est parfaitement définie, un scalaire suffit pour la définir.• La pression atmosphérique est égale à patm = 101 325 Pa.
La température
• La température représente l'énergie d'agitation des entités chimiques du milieu considéré. Dans la pratique, la température d'un milieu est repérée par un thermomètre, dont les versions les plus traditionnelles utilisent la dilatation d'un liquide.
• Elle se mesure en Kelvin (K). Elle est reliée à la valeur en degré Celsius par :T(K) = T(°C) + 273,15.
• Le zéro absolu, exprimé en kelvin, correspond à la plus petite valeur que peut prendre la température soit 0 K = −273,15 °C.
II. La loi de Boyle-Mariotte
Qu'est-ce qu'un gaz parfait ?
• Un gaz parfait est constitué de molécules ponctuelles n'exerçant aucune interaction à distance.
La loi de Boyle-Mariotte
• Si sa température ne varie pas et que sa quantité de matière reste constante, alors le produit de la pression d'un gaz parfait par son volume reste constant. On a :
.
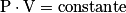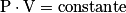.Conséquences de la loi de Boyle-Mariotte
• Cette relation indique que si l'une des grandeurs augmente alors l'autre diminue :
- si la pression diminue, alors le volume augmente et inversement si la pression augmente le volume diminue ;
- si le volume diminue (lorsque l'on compresse), alors la pression augmente, et inversement si le volume augmente alors la pression diminue.
• Si l'une des grandeurs est divisée par un nombre, l'autre sera multipliée par le même nombre :
- si la pression est multipliée par deux, alors le volume est divisé par deux, et inversement si le volume est multiplié par deux alors la pression est divisée par deux ;
- si la pression est multipliée par trois, alors le volume est divisé par trois, et inversement si le volume est multiplié par trois alors la pression est divisée par trois ;
- etc.
• Si un volume V1 de gaz à la pression P1 est amené à un état tel qu'il occupera un volume V2 et aura une pression P2, alors la loi de Boyle-Mariotte s'écrit :
.
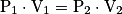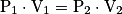.• Cette relation est valable si les pressions et les volumes ont même unité.
Exercice n°1
Exercice n°1
III. La force pressante
Définition et caractéristiques
• C'est une force de poussée exercée par un fluide sur un autre corps.
• Elle est représentée par un vecteur dont les caractéristiques sont les suivantes :
- point d'application : la force est répartie en surface. Sa résultante s'applique au centre de la surface de contact ;
- direction : suivant une direction perpendiculaire à la surface de contact ;
- sens : du fluide vers l'autre corps : elle pousse ;
- valeur : elle dépend de la pression et de la surface de contact.
• Pour une surface S en contact avec un fluide à la pression P, en tout point de cette surface, la force pressante F exercée par le fluide sur cette surface est donnée par la relation :
F = P × S,
où F est la force pressante en Newton (N),
S est la surface en mètre carré (m2),
P est la pression en pascal (Pa).
F = P × S,
où F est la force pressante en Newton (N),
S est la surface en mètre carré (m2),
P est la pression en pascal (Pa).
• La relation n'est applicable que si la pression est identique en tout point d'une surface, elle ne pourra pas être appliquée à la paroi latérale d'un récipient.
Exercice n°2
Exercice n°2
La poussée d'Archimède
On considère un corps plongé dans un fluide. La pression au sein du fluide n'est pas uniforme, car elle dépend de la profondeur. On appelle « poussée d'Archimède », la résultante des forces pressantes exercées par un fluide en équilibre dans le champ de pesanteur sur un corps entièrement immergé dans ce fluide.L'énoncé du principe d'Archimède qui décrit cette poussée est le suivant : « Tout corps immergé subit une force de poussée verticale orientée vers le haut dont la valeur correspond au poids du volume d'eau déplacé. »
Dans le cas, le plus courant, où la masse volumique du fluide ? peut être considérée constante, on obtient :
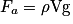,où Fa est la poussée d'Archimède en Newton (N),
ρ est la masse volumique du fluide en kilogramme par mètre cube
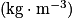,V est le volume du fluide déplacé, c'est-à-dire le volume du corps en mètre cube (m3),
g est la valeur du champ de pesanteur.
Exercice n°3
IV. Loi fondamentale de la statique des fluides
Pression absolue et pression relative
• La pression absolue est la pression mesurée par rapport au vide (c'est-à-dire l'absence totale de matière). Elle est toujours positive.
• La pression relative se définit par rapport à la pression atmosphérique existant au moment de la mesure : la valeur de la pression peut donc être positive si la pression est supérieure à la pression atmosphérique ou négative si la pression est inférieure à la pression atmosphérique. Ainsi on a la relation suivante :
Pabsolue = Prelative + Patm.
Pabsolue = Prelative + Patm.
• La mesure de la pression se fait avec un manomètre qui mesure la pression relative.
La loi fondamentale de la statique des fluides
• On considère un liquide immobile incompressible à l'intérieur d'un récipient ; la pression en tout point du liquide situé sur un même plan horizontal est identique.
 |
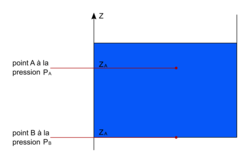Pression sur un liquide
• La loi fondamentale de la statique des fluides s'écrit, pour deux points A et B aux pressions respectives PA et PB et aux altitudes respectives zA et zA :
PB − PA = pg (zA − zB)
où PA et PB sont en pascal (Pa),
ρ est la masse volumique du liquide en kg
m-3,
g est le champ de pesanteur,
zA et zB sont en mètre (m).
PB − PA = pg (zA − zB)
où PA et PB sont en pascal (Pa),
ρ est la masse volumique du liquide en kg
m-3,g est le champ de pesanteur,
zA et zB sont en mètre (m).
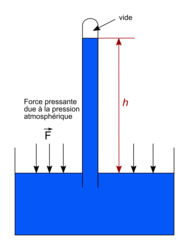
Le baromètre à mercure
• Un baromètre à mercure est constitué d'un long tube rempli de mercure plongé dans un récipient contenant également du mercure. La pression en haut de la colonne vaut zéro. Avec la relation de la loi fondamentale de la statique des fluides, on obtient :
Patm = pgh.
Patm = pgh.
• Connaissant la hauteur du mercure dans la colonne, on en déduit la pression atmosphérique.
 |
À savoir et savoir réaliser
- Connaître les échelles de description.
- Expliquer qualitativement le lien entre les grandeurs macroscopiques de description d'un fluide et le comportement microscopique des entités qui le constituent.
- Connaître les grandeurs macroscopiques de description d'un fluide au repos : masse volumique, pression et température.
- Connaître et savoir utiliser la loi de Mariotte.
- Connaître et exploiter la relation F = P.S pour déterminer la force pressante exercée par un fluide sur une surface plane S soumise à la pression P.
- Dans le cas d'un fluide incompressible au repos, utiliser la relation fournie exprimant la loi fondamentale de la statique des fluides : P2 − P1 = ρg(z1− z2).
Une image à connaître
 |
Archimède aurait fait la fameuse découverte dans son bain.
Un livre à consulter
Œuvres de Mr. Mariotte, de l'Académie Royale des Sciences, 1717
Le livre original dans lequel ont été définies les premières lois de la mécanique des fluides. À lire gratuitement sur Gallica |
Exercice n°1
Un volume de 1,00 L de gaz est libéré au niveau du plancher océanique où règne une pression P1 = 50,0 bar.
Quel est le volume de ce gaz lorsqu'il atteint la surface de l'océan ?
Données : Patm = 1,01325 × 105 Pa et 1 bar = 100 000 Pa.
Quel est le volume de ce gaz lorsqu'il atteint la surface de l'océan ?
Données : Patm = 1,01325 × 105 Pa et 1 bar = 100 000 Pa.
Cochez la bonne réponse.
| ||
| ||
| ||
|
On suppose que la température du gaz libéré ne varie pas, alors la loi de Boyle-Mariotte devient :
P1 = 50,0 bar = 50,0 × 105 Pa.
V1 = 1,00 L.
P2 = Patm = 1,01325 × 105Pa.
Or,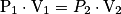
d'où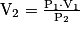 
,
soit numériquement :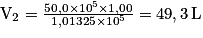
avec 3 chiffres significatifs.
P1 = 50,0 bar = 50,0 × 105 Pa.
V1 = 1,00 L.
P2 = Patm = 1,01325 × 105Pa.
Or,
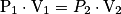d'où 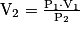,soit numériquement :
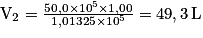avec 3 chiffres significatifs.Exercice n°2
Une personne exerce une force d'intensité 40 N avec un marteau sur la tête d'un clou. La tête du clou à une surface de 60 mm2 et la pointe du clou de 1,5 mm2.
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
| ||
|
105 Pa.
103 Pa.
105 Pa.
105 Pa.
105 Pa.
107 Pa.La force pressante a pour expression : F = P × S donc la pression est donnée par :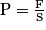 
.
Sur la tête du clou de surface S = 60 mm2 = 60 × 10-6m2,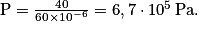
Sur la pointe du clou de surface S = 1,5 mm2 = 1,5 × 10-6m2, P =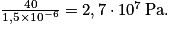
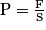.Sur la tête du clou de surface S = 60 mm2 = 60 × 10-6m2,
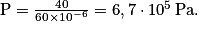
Sur la pointe du clou de surface S = 1,5 mm2 = 1,5 × 10-6m2, P =
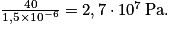
Exercice n°3
Quelle est la valeur de la poussée d'Archimède qui s'exerce sur une sphère de rayon R = 15 cm, de masse volumique 7 800 kg.m−3, d'épaisseur e = 8 mm.
Données : la masse volumique de l'eau est ρeau = 1 000 kg/m3 ; le volume d'une sphère est :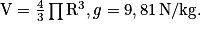
Données : la masse volumique de l'eau est ρeau = 1 000 kg/m3 ; le volume d'une sphère est :
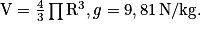
Cochez la bonne réponse.
| ||
| ||
| ||
|
La poussée d'Archimède est égale au poids du volume de fluide déplacé. La sphère a un volume
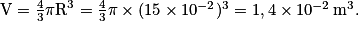
La poussée d'Archimède est donc donnée par la relation :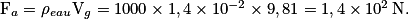
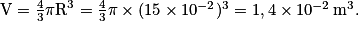
La poussée d'Archimède est donc donnée par la relation :
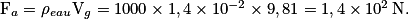
Exercice n°4
Une cuve ayant la forme d'un cylindre de rayon R = 2,00 m et de hauteur h = 3,00 m est remplie d'eau. Quelle est la valeur de la force pressante exercée sur le fond de la cuve par l'eau ?
Données : ρeau = 1,01325 × 105 Pa, ρeau = 1 000 kg/m3, g = 9,81 N/kg.
Données : ρeau = 1,01325 × 105 Pa, ρeau = 1 000 kg/m3, g = 9,81 N/kg.
Cochez la bonne réponse.
| ||
| ||
| ||
|
La force pressante a pour expression : P × S où P est la pression de l'eau en bas de la cube et S la surface du fond de la cuve.
La surface est donc S = π.R2S = π.2,002 = 12,6 m2.
La pression peut être calculée avec la loi fondamentale de la statique des fluides : PB + ρg(zA − zB).
Soit PB = ρgh + Patm, car en prenant ZA = 0 m, alors zB = −h.
Numériquement : PB = 1 000 × 9,81 × 3,00 + 1,01325 × 105 = 1,31 × 105 Pa,
et enfin F = 1,31 ×105 12,6 = 1,64.106N.
La surface est donc S = π.R2S = π.2,002 = 12,6 m2.
La pression peut être calculée avec la loi fondamentale de la statique des fluides : PB + ρg(zA − zB).
Soit PB = ρgh + Patm, car en prenant ZA = 0 m, alors zB = −h.
Numériquement : PB = 1 000 × 9,81 × 3,00 + 1,01325 × 105 = 1,31 × 105 Pa,
et enfin F = 1,31 ×105 12,6 = 1,64.106N.
Exercice n°5
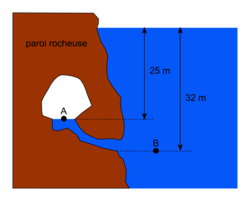
Le schéma ci-dessous représente une cavité dans un lac. Un plongeur atteint le point A dans la cavité, tandis qu'un autre plongeur l'attend au point B. Quelle est la pression en A et quelle est la pression en B ?
Données : Patm = 1,01325 × 105 Pa, ρeau = 1 000 kg/m3, g = 9,81 N/kg.
Données : Patm = 1,01325 × 105 Pa, ρeau = 1 000 kg/m3, g = 9,81 N/kg.
 |
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
La pression peut être calculée avec la loi fondamentale de la statique des fluides : P2 − P1 = pg(z1 − z2),
soit PA + Patm, car en prenant Z1 = 0 alors Z2 = −hA.
Numériquement : PA = 1 000 × 9,81 × 25 + 1,01325 × 105 = 3,47 × 105 Pa.
De même, on calcule : PB = ρghB + Patm, car en prenant Z1 = 0 alors Z2 = −hB.
Numériquement : PA = 1 000 × 9,81 × 32 + 1,01325 × 105 = 4,15 × 105 Pa.
soit PA + Patm, car en prenant Z1 = 0 alors Z2 = −hA.
Numériquement : PA = 1 000 × 9,81 × 25 + 1,01325 × 105 = 3,47 × 105 Pa.
De même, on calcule : PB = ρghB + Patm, car en prenant Z1 = 0 alors Z2 = −hB.
Numériquement : PA = 1 000 × 9,81 × 32 + 1,01325 × 105 = 4,15 × 105 Pa.
