Interactions fondamentales et champs
Fiche
La cohésion de la matière (noyaux, atomes et molécules, phases condensées ou gazeuses, organismes vivants, systèmes astronomiques) est assurée par trois interactions fondamentales : l'interaction forte, de courte portée, qui contrebalance la répulsion entre protons et assure ainsi la cohésion des noyaux ; l'interaction électromagnétique qui, par son aspect électrique, est responsable de la cohésion des atomes, des molécules et des phases condensées ; l'interaction gravitationnelle qui, bien que d'intensité beaucoup plus faible que les autres, gouverne la structure de la matière à grande échelle.
I. Les particules élémentaires
Les constituants de la matière : les protons, les neutrons et les électrons
La matière est constituée de trois particules : les protons, les neutrons et les électrons.Charge élémentaire
• Une charge électrique est une grandeur algébrique (avec un signe) qui se mesure en Coulomb (symbole C). L'électron porte une charge électrique e = − 1,6.10−19 C.
• La charge, la plus petite connue, est appelée charge élémentaire et notée e.
• Toute charge électrique q est un multiple de la charge élémentaire : q = n.e (où n est un entier).
• Les particules élémentaires s'associent pour former des atomes. Un atome est constitué d'un noyau de nucléons et d'un nuage d'électrons. Le noyau est donc chargé positivement et le nuage électronique chargé négativement. L'atome est électriquement neutre (ou de charge nulle), car il possède autant de protons que d'électrons.
II. Interactions fondamentales
La cohésion de la matière est assurée par trois interactions fondamentales :
L'interaction forte à l'échelle du noyau
• Dans un noyau atomique, les protons exercent les uns sur les autres des forces de répulsions électrostatiques qui devraient faire éclater le noyau. Il existe donc une force qui n'est ni électrostatique ni gravitationnelle et qui assure la cohésion du noyau d'un atome : l'interaction forte.
• L'interaction forte, bien que 100 à 1 000 fois plus forte que l'interaction électromagnétique, n'est pas familière, car son action ne dépasse pas les dimensions du noyau.
L'interaction électromagnétique à l'échelle de la matière jusqu'à notre échelle
• Loi de Coulomb : Deux charges ponctuelles qA et qB, placées dans le vide ou dans l'air, séparées d'une distance d, exercent l'une sur l'autre des forces 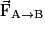 et
et 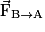 , de même direction, de sens opposés et de même valeur :
, de même direction, de sens opposés et de même valeur :
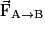 et
et 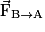 , de même direction, de sens opposés et de même valeur :
, de même direction, de sens opposés et de même valeur :•  où k = 9.109 USI.
où k = 9.109 USI.
 où k = 9.109 USI.
où k = 9.109 USI.• Ces forces sont attractives si les charges sont de signes contraires et répulsives si les charges sont de même signe.
• L'électrisation consiste à faire apparaître sur un corps :
- un excès d'électrons, alors le corps se charge négativement ;
- un défaut d'électrons, alors le corps se charge positivement.
• On peut électriser deux corps par frottement.
Exemple : Le polychlorure de vinyle ou PVC arrache des électrons de la laine. Le PVC se charge négativement et la laine se charge positivement. Le frottement fait passer des électrons d'un corps à l'autre.
• On peut électriser un corps par contact.
Exemple : Le PVC électrisé précédemment touche une boule d'aluminium. Lors du contact des électrons passent sur la boule.
• On peut électriser un corps par déplacement interne de charges.
Exemple : Le PVC électrisé précédemment s'approche, sans la toucher, d'une boule d'aluminium. La boule est attirée. La distribution des charges dans le métal est localement distordue.
• Dans un conducteur, des porteurs de charge(s) (des électrons dans les métaux, des ions dans les solutions) peuvent se déplacer dans tout l'échantillon alors que dans un isolant les électrons ne sont pas libres de se déplacer.
L'interaction gravitationnelle à l'échelle astronomique
Loi de Newton
• Deux corps ponctuels, de masse mA et mB, séparés d'une distance d (en mètre), exercent l'un sur l'autre des forces attractives 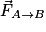 et
et 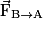 , de même direction, de sens opposés et de même valeur :
, de même direction, de sens opposés et de même valeur :
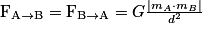 où G = 6,67.10−11
où G = 6,67.10−11 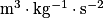 .
.
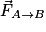 et
et 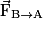 , de même direction, de sens opposés et de même valeur :
, de même direction, de sens opposés et de même valeur :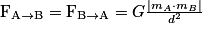 où G = 6,67.10−11
où G = 6,67.10−11 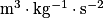 .
.• L'interaction gravitationnelle, bien que d'intensité beaucoup plus faible que les autres, gouverne la structure de la matière à grande échelle, car elle est de longue portée et toujours attractive (donc cumulative). La prédominance habituelle de l'interaction gravitationnelle sur Terre est expliquée par la quasi-neutralité électrique des objets macroscopiques et la grande masse de la Terre. On remarque de plus que l'interaction gravitationnelle est négligeable entre deux objets de taille ordinaire.
Comparaison de la loi de gravitation de Newton et de la loi de Coulomb.
• Analogie des deux lois : elles sont toutes les deux en 1/r2.
• Différence : la force de gravitation est toujours attractive, la force électrique est soit attractive, soit répulsive. Elles n'ont pas le même ordre de grandeur.
• Dans les problèmes d'attraction ou de répulsion électrostatique, on pourra négliger la force de gravitation.
III. Champ
Champ scalaire
• Un champ est une grandeur physique associée à chaque point de l'espace considéré. Une grandeur scalaire, comme la température, est définie par un nombre et une unité. L'ensemble des valeurs d'une grandeur scalaire en chaque point de l'espace définit le champ scalaire de cette grandeur.
• Si, pour un espace donné, un champ a même valeur en tout point, alors ce champ est dit uniforme.
Champ vectoriel
• Pour connaître le vent, il faut connaître la valeur de sa vitesse, mais aussi sa direction et son sens. L'ensemble de ces trois informations correspond à une grandeur vectorielle.
• L'ensemble des vecteurs d'une grandeur vectorielle en chaque point de l'espace définit le champ vectoriel de cette grandeur.
Comment caractériser un champ ?
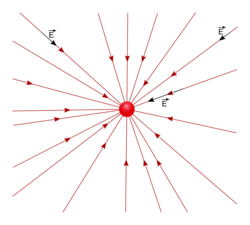
• Les lignes de champ d'un champ vectoriel sont les courbes tangentes au vecteur champ en chacun de leurs points. Elles sont orientées dans le sens du vecteur champ. Elles sont orientées par une flèche dans le même sens que celui du champ.
• Les lignes de champ électrostatique partent de la source si la charge est positive et inversement, elles entrent dans la source si la charge est négative. Les lignes de champ de gravitation sont toujours orientées du point considéré vers la masse.
 |
 |
• Un champ vectoriel uniforme est tel que le vecteur champ est le même en tout point, c'est-à-dire qu'il a la même direction, et même sens et la même norme. Les lignes de champ d'un champ uniforme sont des droites parallèles.
Le champ électrostatique
• Une charge q subit, de la part d'autres charges, une force électrostatique 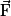 . Il existe donc un champ électrostatique noté
. Il existe donc un champ électrostatique noté 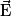 . On peut écrire :
. On peut écrire :
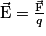
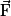 . Il existe donc un champ électrostatique noté
. Il existe donc un champ électrostatique noté 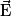 . On peut écrire :
. On peut écrire :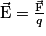
• Les caractéristiques du vecteur champ électrostatique en un point sont donc les suivantes :
- Direction : celle de la force subie par la charge q ;
- Sens : celui de sa force subie par la charge si celle-ci est positive et inversement ;
- Norme : en N.C−1 ou V.m−1.
• En utilisant un condensateur plan constitué de deux plans parallèles, l'un chargé positivement et l'autre négativement, appelés les armatures. Le champ électrostatique créé est uniforme entre les armatures. Si U est la tension entre les deux armatures et d la distance les séparant :
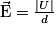 .
.
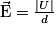 .
.Le champ de gravitation et champ de pesanteur
• Lorsqu'un objet A de masse mA est placé à proximité d'un objet B de masse mB, l'objet A subit une force gravitationnelle exercée par l'objet B.
• On peut alors définir au point où elle se trouve, un champ vectoriel appelé champ de gravitation :
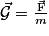 ,
,
soit numériquement :
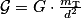 .
.
où d est la distance au centre de la planète considérée, ici la Terre (en mètre), G la constante universelle de gravitation : G = 6,67.10−11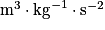 et mT la masse de la planète, ici la Terre.
et mT la masse de la planète, ici la Terre.
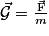 ,
,soit numériquement :
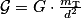 .
.où d est la distance au centre de la planète considérée, ici la Terre (en mètre), G la constante universelle de gravitation : G = 6,67.10−11
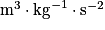 et mT la masse de la planète, ici la Terre.
et mT la masse de la planète, ici la Terre.• Tout objet placé à proximité de la Terre subit une force appelée poids de l'objet et notée 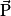 . À proximité de la Terre, tout objet ponctuel permet de détecter, à l'endroit où il est placé et grâce au poids qu'il subit, un champ vectoriel appelé champ de pesanteur que l'on note
. À proximité de la Terre, tout objet ponctuel permet de détecter, à l'endroit où il est placé et grâce au poids qu'il subit, un champ vectoriel appelé champ de pesanteur que l'on note 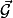 . En chaque point à proximité de la Terre, on peut écrire :
. En chaque point à proximité de la Terre, on peut écrire :

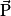 . À proximité de la Terre, tout objet ponctuel permet de détecter, à l'endroit où il est placé et grâce au poids qu'il subit, un champ vectoriel appelé champ de pesanteur que l'on note
. À proximité de la Terre, tout objet ponctuel permet de détecter, à l'endroit où il est placé et grâce au poids qu'il subit, un champ vectoriel appelé champ de pesanteur que l'on note 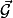 . En chaque point à proximité de la Terre, on peut écrire :
. En chaque point à proximité de la Terre, on peut écrire :
• On en déduit les caractéristiques du champ de pesanteur :
- direction : verticale ;
- sens : vers le bas ;
- norme : elle s'exprime en N.kg−1 ou m.s−2.
• La valeur de la norme du champ 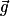 à la surface de la Terre est appelée intensité de la pesanteur et notée g. La valeur est g = 9,81 N.kg−1 environ.
à la surface de la Terre est appelée intensité de la pesanteur et notée g. La valeur est g = 9,81 N.kg−1 environ.
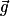 à la surface de la Terre est appelée intensité de la pesanteur et notée g. La valeur est g = 9,81 N.kg−1 environ.
à la surface de la Terre est appelée intensité de la pesanteur et notée g. La valeur est g = 9,81 N.kg−1 environ.• En négligeant la rotation de la Terre sur elle-même et l'attraction gravitationnelle exercée par la Lune et le Soleil, on peut considérer que le champ de pesanteur terrestre 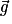 est identique au champ de gravitation créé par la Terre
est identique au champ de gravitation créé par la Terre 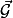 , soit
, soit 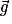 =
=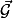 .
.
Exercice n°1Exercice n°2Exercice n°3Exercice n°4
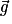 est identique au champ de gravitation créé par la Terre
est identique au champ de gravitation créé par la Terre 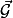 , soit
, soit 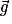 =
=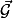 .
.Exercice n°1Exercice n°2Exercice n°3Exercice n°4
À savoir et savoir faire :
- Interpréter des expériences mettant en jeu l'interaction électrostatique et l'influence électrostatique.
- Connaître et utiliser la loi de Coulomb.
- Citer les analogies entre la loi de Coulomb et la loi d'interaction gravitationnelle.
- Connaître les expressions de la force de gravitation et du champ de gravitation.
- Connaître les expressions de la force électrostatique et du champ électrostatique.
- Savoir utiliser les expressions vectorielles de la force de gravitation et du champ de gravitation, de la force électrostatique et du champ électrostatique.
- Caractériser localement une ligne de champ électrostatique ou de champ de gravitation.
© 2000-2025, Miscellane