Les équations des réactions permettent de modéliser une transformation chimique, et ainsi de prévoir la composition finale du système. Elles permettent également de déterminer une quantité de matière initiale en connaissant la composition finale du système. Ainsi on pourra effectuer des titrages dans le domaine de la santé (pour effectuer des analyses sanguines, établir un diagnostic) et de l'environnement (pour quantifier un polluant), ainsi que pour le contrôle qualité des produits d'usage courant (aliments, boissons, produits ménagers ou pharmaceutiques), afin de garantir au consommateur un produit conforme.
I. Qu'est-ce qu'un dosage ? Un titrage ?
• Définition :
- Lorsque l'on cherche à déterminer la concentration ou la quantité de matière d'une espèce en solution, on réalise un dosage.
- La technique utilisée pour déterminer la concentration ou la quantité de matière d'une espèce en solution est le titrage.
• Lors du titrage, un volume précis (prise d'essai) de la solution titrée (espèce à doser) est placé dans un bécher, puis on ajoute progressivement la solution titrante de concentration connue placée dans la burette. La réaction chimique se produisant entre les espèces titrante et titrée est appelée réaction support du titrage.
• Exemple : Lors d'un dosage par titrage colorimétrique, la réaction de titrage se caractérise par un changement de couleur.
Exercice n°1
Exercice n°1
II. Quelle est la réaction support ?
• La réaction support est la réaction chimique qui se produit entre l'espèce titrée et l'espèce titrante.
• La réaction chimique utilisée est choisie de telle sorte que :
- la réaction soit totale : le réactif limitant doit être entièrement consommé ;
- la réaction soit rapide ;
- la réaction soit unique : les réactifs ne doivent pas intervenir dans une autre réaction.
• L'espèce dont on veut déterminer la concentration ou la quantité de matière intervient dans la réaction chimique.
Exercice n°2
Exercice n°2
III. Qu'est-ce que l'équivalence ?
• Définition : l'équivalence d'un titrage correspond à l'état final du système chimique pour lequel les réactifs (espèces titrée et titrante) ont été introduits en proportions stœchiométriques et sont donc entièrement consommés. Le volume total de solution titrante versée pour atteindre l'équivalence est appelé volume équivalent VE.
• Si l'une des espèces intervenant dans la réaction support du titrage est colorée, l'équivalence peut être visualisée par disparition d'une coloration ou apparition d'une coloration persistante : on parle de dosage colorimétrique. Si toutes les espèces sont incolores, il est possible de repérer l'équivalence à l'aide d'un indicateur coloré.
Exercice n°3
Exercice n°3
IV. Quelle est l'évolution du système lors d'un dosage par titrage colorimétrique ?
Quelle est l'évolution de la couleur du système ?
• On ajoute progressivement une solution d'ions permanganate (solution titrante) à une solution d'ions fer (II) (solution titrée) en milieu acide. Le volume initialement prélevé de solution d'ions fer (II) est noté : 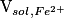 . La réaction a pour équation-bilan :
. La réaction a pour équation-bilan :
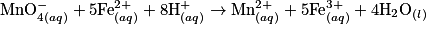 .
.
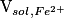 . La réaction a pour équation-bilan :
. La réaction a pour équation-bilan :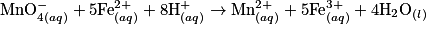 .
.• On suit l'évolution de la couleur de la solution, au fur et à mesure de l'ajout d'ions permanganate :
| Avant l'équivalence | À l'équivalence | Après l'équivalence |
|---|---|---|
| La solution passe progressivement du vert très pâle (la couleur des ions Fe2+) au jaune (la couleur des ions Fe 3+). Les ions fer (II) Fe2+ sont en excès par rapport aux ions permanganate 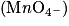 .Les ions permanganate sont le réactif limitant. .Les ions permanganate sont le réactif limitant. | La solution est jaune pâle. Il n'y a plus d'ions fer (II) ni d'ions permanganate. | La solution prend une teinte violette persistante (la couleur des ions permanganate, les ions manganèse Mn2+ étant incolores). Les ions permanganate sont en excès et les ions fer (II) sont le réactif limitant. |
• Par conséquent, avant l'équivalence le réactif limitant est l'espèce titrante et après l'équivalence il y a changement de réactif limitant puisque ce sera l'espèce titrée.
• L'équivalence est atteinte lorsque la goutte versée de permanganate modifie la couleur de la solution. De manière générale, lors des dosages par titrage colorimétrique, on pourra déterminer l'équivalence :
- par la disparition de la couleur initiale de l'espèce titrée due à sa consommation totale ;
- par l'apparition d'une coloration due à la présence de l'espèce titrante dans la solution.
• On lira directement sur la burette graduée le volume versé de solution titrante. Dans la suite, il sera noté : Véq.
Quelle est l'évolution de la composition du système ?
• La transformation chimique a pour équation : 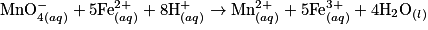 .
.
Les ions hydrogène sont en excès et l'eau est le solvant : les ions hydrogène et l'eau n'influencent pas la composition du système final. La réaction est totale.
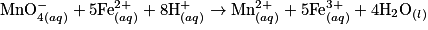 .
.Les ions hydrogène sont en excès et l'eau est le solvant : les ions hydrogène et l'eau n'influencent pas la composition du système final. La réaction est totale.
• Le tableau d'avancement est :
| Toutes les quantités en mol | Avancement | 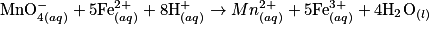 | |||||
| État initial | x = 0,0 | 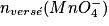 | 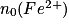 | Excès | 0,0 | 0,0 | Solvant |
| En cours de transformation | x | 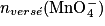 − x − x | 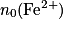 − 5x − 5x | Excès | x | 5 x | Solvant |
• Avant l'équivalence, les ions permanganate constituent le réactif limitant xmax = 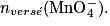
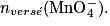
• À l'équivalence, les ions fer (II) et permanganate sont dans les proportions stœchiométriques :
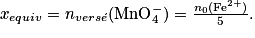
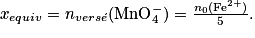
• Après l'équivalence, les ions fer (II) constituent le réactif limitant 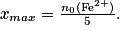
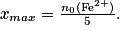
• Par conséquent, l'équivalence est obtenue pour le volume versé de solution titrante pour lequel les réactifs sont en proportions stœchiométriques.Exercice n°4
Quelle relation a-t-on à l'équivalence ?
• La concentration des ions permanganate est connue avec précision : c'est le réactif titrant. Elle sera notée ![[MnO_{4}^{-}]](https://static1.assistancescolaire.com/1/images/1_ph_03_m13.png) . La réaction chimique précédente permet de déterminer la quantité de matière, inconnue, des ions fer (II). L'équivalence est repérée par la persistance de la teinte violette à la goutte près. La lecture directe du volume versé de permanganate se fait sur les graduations de la burette. Ce volume à l'équivalence est Véq.
. La réaction chimique précédente permet de déterminer la quantité de matière, inconnue, des ions fer (II). L'équivalence est repérée par la persistance de la teinte violette à la goutte près. La lecture directe du volume versé de permanganate se fait sur les graduations de la burette. Ce volume à l'équivalence est Véq.
![[MnO_{4}^{-}]](https://static1.assistancescolaire.com/1/images/1_ph_03_m13.png) . La réaction chimique précédente permet de déterminer la quantité de matière, inconnue, des ions fer (II). L'équivalence est repérée par la persistance de la teinte violette à la goutte près. La lecture directe du volume versé de permanganate se fait sur les graduations de la burette. Ce volume à l'équivalence est Véq.
. La réaction chimique précédente permet de déterminer la quantité de matière, inconnue, des ions fer (II). L'équivalence est repérée par la persistance de la teinte violette à la goutte près. La lecture directe du volume versé de permanganate se fait sur les graduations de la burette. Ce volume à l'équivalence est Véq.• On sait qu'à l'équivalence, les ions fer (II) et permanganate sont dans les proportions stœchiométriques :
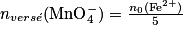
soit :
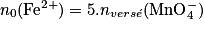 .
.
Comme la quantité de matière d'ions permanganate versés à l'équivalence est :
nversé![(\mathrm{MnO}_{4}^{-}) = [\mathrm{MnO}_{4}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m16.png) ,
,
à l'équivalence, on a :
![n_{0}(Fe^{2+}) = 5.[\mathrm{MnO}_{4}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}.](https://static1.assistancescolaire.com/1/images/1_ph_03_m17.png)
On peut également chercher la concentration de la solution d'ions fer (II). Comme le volume initialement prélevé de solution d'ions fer (II) est Vsol,Fe2+, on aura :
![n_{0}(\mathrm{Fe}^{2+}) = [\mathrm{Fe}^{2+}] \times \mathrm{V}_{\mathrm{sol,Fe}^{2+}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m18.png)
soit avec la relation obtenue à l'équivalence :
![[\mathrm{Fe}^{2+}] \times \mathrm{V}_{\mathrm{sol,Fe}^{2+}} = 5.[\mathrm{MnO}_{4}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m19.png) .
.
On isole à présent la concentration en ions fer (II) :
![[\mathrm{Fe}^{2+}] = \frac{5.[\mathrm{MnO}_{4}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}}{\mathrm{V}_{\mathrm{sol,Fe}^{2+}}}.](https://static1.assistancescolaire.com/1/images/1_ph_03_m20.png)
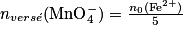
soit :
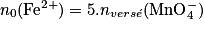 .
.Comme la quantité de matière d'ions permanganate versés à l'équivalence est :
nversé
![(\mathrm{MnO}_{4}^{-}) = [\mathrm{MnO}_{4}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m16.png) ,
,à l'équivalence, on a :
![n_{0}(Fe^{2+}) = 5.[\mathrm{MnO}_{4}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}.](https://static1.assistancescolaire.com/1/images/1_ph_03_m17.png)
On peut également chercher la concentration de la solution d'ions fer (II). Comme le volume initialement prélevé de solution d'ions fer (II) est Vsol,Fe2+, on aura :
![n_{0}(\mathrm{Fe}^{2+}) = [\mathrm{Fe}^{2+}] \times \mathrm{V}_{\mathrm{sol,Fe}^{2+}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m18.png)
soit avec la relation obtenue à l'équivalence :
![[\mathrm{Fe}^{2+}] \times \mathrm{V}_{\mathrm{sol,Fe}^{2+}} = 5.[\mathrm{MnO}_{4}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m19.png) .
.On isole à présent la concentration en ions fer (II) :
![[\mathrm{Fe}^{2+}] = \frac{5.[\mathrm{MnO}_{4}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}}{\mathrm{V}_{\mathrm{sol,Fe}^{2+}}}.](https://static1.assistancescolaire.com/1/images/1_ph_03_m20.png)
• Ainsi, le dosage réalisé permet de déterminer la quantité de matière ou la concentration en ions fer (II), c'est-à-dire de déterminer la quantité de matière ou la concentration de la solution titrée.
Exercice n°5
Exercice n°5
À savoir et savoir réaliser :
- Savoir définir ce qu'est un titrage avec suivi colorimétrique.
- Savoir déterminer les réactions d'oxydoréduction support du titrage.
- Relier qualitativement l'évolution des quantités de matière de réactifs et de produits à l'état final au volume de solution titrante ajoutée.
- Relier l'équivalence au changement de réactif limitant et à l'introduction des réactifs en proportions stœchiométriques.
- Connaître la définition de l'équivalence.
- Établir la relation entre les quantités de matière de réactifs introduites pour atteindre l'équivalence.
- Expliquer ou prévoir le changement de couleur observé à l'équivalence d'un titrage mettant en jeu une espèce colorée.
Exercice n°1
Qu'est-ce qu'un dosage ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
Doser une solution consiste à déterminer sa concentration. On peut utiliser différentes techniques : les titrages, les dosages par étalonnage…
Exercice n°2
Quelles propriétés doit avoir la réaction support d'un dosage ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
| ||
| ||
|
La réaction chimique utilisée est choisie de telle sorte qu'elle soit totale : le réactif limitant doit être entièrement consommé, qu'elle soit rapide : on ne doit pas attendre, et qu'elle soit unique : les réactifs ne doivent pas intervenir dans une autre réaction.
Exercice n°3
Lors d'un titrage, qu'est-ce que l'équivalence ?
Cochez la (ou les) bonne(s) réponse(s).
| ||
| ||
| ||
|
Par définition, l'équivalence d'un titrage correspond à l'état du système chimique pour lequel les réactifs (espèces titrée et titrante) ont été introduits en proportions stœchiométriques et sont donc entièrement consommés : il n'en reste plus en solution.
Exercice n°4
On réalise le dosage par titrage colorimétrique d'une solution de diiode 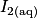 par une solution d'ions thiosulfate
par une solution d'ions thiosulfate 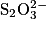 . Quelle est la relation entre les quantités de matière de réactifs titrant et titré à l'équivalence ?
. Quelle est la relation entre les quantités de matière de réactifs titrant et titré à l'équivalence ?
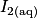 par une solution d'ions thiosulfate
par une solution d'ions thiosulfate 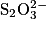 . Quelle est la relation entre les quantités de matière de réactifs titrant et titré à l'équivalence ?
. Quelle est la relation entre les quantités de matière de réactifs titrant et titré à l'équivalence ?Les couples oxydoréducteurs mis en jeu : 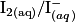 et
et 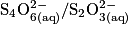 . La solution de diiode
. La solution de diiode 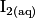 est colorée, elle est marron, et le
est colorée, elle est marron, et le 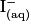 est jaune.
est jaune.
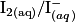 et
et 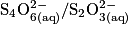 . La solution de diiode
. La solution de diiode 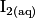 est colorée, elle est marron, et le
est colorée, elle est marron, et le 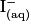 est jaune.
est jaune. Cochez la bonne réponse.
| ||
| ||
|
Écrivons les deux demi-équations d'oxydoréduction :
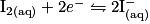
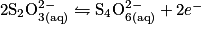
soit l'équation-bilan :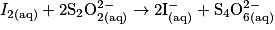 .
.
À l'équivalence, les réactifs sont introduits en proportions stœchiométriques. D'après l'équation de la réduction, on peut écrire à l'équivalence :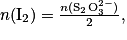
donc on aura :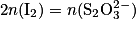 .
.
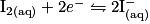
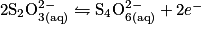
soit l'équation-bilan :
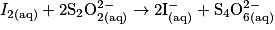 .
.À l'équivalence, les réactifs sont introduits en proportions stœchiométriques. D'après l'équation de la réduction, on peut écrire à l'équivalence :
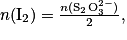
donc on aura :
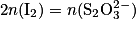 .
.Exercice n°5
On désire connaître la concentration en ions fer (II) d'une solution inconnue. Pour cela on réalise un dosage de la solution en ions fer (II) par une solution en ions nitrate NO3−(aq). L'équation support de la transformation est :
NO3−(aq) + 4 H+ + 3 Fe2+(aq) → 3 Fe3+(aq) + NO(g) + 2 H2O
Le protocole du dosage est le suivant : on prélève 10,0 mL de solution d'ions fer (II) et on dose par une solution d'ions nitrate de concentration![[\mathrm{NO3}] = 2,5 \times 10^{-2} \mathrm{mol} \cdot \mathrm{L}^{-1}](https://static1.assistancescolaire.com/1/images/1_ph_03_m35.png) .
.
L'équivalence du dosage est obtenue pour un volume versé Veq = 12,8 mL
Quelle est la concentration en ion fer (II) de la solution initiale ?
NO3−(aq) + 4 H+ + 3 Fe2+(aq) → 3 Fe3+(aq) + NO(g) + 2 H2O
Le protocole du dosage est le suivant : on prélève 10,0 mL de solution d'ions fer (II) et on dose par une solution d'ions nitrate de concentration
![[\mathrm{NO3}] = 2,5 \times 10^{-2} \mathrm{mol} \cdot \mathrm{L}^{-1}](https://static1.assistancescolaire.com/1/images/1_ph_03_m35.png) .
.L'équivalence du dosage est obtenue pour un volume versé Veq = 12,8 mL
Quelle est la concentration en ion fer (II) de la solution initiale ?
Cochez la bonne réponse.
| ||
| ||
| ||
|
D'après l'équation de la réaction, on peut écrire 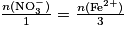 . Par conséquent, en isolant la quantité de fer (II), on obtient :
. Par conséquent, en isolant la quantité de fer (II), on obtient : 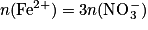 .
.
Or n = c × V où n est la quantité de matière, c la concentration de la solution et V le volume de la solution.
Par conséquent, en combinant les deux relations on arrive à :
![[\mathrm{Fe}^{2+}] \times \mathrm{V} = 3 \times [\mathrm{NO}_{2}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m42.png) ,
,
où V est le volume de la solution en ions fer (II) prélevée, [Fe2+] est la concentration en ion fer (II) et![[NO_{2}^{-}]](https://static1.assistancescolaire.com/1/images/1_ph_03_m43.png) est la concentration en ions nitrate,
est la concentration en ions nitrate,
soit :
![[Fe^{2+}] = \frac{3 \times [NO_{3}^{-}] \times \mathrm{V}_{\mathrm{eq}}}{\mathrm{V}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m44.png) .
.
Numériquement on a :
![[\mathrm{Fe}^{2+}] = \frac{3 \times 2,5\times 10^{-2}\times 12,8}{10,0} = 9,6.10^{-2} \,\mathrm{mol.L}^{-1}.](https://static1.assistancescolaire.com/1/images/1_ph_03_m45.png)
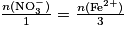 . Par conséquent, en isolant la quantité de fer (II), on obtient :
. Par conséquent, en isolant la quantité de fer (II), on obtient : 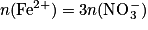 .
.Or n = c × V où n est la quantité de matière, c la concentration de la solution et V le volume de la solution.
Par conséquent, en combinant les deux relations on arrive à :
![[\mathrm{Fe}^{2+}] \times \mathrm{V} = 3 \times [\mathrm{NO}_{2}^{-}] \times \mathrm{V}_{\mathrm{\acute{e}q}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m42.png) ,
,où V est le volume de la solution en ions fer (II) prélevée, [Fe2+] est la concentration en ion fer (II) et
![[NO_{2}^{-}]](https://static1.assistancescolaire.com/1/images/1_ph_03_m43.png) est la concentration en ions nitrate,
est la concentration en ions nitrate,soit :
![[Fe^{2+}] = \frac{3 \times [NO_{3}^{-}] \times \mathrm{V}_{\mathrm{eq}}}{\mathrm{V}}](https://static1.assistancescolaire.com/1/images/1_ph_03_m44.png) .
.Numériquement on a :
![[\mathrm{Fe}^{2+}] = \frac{3 \times 2,5\times 10^{-2}\times 12,8}{10,0} = 9,6.10^{-2} \,\mathrm{mol.L}^{-1}.](https://static1.assistancescolaire.com/1/images/1_ph_03_m45.png)

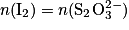
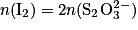
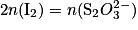
![[Fe^{2+}] = 1,1.10^{-2} \,\mathrm{mol}.\mathrm{L}^{-1}](https://static1.assistancescolaire.com/1/images/1_ph_03_m36.png)
![[Fe^{2+}] = 5,9.10^{-2} \,\mathrm{mol}.\mathrm{L}^{-1}](https://static1.assistancescolaire.com/1/images/1_ph_03_m37.png)
![[Fe^{2+}] = 9,6.10^{-2} \,\mathrm{mol}.\mathrm{L}^{-1}](https://static1.assistancescolaire.com/1/images/1_ph_03_m38.png)
![[Fe^{2+}] = 3,2.10^{-2} \,\mathrm{mol}.\mathrm{L}^{-1}](https://static1.assistancescolaire.com/1/images/1_ph_03_m39.png)

