Sujet 0, épreuve commune, exercice 3, 2019
Exercice 3 (5 points)
Une compagnie d'assurance auto propose deux types de contrat :
D'une manière générale, la probabilité d'un événement A est notée (A) et son événement contraire est noté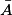 .
.
On note les événements suivants :
- un contrat « Tous risques » dont le montant annuel est 500 € ;
- un contrat « de base » dont le montant annuel est 400 €.
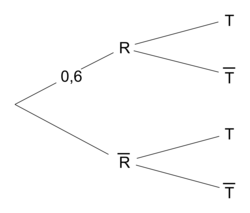
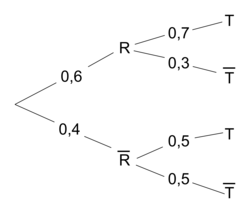
- 60 % des clients possèdent un véhicule récent (moins de 5 ans). Les autres clients ont un véhicule ancien ;
- parmi les clients possédant un véhicule récent, 70 % ont souscrit au contrat « Tous risques » ;
- parmi les clients possédant un véhicule ancien, 50 % ont souscrit au contrat « Tous risques ».
D'une manière générale, la probabilité d'un événement A est notée (A) et son événement contraire est noté
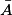 .
.On note les événements suivants :
- R « le client possède un véhicule récent » ;
- T « le client a souscrit au contrat "Tous risques" ».
1. Recopier et compléter l'arbre pondéré de probabilité traduisant les données de l'exercice.
 |
2. Calculer la probabilité qu'un client pris au hasard possède un véhicule récent et ait souscrit au contrat « Tous risques », c'est-à-dire calculer (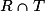 ).
).
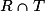 ).
).3. Montrer que (T) = 0,62.
4. La variable aléatoire X ne prend que deux valeurs a et b. Déterminer ces deux valeurs, les probabilités (X = a) et (X = b), puis l'espérance de X.
Annexes
© 2000-2025, Miscellane
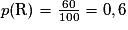 .
.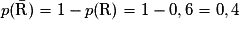 .
.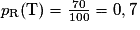 et
et 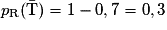 .
.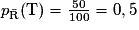 et
et 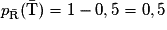 .
.
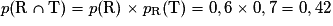
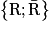 est une partition de l'univers Ω. En effet,
est une partition de l'univers Ω. En effet, 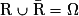 et
et 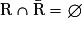 .
.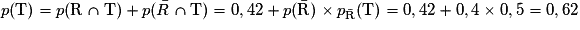 .
.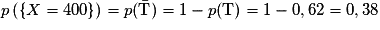 .
.