Probabilités : conditionnement
Fiche
Les probabilités conditionnelles prennent en compte les informations concernant l'issue d'une expérience qui modifient la probabilité des événements liés à cette expérience. On parle de probabilités conditionnelles lorsque deux événements d'une expérience aléatoire se réalisent l'un après l'autre, on regarde alors l'influence du premier sur le second.
1. Comment calculer une probabilité conditionnelle ?
Lecture d'un arbre
On considère une expérience aléatoire et deux événements A et B quelconques de probabilités non nulles. L'événement A est réalisé puis l'événement B.On peut visualiser la situation en utilisant un arbre pondéré :
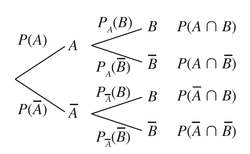 |
La probabilité de l'événement « B sachant que l'événement A est réalisé », notée PA (B) peut se calculer en utilisant un arbre.
En effet on a :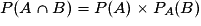 donc
donc 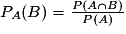 .
.
Par analogie on en déduit que la probabilité de l'événement « A sachant que l'événement B est réalisé », notée PB (A) sera égale à :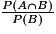 .
.
Exercice n°1
En effet on a :
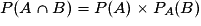 donc
donc 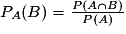 .
.Par analogie on en déduit que la probabilité de l'événement « A sachant que l'événement B est réalisé », notée PB (A) sera égale à :
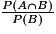 .
.Exercice n°1
2. Comment montrer que deux événements sont indépendants ?
Propriété
Intuitivement, deux événements sont indépendants si la réalisation de l'un de ces événements n'influe pas sur la probabilité de l'autre. On doit donc avoir : PA(B) = P(B).A et B sont donc indépendants si et seulement si
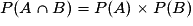 .
.Remarque
Attention à ne pas confondre incompatibles et indépendants :- A et B sont donc incompatibles si et seulement si
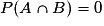 ;
; - A et B sont donc indépendants si et seulement si
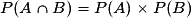 .
.
3. Comment utiliser la formule des probabilités totales ?
4. Comment estimer la valeur de π grâce aux probabilités ?
Algorithme : Approximation de Pi par la méthode de Monte-Carlo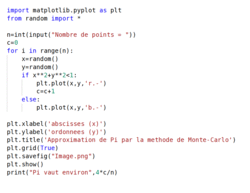 |
En choisissant mille points (n=1000) on obtient par exemple ceci :
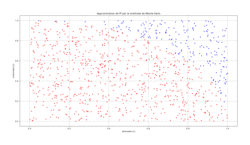 |
À retenir
- La probabilité de l'événement « B sachant que l'événement A est réalisé » (avec
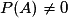 ) est
) est 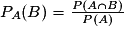 .
. - A et B sont indépendants si et seulement si
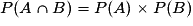 .
. 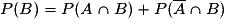 .
.
© 2000-2025, Miscellane
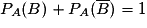 .
.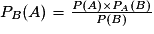 .
.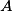 et
et 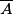 .
.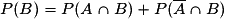 .
.