La fonction exponentielle

Fiche

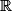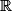C'est en recherchant des fonctions dérivables sur $\mathbb{R}$ dont la dérivée est proportionnelle à la fonction que l'on est conduit à l'étude de la fonction exponentielle. Celle-ci joue un rôle capital en mathématiques, car c'est une fonction de référence : elle intervient dans de nombreuses lois de probabilité.

1. Comment définir la fonction exponentielle ?

Définition

La fonction exponentielle est l'unique fonction dérivable sur l'ensemble des réels vérifiant les deux conditions suivantes :

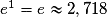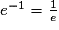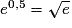pour tout réel x, exp'(x) = exp(x) et exp(0) = 1. Conséquences : e⁰ = 1 ; $e^{1}=e\approx {2,718}$ ; $e^{-1}=\frac{1}{e}$ et $e^{0,5}=\sqrt{e}$ ;
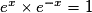pour tout réel x on a : $e^{x}\times e^{-x}=1$ .

Dérivée, courbe représentative

La fonction exponentielle est égale à sa dérivée.
La fonction exponentielle est strictement positive sur 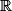$\mathbb{R}$ , donc sa fonction dérivée aussi, ainsi la fonction exponentielle est strictement croissante sur Ensemble R

Courbe représentative de la fonction exponentielle

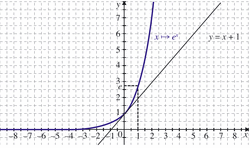Dérivée de la fonction e^u

Soit u une fonction dérivable sur un intervalle I, alors pour tout réel x appartenant à I on a : (e^u)'(x) = u'(x)×e^u(x).
Exercice n°1 Exercice n°2

2. Quelles sont les propriétés à retenir ?

Propriétés :

relation fonctionnelle : quels que soient les réels x et y on a : e^x × e^y = e^x+y ;
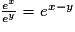quels que soient les réels x et y on a $\frac{e^{x}}{e^{y}}=e^{x-y}$ ;
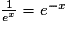pour tout nombre réel x on a : $\frac{1}{e^{x}}=e^{-x}$ ;
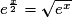pour tout nombre réel x on a : $e^{\frac{x}{2}}=\sqrt{e^{x}}$ ;
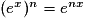pour tout nombre réel x et pour tout entier n on a : $(e^{x})^{n}=e^{nx}$ ;
e^a = e^b si et seulement si a = b ;
e^a <e^b si et seulement si a<b.

Exercice n°4 Exercice n°5 Exercice n°6

À retenir

La fonction exponentielle est l'unique fonction f dérivable sur l'ensemble des réels qui est sa propre dérivée et qui vérifie f(0) = 1.
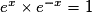Pour tout réel x on a : $e^{x}\times e^{-x}=1$ .
Soit u une fonction dérivable sur un intervalle I, alors pour tout réel x appartenant à I on a : (e^u)'(x) = u'(x)×e^u(x).
Exp(x) > 0 pour tout réel x.