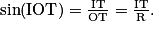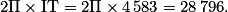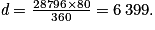Sujet zéro, épreuve commune, sujet 1, la sphéricité de la Terre, 2020

Énoncé

L'usage d'une calculatrice est autorisé.

Les Grecs de l'Antiquité attribuaient déjà à la Terre une forme sphérique et Ératosthène (276-194 av. JC) fut le premier à en calculer la circonférence. Dans tout ce qui suit, la Terre est assimilée à une sphère de rayon 6 371 km.

Partie 1. Repérage sur la sphère terrestre

Afin de se repérer à la surface de la sphère terrestre, on utilise des coordonnées géographiques (longitude, latitude).

Ville	Pays	Longitude	Latitude
Libreville	Gabon	9° Est	0°
Quito	Équateur	79° Ouest	0°
Toronto	Canada	79° Ouest	44° Nord
Toulouse	France	1° Est	44° Nord

Questions :

1. Calculer la longueur d'un méridien terrestre.

Le méridien est un cercle imaginaire passant par les pôles géographiques.

2. À partir des informations du tableau ci-dessus :

2. 1. Indiquer les villes qui sont situées sur un même méridien.

Le méridien passe par les pôles. Les villes situées sur un même méridien se trouvent sur cette même ligne imaginaire.

2. 2. Indiquer les villes qui sont situées sur un même parallèle.

Un parallèle est une ligne imaginaire qui est parallèle à l'équateur.

3. On note O le centre de la Terre et T, Q et T' les villes Toronto, Quito et Toulouse. On note I le centre du parallèle passant par Toronto et Toulouse. Sur le schéma ci-dessous (figure 1a.) représentant la sphère terrestre, on a placé les points O, I, Q, T et T'.

Document 1. Représentations graphiques permettant un repérage spatial sur la sphère.

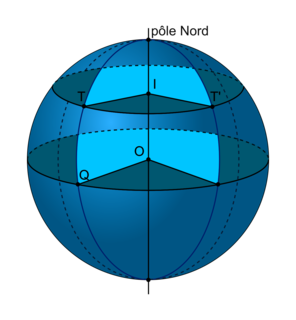Figure 1a. Sphère terrestre

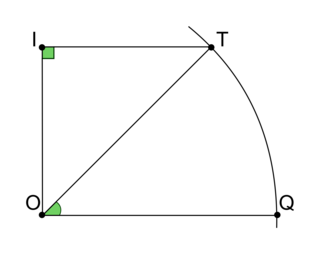Figure 1b. Plan contenant l'axe des pôles et le point T

3. 1. Donner la mesure, en degrés, des angles QOT et TIT'.

Quito se trouve sur l'équateur et T et T' sont sur la même ligne.

3. 2. Calculer la longueur de la portion de méridien reliant Quito à Toronto.

Faire un tableau de proportionnalité entre la longueur d'un méridien et l'angle QOT.

4. À l'aide de la figure 1b :

4. 1. Préciser la longueur OT puis calculer la longueur IT.

O est le centre de la Terre et T représente une ville à la surface. L'angle QOI est un angle droit et le triangle TIO est rectangle en I.

4. 2. En déduire la longueur du parallèle passant par Toulouse et Toronto.

La longueur du parallèle correspond au périmètre du cercle passant par Toulouse et Toronto.

4. 3. Justifier, par un calcul, que la longueur de la portion de parallèle reliant Toulouse à Toronto est environ égale à 6 399 km.

Il faut utiliser le même raisonnement que pour calculer la longueur de la portion de méridien reliant Quito à Toronto. Ici, en revanche, le rayon n'a pas la même valeur.

5. Un système d'information géographique (SIG) donne les informations suivantes :

• distance Quito-Toronto : 4 891 km ;

• distance Toulouse-Toronto : 6 230 km.

Pour un système d'information géographique, la distance entre deux points du globe est le plus court chemin qui les relie à la surface de la Terre.
Expliquer pourquoi les longueurs données par le SIG et celles calculées dans les questions 3 et 4 sont, dans un cas, très proches alors que, dans l'autre, elles ne le sont pas.

Le plus court chemin entre deux points sur une sphère correspond à l'arc du grand cercle (qui est un cercle dont le centre est le même que celui de la sphère). L'équateur est un grand cercle et les méridiens sont des demi-grands cercles.

Partie 2 : Les différents climats de la Terre

Document 2. Les zones climatiques à la surface de la Terre.

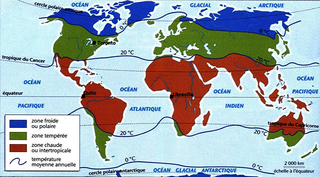Sur cette carte, on constate que Quito et Libreville, qui sont à la même latitude, sont dans une zone chaude intertropicale. À Toronto, situé à la même longitude que Quito, la température moyenne annuelle est plus froide.
Afin d'expliquer ces différences climatiques, un élève a proposé comme hypothèse :
« Il fait plus chaud à l'équateur qu'aux pôles parce que La Terre est plus proche du Soleil à l'équateur qu'aux pôles ».

6. À partir des connaissances acquises et des informations issues des documents 3 et 4, rédiger un paragraphe argumenté permettant à la fois d'expliquer qu'il fait plus chaud à l'équateur qu'aux pôles et d'invalider l'hypothèse émise par cet élève.
La justification des arguments pourra s'appuyer sur des schémas explicatifs.

Déterminer une problématique, décrire les documents proposés et analyser ces documents par rapport à la problématique, puis y répondre.

Document 3. Puissance solaire en fonction de la distance au Soleil (en unités astronomiques u.a., 1 u.a. = 1,5 × 10⁸ km).

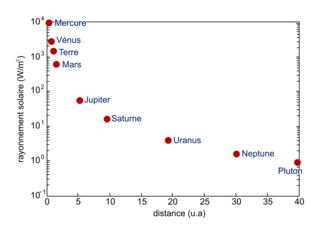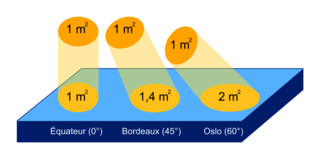
Document 4. Puissance solaire reçue par unité de surface en fonction de la latitude.

Résultats observés pour un même éclairage de l'équateur (en haut) et des pôles (en bas).
Tableau 1. Correspondance entre la latitude et l'énergie solaire reçue par unité de surface.

Latitude	0°	45° Nord	60° Nord	89° Nord
Pays, régions, villes correspondant à la latitude	Équateur, Brésil, Kenya	Bordeaux	Oslo, Saint Pétersbourg	Pôle Nord
Surface recevant une même quantité d'énergie (m²)	1	1,4	2	57
Puissance solaire reçue en moyenne par unité de surface (W/m²)	420	420 × 1 / 1,4 = 300	420 × 1 / 2 = 210	420 × 1 / 57 = 7,36

Corrigé

1. Comme on assimile la Terre à une sphère, le méridien sera un cercle du rayon de celui de la Terre. Soit d'une longueur en km de : $\textrm{L} = 2\Pi \times \textrm{R}= 2\Pi \times 6 371 = 40\,030$ .

2. 1. Pour se situer sur le même méridien, il faut être à la même longitude. On voit donc que les villes de Quito et Toronto sont sur le même méridien.

2. 2. Pour se situer sur le même parallèle, il faut être à la même latitude. On voit donc que les villes de Toronto et Toulouse sont sur le même parallèle. De même, Libreville et Quito sont sur le même parallèle.

3. 1. Par définition de la latitude, qui correspond à l'angle entre un point de la Terre et l'équateur, l'angle QOT est égal à 44°.
Comme Toronto et Toulouse sont sur le même parallèle, l'angle TIT' = 79° + 1° = 80°.

3. 2. Un cercle en entier est associé à un angle de 360°, et correspond à la longueur du méridien qui est de 40 030 km. Or l'angle QOT = 44°.

Angle en °	360	44
Distance en km	40 030

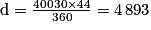Le calcul qui donne la distance en km entre T et Q est : $\textrm{d} = \frac{40 030 \times 44}{360} = 4\,893$ .

4. 1. Comme la distance OT correspond au rayon de la Terre : OT = 6 371 km.
Or l'angle IOT = 90° − 44° = 46°,
et dans le triangle TIO, on a $\textrm{sin}(\textrm{IOT}) = \frac{\textrm{IT}}{\textrm{OT}} = \frac{\textrm{IT}}{\textrm{R}}.$
d'où IT(en km = R × sin(IOT) = 6 371 × sin(46) = 4 583.

4. 2. Le cercle passant par Toulouse et Toronto est associé à un angle de 360° et a un rayon IT = 4 583 km. Le périmètre de ce cercle en km est donc $2\Pi \times \textrm{IT} = 2\Pi \times 4\,583 = 28\,796.$

4. 3. L'angle entre Toronto et Toulouse, d'après les questions précédentes, vaut 80°.
D'où :

Angle en °	360	80
Distance en km	28 796

Le calcul qui donne la distance en km entre Toronto et Toulouse est : $\textit{d} = \frac{28 796 \times 80}{360} = 6\,399.$

5. La distance Toronto-Quito calculée (4 893 km) est proche de la distance donnée par le SIG (4 891 km). Mais la distance Toronto-Toulouse calculée (6 399 km) est très différente de la distance donnée par le SIG (6 230 km).
En effet le plus court chemin à la surface d'une sphère est la distance reliant ces deux points sur un grand cercle. Un grand cercle a le même centre que le centre de la Terre. Comme Toronto et Quito sont sur le même méridien, ils sont sur un grand cercle. Par contre la distance de Toulouse à Toronto, situé sur le même parallèle, n'a pas été calculée avec le grand cercle : ce n'est donc pas la plus courte distance entre les deux villes.

6. Construction du paragraphe argumenté :
Comment expliquer que le climat d'une ville située sur l'équateur soit plus chaud que celui d'une ville plus près du pôle Nord, à longitude identique ?
Analyse des documents
Le document 3 montre que la distance entre la Terre et le Soleil est très grande (1,5 × 10⁸ km), comparée aux distances sur Terre. On peut donc considérer que tous les points sur Terre sont à la même distance du Soleil.
Le document 4 montre que la puissance solaire reçue du Soleil sur une surface de 1 m² dépend en revanche de la latitude. La puissance solaire reçue dépend donc de l'angle entre la normale à la surface et la direction du Soleil. En effet, à l'équateur (latitude 0°), les rayons solaires sont perpendiculaires au sol.
Explication
La surface recevant une même quantité d'énergie est minimale à l'équateur et maximale au pôle Nord. L'énergie est plus importante à l'équateur : il y fait plus chaud. L'énergie est plus diffuse au pôle Nord : il y fait moins chaud.
En effet, plus l'inclinaison des rayons solaires est grande, plus la surface balayée par la même quantité d'énergie est grande.
Or, la même quantité d'énergie se répartit sur une surface plus grande : elle est donc plus faible si on la ramène à 1 m². Ainsi le rayonnement est maximum à l'Équateur.

Réponse à la problématique
La distance entre le Soleil et la Terre est très grande par rapport à la circonférence de la Terre : la distance du pôle Nord au Soleil peut donc être considérée comme la même que la distance de l'équateur au Soleil. L'hypothèse de l'élève est donc invalidée.
Pourtant, c'est bien la latitude qui permet d'expliquer la puissance solaire reçue. Quito et Libreville sont à la même latitude et sur l'équateur : ces villes ont donc un climat similaire et chaud. Toronto et Quito sont sur la même longitude, mais Toronto est sur la latitude 44°. Comme la ville de Toronto est plus proche du pôle Nord que Quito qui se trouve sur l'équateur, elle aura un climat plus froid.