Phénomènes d'évolution : nombre dérivé
Fiche
I. Qu'est-ce qu'une tangente à une courbe ?
• Si l'on considère une courbe représentative d'une fonction et que l'on zoome très fortement sur un point de la courbe, alors on peut remarquer que localement autour du point la courbe a l'apparence d'une droite.
• Définition : Soit une fonction f définie sur un intervalle I. Soit a un réel de I. On munit le plan d'un repère et on note Cf la courbe représentative de f. Soit A le point de Cf d'abscisse a. Soit M un point de Cf distinct de A. La droite (AM) est sécante à la courbe Cf : elle coupe Cf en deux points (A et M).
• Lorsque l'on approche le plus possible le point M du point A, alors la position limite des sécantes passant par A est la tangente à Cf (si elle existe) au point A.
Illustration :
Illustration :
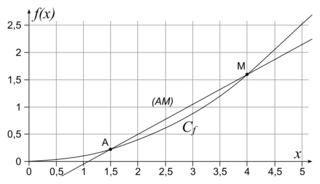 |
• (AM) est sécante à Cf.
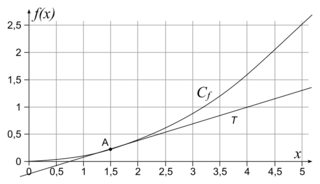
• M est aussi proche de A (sans être confondu avec A) que possible, la droite « frôle » la courbe Cf et admet localement un unique point de contact : A. Elle est la position limite des sécantes : c'est la tangente T.
 |
II. Qu'est-ce que le nombre dérivé d'une fonction en un réel ?
• Définition : Soit une fonction f définie sur un intervalle I. Soit a un réel de I. On munit le plan d'un repère et on note Cf la courbe représentative de f. Si Cf admet une unique tangente T (non verticale) au point A d'abscisse a, alors on dit que le nombre dérivé de f en a est égal au coefficient directeur de la tangente T.
• Exemple :
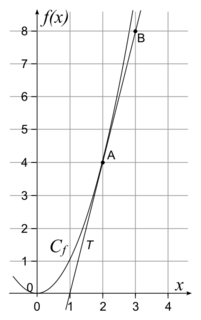 |
• On considère la fonction carré qui, à un réel x, lui associe son carré x2. On la note f.
• On considère le point A d'abscisse 2 appartenant à Cf. On a donc A(2 ; f(2)) soit A(2 ; 22) ou A(2 ; 4).
• On a tracé T la tangente à Cf au point A.
• On nous donne le point B(3 ; 8) qui appartient à T.
• La droite (AB) est donc la tangente T.
• Pour calculer le coefficient directeur de (AB), on utilise la formule suivante :
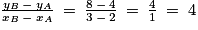
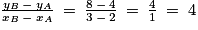
• Donc le coefficient directeur de T est égal à 4.
• Ainsi on dira que le nombre dérivé de la fonction carré en 2 est égal à 4.Exercice n°1
• Notation : Si le nombre dérivé d'une fonction f en un réel a existe, alors il est noté 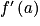 .
.
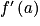 .
.III. Comment interpréter le nombre dérivé dans l'étude de l'évolution d'un phénomène ?
• Lorsqu'une fonction est croissante sur un intervalle, on peut être amené à vouloir quantifier sa croissance, c'est-à-dire à déterminer sa vitesse de croissance.
• Si une fonction croissante f modélise l'évolution d'une grandeur selon le temps, alors le nombre dérivé de f en a (quand il existe) représente la vitesse d'évolution à l'instant a (vitesse instantanée).
• Si une fonction décroissante f modélise l'évolution d'une grandeur selon le temps, alors l'opposé du nombre dérivé de f en a (quand il existe) représente la vitesse d'évolution à l'instant a (vitesse instantanée).
• Exemple : On lâche une balle en plastique du haut d'un immeuble d'une hauteur de 200 mètres (sans personne en dessous). On considère la fonction d qui à x secondes écoulées depuis le lâcher de la balle associe la distance parcourue (en mètres) par la balle. D'après un physicien, on peut admettre que pour tout x de [0 ; 10] : d(x) = 4,9x2.
• On obtient la représentation graphique suivante à l'aide du logiciel de géométrie dynamique.
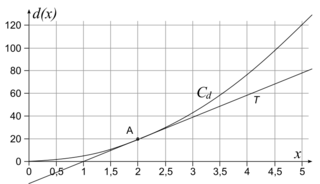 |
• La tangente T à Cd au point A d'abscisse 2 a été tracée. On va pouvoir déterminer le nombre dérivé de d en 2.
Cherchons l'ordonnée de A. A(2 ; d(2)), car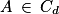 . d(2) = 4,9 × 22 = 19,6. Ainsi A(2 ; 19,6).
. d(2) = 4,9 × 22 = 19,6. Ainsi A(2 ; 19,6).
La tangente semble couper l'axe des abscisses en B(1 ; 0).
La droite (AB) est donc la tangente T.
Calculons le coefficient directeur de (AB) :
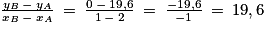
Donc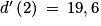 .
.
Cherchons l'ordonnée de A. A(2 ; d(2)), car
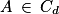 . d(2) = 4,9 × 22 = 19,6. Ainsi A(2 ; 19,6).
. d(2) = 4,9 × 22 = 19,6. Ainsi A(2 ; 19,6).La tangente semble couper l'axe des abscisses en B(1 ; 0).
La droite (AB) est donc la tangente T.
Calculons le coefficient directeur de (AB) :
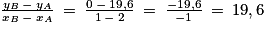
Donc
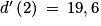 .
.• Cela signifie que 2 secondes après avoir lâché la balle, sa vitesse instantanée est de 19,6 m/s.
On peut d'ailleurs conjecturer graphiquement que cette vitesse va augmenter au fil du temps (jusqu'à l'impact a priori).
Exercice n°2
On peut d'ailleurs conjecturer graphiquement que cette vitesse va augmenter au fil du temps (jusqu'à l'impact a priori).
Exercice n°2
IV. Comment déterminer graphiquement l'équation réduite d'une tangente à une courbe ?
• Méthode : On va lire graphiquement les coordonnées de deux points appartenant à la tangente. Le premier point est souvent le point de contact local avec la courbe représentative de la fonction. Pour le second point, on peut essayer de privilégier le point d'intersection entre la courbe et l'axe des ordonnées, sinon on sélectionne un point dont on arrive à lire facilement les coordonnées (souvent entières).
• Propriété : L'équation réduite d'une tangente T à une courbe Cf au point d'abscisse a (non parallèle à l'axe des ordonnées) est l'unique égalité de la forme y = mx + p (avec m et p qui sont deux réels à déterminer), vérifiée par les coordonnées des points de T.
• Remarque : Le réel m est le nombre dérivé de la fonction f en a. C'est-à-dire 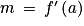 .
.
Le réel p est l'ordonnée à l'origine de T, c'est l'ordonnée du point d'intersection entre T et l'axe des ordonnées. On peut soit déterminer p graphiquement (lorsque cela est possible), soit par le calcul.
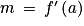 .
.Le réel p est l'ordonnée à l'origine de T, c'est l'ordonnée du point d'intersection entre T et l'axe des ordonnées. On peut soit déterminer p graphiquement (lorsque cela est possible), soit par le calcul.
• Exemple :
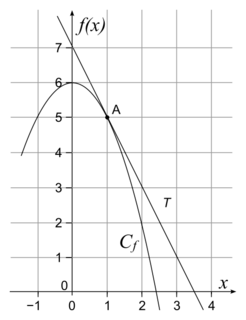 |
• Considérons la fonction f définie sur 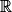 par f(x)= 6 – x2.
par f(x)= 6 – x2.
Soit A le point de Cf d'abscisse 1.
Soit T la tangente à Cf en A.
Déterminons graphiquement l'équation réduite de T.
On cherche donc m et p réels tels que :
T : y = mx + p
D'une part :
f(1) = 6 – 12 = 6 – 1 = 5
Donc A(1 ; 5).
D'autre part on lit que B(0 ; 7) appartient à T. C'est le point d'intersection entre T et l'axe des ordonnées donc p = 7.
Enfin on sait que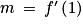 .
.
La droite (AB) est la droite T.
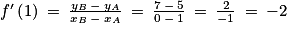
Ainsi :
T : y = 2x + 7
Exercice n°3
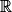 par f(x)= 6 – x2.
par f(x)= 6 – x2.Soit A le point de Cf d'abscisse 1.
Soit T la tangente à Cf en A.
Déterminons graphiquement l'équation réduite de T.
On cherche donc m et p réels tels que :
T : y = mx + p
D'une part :
f(1) = 6 – 12 = 6 – 1 = 5
Donc A(1 ; 5).
D'autre part on lit que B(0 ; 7) appartient à T. C'est le point d'intersection entre T et l'axe des ordonnées donc p = 7.
Enfin on sait que
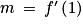 .
.La droite (AB) est la droite T.
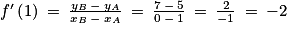
Ainsi :
T : y = 2x + 7
Exercice n°3
V. Comment déterminer algébriquement l'équation réduite d'une tangente à une courbe ?
• Propriété : l'équation réduite d'une tangente T à une courbe Cf au point d'abscisse a (non parallèle à l'axe des ordonnées) est l'égalité 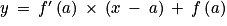 .
.
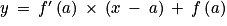 .
.• Exemple : Considérons la fonction d définie par d(x) = 4,9x2. On a montré précédemment que 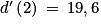 .
.
Déterminons l'équation réduite de la tangente T à la courbe Cd au point A d'abscisse 2.
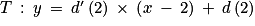
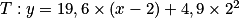
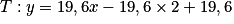
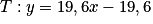
Exercice n°4
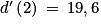 .
.Déterminons l'équation réduite de la tangente T à la courbe Cd au point A d'abscisse 2.
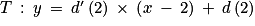
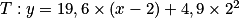
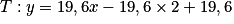
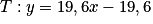
Exercice n°4
© 2000-2025, Miscellane