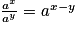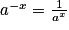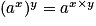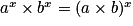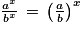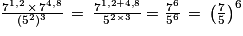Phénomènes d'évolution : fonctions exponentielles
Fiche
I. Qu'est-ce qu'une fonction exponentielle ?
• Introduction : Les suites géométriques sont de bons outils pour étudier des phénomènes discrets à croissance exponentielle (pour passer d'une valeur à la suivante, on multiplie toujours par un même nombre). On cherche à prolonger cet outil pour étudier des phénomènes continus.
• Par exemple, une population ne va pas doubler subitement entre deux dates, il serait donc intéressant d'observer l'évolution de cette population de manière plus fine.
• Définition : Soit a un réel strictement positif. Une fonction f définie pour tout réel x positif par f(x) = ax est appelée fonction exponentielle de base a.
• Calcul : On utilisera la calculatrice pour calculer les valeurs de ax avec a et x donnés à l'aide de la touche exposant : 

• Exemple : On considère qu'une certaine cellule se dédouble toutes les heures. On étudie un milieu contenant cent cellules.
On pose f la fonction qui à x heures écoulées depuis le début de l'expérience associe f(x) le nombre de cellules (en centaines) présentes dans le milieu.
On a donc pour tout x de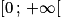 : f(x) = 1 × 2x = 2x.
: f(x) = 1 × 2x = 2x.
On peut, par exemple, déterminer le nombre de cellules présentes après 30 minutes.
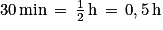 .
.
On calcule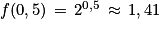 .
.
Ainsi il y a environ 141 cellules présentes dans le milieu au bout de 30 minutes.
Exercice n°1
On pose f la fonction qui à x heures écoulées depuis le début de l'expérience associe f(x) le nombre de cellules (en centaines) présentes dans le milieu.
On a donc pour tout x de
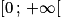 : f(x) = 1 × 2x = 2x.
: f(x) = 1 × 2x = 2x.On peut, par exemple, déterminer le nombre de cellules présentes après 30 minutes.
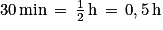 .
.On calcule
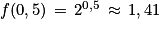 .
.Ainsi il y a environ 141 cellules présentes dans le milieu au bout de 30 minutes.
Exercice n°1
II. Quelles sont les propriétés algébriques des fonctions exponentielles ?
• Convention : Soit a un réel strictement positif.
a0 = 1
a0 = 1
• Propriété fondamentale :
- Soit a un réel strictement positif.
- Soit x et y deux réels strictement positifs.
- ax+y = ax × ay
• On dit que les fonctions exponentielles « transforment les sommes en produits ».
• Propriétés : On prolonge les propriétés déjà connues sur les puissances.
Soit a et b deux réels strictement positifs. Soit x et y deux réels strictement positifs.
Soit a et b deux réels strictement positifs. Soit x et y deux réels strictement positifs.
III. Comment étudier le sens de variation d'une fonction exponentielle ?
• Propriété 1 : Soit a un réel strictement positif.
Soit la fonction f exponentielle de base a définie pour tout réel x positif par f(x) = ax :
Soit la fonction f exponentielle de base a définie pour tout réel x positif par f(x) = ax :
- si a > 1, alors f est strictement croissante sur
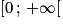 ;
; - si a = 1, alors f est constante sur
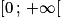 ;
; - si 0 < a < 1, alors f est strictement décroissante sur
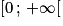 .
.
• Propriété 2 : Soit a un réel strictement positif. Soit k un réel. Soit f la fonction exponentielle de base a.
Soit la fonction g définie pour tout réel x positif par g(x) = k × ax :
Soit la fonction g définie pour tout réel x positif par g(x) = k × ax :
- si k > 0, alors g et f ont le même sens de variation ;
- si k < 0, alors g et f ont un sens de variation contraire.
• Exemple : Une entreprise fabrique du sable. Le bureau d'études estime que le côut journalier de production peut être modélisé par une fonction c qui à x tonnes de sable produites associe c(x) le coût journalier (en milliers d'euros) pour fabriquer x tonnes de sable.
Avec pour tout x de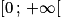 : c(x) = 1,8 × 1,04x.
: c(x) = 1,8 × 1,04x.
Étudions le sens de variation de la fonction c.
Soit f la fonction exponentielle de base a = 1,04. Comme a > 1, alors f est strictement croissante sur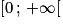 . De plus 1,8 > 0. Donc c et f ont le même sens de variation.
. De plus 1,8 > 0. Donc c et f ont le même sens de variation.
Ainsi la fonction c est strictement croissante sur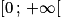 .
.
Cela signifie que plus l'entreprise fabrique de sable, plus le coût journalier de fabrication augmente.
Exercice n°3
Avec pour tout x de
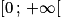 : c(x) = 1,8 × 1,04x.
: c(x) = 1,8 × 1,04x.Étudions le sens de variation de la fonction c.
Soit f la fonction exponentielle de base a = 1,04. Comme a > 1, alors f est strictement croissante sur
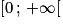 . De plus 1,8 > 0. Donc c et f ont le même sens de variation.
. De plus 1,8 > 0. Donc c et f ont le même sens de variation.Ainsi la fonction c est strictement croissante sur
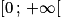 .
.Cela signifie que plus l'entreprise fabrique de sable, plus le coût journalier de fabrication augmente.
Exercice n°3
IV. À quoi ressemble la représentation graphique d'une fonction exponentielle ?
• Soit a un réel strictement positif. Soit la fonction f exponentielle de base a définie pour tout réel x positif par f(x) = ax.
Premier cas : 0 < a < 1.
La courbe représentative de f « descend » et vient « s'écraser » sur l'axe des abscisses. On parle de décroissance exponentielle.
Exemple 1 :
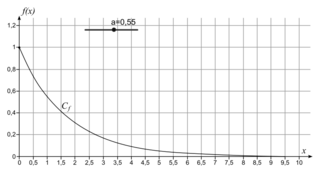
Premier cas : 0 < a < 1.
La courbe représentative de f « descend » et vient « s'écraser » sur l'axe des abscisses. On parle de décroissance exponentielle.
Exemple 1 :
 |
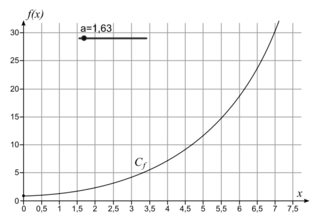
Second cas : a > 1.
La courbe représentative de f « monte » et « explose vers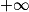 ». On dit que la croissance est exponentielle.
». On dit que la croissance est exponentielle.
La courbe représentative de f « monte » et « explose vers
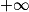 ». On dit que la croissance est exponentielle.
». On dit que la croissance est exponentielle.Exemple 2 :
 |
V. Qu'est-ce que la racine n-ième d'un réel positif ?
• Définition : Soit y un réel positif. Soit n un entier naturel non nul. On considère l'équation d'inconnue x suivante : xn = y
- Cette équation admet une unique solution réelle positive.
- On appelle cette solution racine nième du nombre y.
- On la note par exemple :
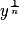
• Exemple : La racine 3-ième du nombre 8 est la solution positive de l'équation x3 = 8.
On cherche donc le réel positif qui élevé au cube est égal à 8. Ce réel est 2.
Ainsi :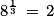
On cherche donc le réel positif qui élevé au cube est égal à 8. Ce réel est 2.
Ainsi :
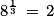
• Remarque : On utilise souvent la calculatrice pour trouver une valeur approchée de la racine n-ième d'un réel.
Par exemple, la racine 4-ième de 10 est égale à environ 1,7783.
On a tapé :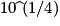
Exercice n°4
Par exemple, la racine 4-ième de 10 est égale à environ 1,7783.
On a tapé :
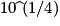
Exercice n°4
VI. Comment calculer un taux d'évolution moyen ?
Rappel :• Propriété : Soit n un entier naturel non nul. Supposons qu'après n périodes, le taux d'évolution global d'une grandeur est de T% (si l'évolution est une augmentation alors T > 0, si l'évolution est une diminution alors T < 0).
Alors le taux d'évolution moyen par période est égal à :
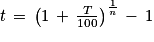
(t > 0 si T > 0 et t < 0 si T < 0)
Alors le taux d'évolution moyen par période est égal à :
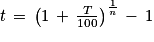
(t > 0 si T > 0 et t < 0 si T < 0)
• Exemple : La France a émis 407,8 MtCO2e de gaz à effet de serre (GES) en 2022.
L'objectif fixé par la Stratégie Nationale Bas Carbone (SNBC) pour 2030 est de 310 MtCO2e.
Il faudra donc une diminution globale d'environ 24 % des GES par la France entre 2022 et 2030.
Déterminons le taux de diminution moyen annuel que le gouvernement doit communiquer aux différentes administrations.
Déterminons d'abord le nombre de périodes (ici des années) entre 2030 et 2022 :
2030 − 2022 = 8
L'objectif fixé par la Stratégie Nationale Bas Carbone (SNBC) pour 2030 est de 310 MtCO2e.
Il faudra donc une diminution globale d'environ 24 % des GES par la France entre 2022 et 2030.
Déterminons le taux de diminution moyen annuel que le gouvernement doit communiquer aux différentes administrations.
Déterminons d'abord le nombre de périodes (ici des années) entre 2030 et 2022 :
2030 − 2022 = 8
• On peut maintenant calculer :
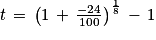
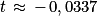
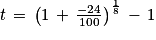
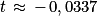
• Ainsi il faudra diminuer en moyenne de 3,37 % les GES en France entre 2022 et 2030 pour atteindre les objectifs du SNBC.
Source : https://www.observatoire-climat-energie.fr/climat/global/
Exercice n°5
Source : https://www.observatoire-climat-energie.fr/climat/global/
Exercice n°5
© 2000-2025, Miscellane