Soit une pyramide régulière de base carrée ABCD et de hauteur [SO].
On a
AB = 2 ;
SO = 7.
AB = 2 ;
SO = 7.
 |
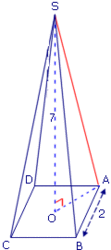On veut calculer SA.
[SA] est l'hypoténuse du triangle rectangle SOA, dont les deux autres côtés sont :
- la hauteur [SO],
- la demi-diagonale [OA] du carré ABCD.
• Il faut donc d'abord calculer la longueur de la demi-diagonale [OA].
AC = AB ×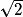
= 2
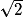
donc OA =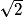
.
AC = AB ×
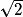= 2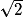donc OA =
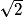.• On applique ensuite la propriété de Pythagore dans le triangle SOA.
SA2 = OA2 + SO2 = (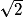
)2 + 72 = 51
donc SA = 7,1.
SA2 = OA2 + SO2 = (
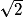)2 + 72 = 51donc SA = 7,1.
Exercice n°1
 |
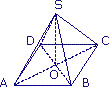Soit une pyramide régulière de base carrée ABCD et de hauteur [SO].
On connaît AB et SO. On veut calculer la longueur de l'arête [SA].
Remets les étapes dans l'ordre.
On connaît AB et SO. On veut calculer la longueur de l'arête [SA].
Remets les étapes dans l'ordre.
Faites glisser les étiquettes dans les zones prévues à cet effet.
4
3
1
2
On applique la propriété de Pythagore au triangle SOA rectangle en O.
→
→
imcAnswer1?
On applique la propriété de Pythagore au triangle ABC rectangle en B.
→
→
imcAnswer2?
On en déduit la valeur de AC, puis celle de OA.
→
→
imcAnswer3?
On en déduit la valeur de SA.
→
→
imcAnswer4?
Exercice n°2
La pyramide de Khéops a une base carrée de 230 m de côté et une hauteur de 138 m.
Calcule la mesure de son arête.
Calcule la mesure de son arête.
Écrivez les réponses dans les zones colorées.
1. La demi-diagonale de la base carrée mesure :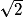 
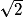m.
m. 2. À 1 m près par défaut, l'arête a donc pour mesure : m.
1. La demi-diagonale mesure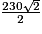 
, soit 115
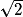m.
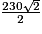, soit 115 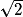m. 2. On applique la propriété de Pythagore :
a2 = 1382 + (115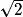
) = 45 494 ;
a = 213.
a2 = 1382 + (115
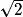) = 45 494 ;a = 213.
Exercice n°3
On considère une pyramide qui a une hauteur de 8 m et dont la base est un hexagone régulier de côté 6 m.
Calcule la mesure de son arête.
Calcule la mesure de son arête.
Écrivez les réponses dans les zones colorées.
a. Quelle est la distance entre le centre de l'hexagone et chacun des six sommets de cet hexagone ?
Réponse = m
Réponse = m
b. Combien mesure l'arête de la pyramide ?
Réponse = m
Réponse = m
a. Pense qu'un hexagone régulier peut se décomposer en 6 triangles équilatéraux.
b. L'arête de la pyramide est l'hypoténuse d'un triangle rectangle ayant, pour côtés de l'angle droit, la hauteur de la pyramide et le rayon du cercle circonscrit à l'hexagone de base.
a. L'hexagone régulier peut se décomposer en six triangles équilatéraux de côté 6 m.
b. On applique la propriété de Pythagore :
a2 = 82 + 62 = 100 ;
a = 10.
a2 = 82 + 62 = 100 ;
a = 10.
Exercice n°4
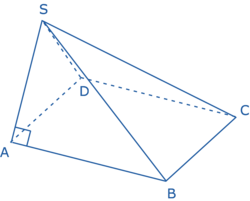
Soit SABCD une pyramide de base rectangulaire avec AB = 5, BC = 3 et AS = 4.
Calcule SD.
Calcule SD.
 |
Écrivez les réponses dans les zones colorées.
La pyramide SABCD est une pyramide régulière de base rectangulaire donc la droite (AS) est à la droite (AD).
Le triangle SAD est en A.
D'après le théorème de appliqué au triangle ASD rectangle en A, on a :
2 = 2 + AD2.
Or ABCD est un rectangle donc AD = .
D'après le théorème de appliqué au triangle ASD rectangle en A, on a :
2 = 2 + AD2.
Or ABCD est un rectangle donc AD = .
D'où SD2 = 42 + 32 = .
SD est une distance donc SD > 0
Conclusion SD = .
SD est une distance donc SD > 0
Conclusion SD = .
